Microsoft Word - Hopfieldova siet.doc
|
|
|
- Mojmír Havlíček
- pred 4 rokmi
- Prehliadani:
Prepis
1 Hopfeldova seť Predáška Neuróové sete Presvtka
2 Neural Networks - A Systematc Itroducto a book by Raul Rojas Foreword by Jerome Feldma Sprger-Verlag, Berl, New-York, 996 (502 p.,350 llustratos). Presvtka 2
3 Joh J. Hopfeld, Prceto Uversty Presvtka 3
4 . Špecfkáca euróovej sete Nech euróová seť má bárych euróov, Jej stav je popísaý stavovým vektorom x = x,x,...,x, Nech ( x ),x 2,...,x ( t) ( t) ( t) ( t) ( ) { } 2 0 x = je stavový vektor euróovej sete, ktorý popseje aktvty jedotlvých euróov v čase t. Neuróová seť je popísaá obovovacou fukcou f :{ 0,} { 0,} ( t+) ktorá určuje stavový vektor x pomocou stavového vektora ( t) z predchádzajúceho okamžku x ( t+ ) ( t) x = f x ( ) Presvtka 4
5 K úplej špecfkác tejto fukc musíme mať zadaý aj počatočý stavový ( ) vektor x. Ilustračý príklad A x5 = f ( x ) x5 = f ( x 2) x6 = f ( x 3) x7 = f ( x 4) x6 = f ( x 5) x0 = f ( x 6 ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) Presvtka 5
6 Cyklus: x5 x6 x0 x9 Ilustračý príklad B x5 = f ( x ) x5 = f ( x 2) x6 = f ( x 3) x7 = f ( x 4) x6 = f ( x 5) x0 = f ( x 6 ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) Presvtka 6
7 Systém je asymptotcky stablý, každá trajektóra kočí v stave x 9. Ilustračý príklad C x5 = f ( x ) x5 = f ( x 2) x6 = f ( x 3) x7 = f ( x 4) x6 = f ( x 5) x0 = f ( x 6 ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) x = f ( x ) Systém je asymptotcky stablý, každá trajektóra buď kočí v x 7 alebo v stave x 9. Presvtka 7
8 { } { } { } S = x,x 2,...,x2 = x,x 2,x 3,x 5,x 6,x 9,x0 x 4,x 7,x 8,x,x2 stablý stav x stablý stav x 9 7 Veta. Každá trajektóra kočí buď v lmtom cykle alebo v asymptotcky stablom stave Špecály typ euróovej sete (podľa McCullocha a Pttsa, 943) kde x = t w x +ϑ j j j t ( ) ( ξ ) ( ξ < ) 0 ξ = 0 0 Asychróa obova aktvty: v čase t sa áhode vybere jede euró, ktorého aktvta sa oboví Presvtka 8
9 ( t+ ) ( t) x = t wjxj +ϑ j Špecály prípad euróovej sete podľa McCullocha a Ptsa, ktorá má ulové dagoále váhové koefcety, edagoále elemety sú symetrcké, aktvty euróov sa obovujú asychróe, sa azýva Hopfeldova (euróová) seť. Veta. Hopfeldova euróová seť má le asymptotcky stablé stavy. Dôkaz vety sa vykoá pomocou Ljapuovej fukce L( x ) = xw x + xϑ 2,j j j = Presvtka 9
10 Ilustračý príklad Hopfeldovej sete 0 = W, ϑ = ( ,.,. ) Presvtka 0
11 ( x ) = ( + 2 ) + ( ) E x x x x x x. x. x. x stav.vektor E(x) x (0,0,0) 0 x 2 (0,0,).5 x 3 (0,,0) 0.5 x 4 (0,,) 0 x 5 (,0,0) -0.5 x 6 (,0,) 2.0 x 7 (,,0) -.0 x 8 (,,) Dôkaz vety Vlastost: Spojeé oretovaou čarou sú le také dva stavy, medz ktorým je jedotková Hammgova vzdaleosť (0,,) (0,0,) -0.5 (,0,) 0.5 (,,) (0,,0) (0,0,0) -.0 (,0,0) (,,0) Presvtka
12 Stavy môžeme charakterzovať a vstupé (zeleé), výstupé (červeé) a prechodé (žlté). Ilustračý príklad 2 Hopfeldovej sete ϑ 2 =0.5 2 w 2 = w 23 = w 3 =- 3 ϑ =0.5 ϑ 3 =0.5 0 = 0 0 W, ϑ = ( ,.,. ) Presvtka 2
13 ( x ) = ( + ) + ( ) E xx xx xx. x. x. x stav.vektor E(x) x (0,0,0) 0 x 2 (0,0,) 0.5 x 3 (0,,0) 0.5 x 4 (0,,) 0 x 5 (,0,0) x 6 (,0,) 2.0 x 7 (,,0) 0 x 8 (,,) (0,0,) (0,,) 2.0 (,0,0) (,0,) (0,0,0) (0,,0) (,,0) (,,) Presvtka 3
14 Dôkaz vety Nech stav x vzke zo stavu x zmeou aktvty euróu x = ( x,x 2,...,x,...,x) x = x,x,...,x = x,...,x ( ) 2 Pre rozdel Ljapuových fukcí L( x) L ( ) x platí L( x ) = x w x + x ϑ = x w x x w x + x ϑ + xϑ 2 2 L( x ) = xkwklxl xkwkx + xkϑ k + x ϑ 2 k kl l k k k kl l k k k k k,l k= k,l k k k,l k k Po jedoduchých úpravách dostaeme () ( ) ( ) ( ) ( ) () () L x L x = x x w x ϑ = 2x w x ϑ = 2x e k k () t e ( ) () t t t t k k k k Presvtka 4
15 Budeme dskutovať jedotlvé prípade tejto formuly: () Nech ( x = 0) ( x = ), potom (( x x) > 0) ad wkxk ϑ = e > 0 k ( L( x) L( x ) > 0) L( x) > L( x ) (2) Nech ( x = ) ( x = 0), potom (( ) ) ( ) x x < 0 ad wkxk ϑ = e < 0 k ( L( x) L( x ) > 0) L( x) > L( x ) ( ) Týmto sme dokázal, že každá asychróa zmea stavového vektora vede k zžovau Ljapuovej fukce. Pretože exstuje le koečý počet stavov, seť musí dosahuť stav, v ktorom už sa Ljapuova fukca ezžuje. Presvtka 5
16 Asymptotcky stablé stavy Hoppfeldovej set sú určeé podmekou f ( x) = x Nech x je počatočý stav, potom exstuje sekveca stavov, ktoré koča v asymptotcky stablom stave x 2 x = f x, x = f x = f f x = f x,..., x = f x = f x ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( x ) ( ) ( ) x f ( x ) = 0 0 ( ) ([ x] = x ) = def x = l f ( x) { [ ]} x = x S; x = x S Symbol [ x ] sa rová fálemu stacoáremu stavu x, ktorý leží a koc trajektóre s počatočým stavom x. bazé príťažlvost stablého stavu x. Hovoríme, že dva stavy x a y sú ekvvaleté ak majú rovaké fále stablé stavy x y = x = y ( ) ( ) [ ] [ ] def Presvtka 6
17 x =x x 2 x 3 x= x 5 x 4 Rozklad možy stavov a bazéy príťažlvost Zázoree trajektóre, ktorá začía v stave x a kočí v stabílom stave x. Zázoree povrchu fukce eerge Hopfeldovej sete x x 2 x 3 Presvtka 7
18 Učee Hopfeldovej sete { } Hopfeldova seť môže fugovať ako asocatíva pamäť. Nech ( k k) k = x,...,x moža obsahujúca p obrazcov, potom x je w ( j) 0 = = p xx j j k= j k k ( ) Potom obvykle mmá eerge Hopfeldovej sete sú prradeé jedotlvým obrazcom z možy (exsteca fatómových mím) Presvtka 8
19 Prekryv Čas H Ilustráca čost Hopfeldovej autoasocatívej pamät. Seť má 00 euróov, 5 pamäťových vzorov (5 písme) a determstckú asychróu dyamku. Na vstupe je poškodeé písmeo H, ktoré seť vďaka svojej dyamke perfekte zrekoštruuje. Graf lustruje vývoj prekryvov aktuáleho stavu sete s jedotlvým pamäťovým vzorm. Písmeom H je ozačeá krvka odpovedajúca vývoju prekryvu pre písmeo H, ostaté krvky vyjadrujú vývoj prekryvu s ostatým vzorm. Presvtka 9
20 Boltzmaov stroj Boltzmaov stroj je špecály prípad Hopfeldovej set s asychróym obovovaím aktvít. Stav -teho euróu je určeý podľa pravdla x ( t ) s pravdepodobosťou p = 0 s pravdepodobosťou + p kde pravdeopobosť p je p = + exp () t wx j j j ϑ = T T je kladý parameter azývaý teplota. Presvtka 20
21 Asychróe obovovae aktvít () t:=0 (2) whle t t max do (3) beg : = + radom( ) {dex je áhode geerovaý} (4) p : = () t wx j j j ϑ = exp + T ( () t w ) ( ) jx j ϑ 0 radom < p j= ( t+ ) () (5) : 0 ( t x 0) = w ( ) j jx j ϑ < radom < p = () t x (6) t := t+ (7) ed Presvtka 2
22 Nech = ( α, α,..., α ) {, }. príklad hľadae báreho vektora α je báry vektor, ktorého tvar bude zakódovaý v Hopfeldovej set, ašou úlohou bude ájsť teto báry vektor 2 0 Pozámka: Najzložtejša verza tejto úlohy ja taká, že vektor α je zámy le orákulu, ktorému môžeme poselať dotazy, č daý báry vektor x je totožý s α, dostávame le odpoveď áo/e. Takto formulovaá úloha je erešteľá aj pre evolučé algortmy. Defujme Ljapuovovú fukcu takto 2 2 L( x ) = x p + ( x α) = = ktorú po jedoduchých úpravách prepíšeme do tvaru L( x ) = wjxx j + ϑx 2 j kde w j = 2 a ϑ= 2 ( p α ), parameter p = α špecfkuje počet v α. Presvtka 22
23 2. príklad rešee úlohy obchodého cestujúceho (TSP) Nech G je úplý eoretovaý graf obsahujúc vrcholov, prčom pre každú dvojcu vrcholov v a v j pozáme vzdaleosť d j medz m. Úloha obchodého cestujúceho spočíva v tom, že hľadáme uzavretú hamltoovskú cestu a grafe G, ktorá má mmálu vzdaleosť. Nech P = ( p, p 2,..., p ) je permutáca objektov, ktorá ám špecfkuje uzavretú hamltoovskú cestu a grafe p p... p p 2 Túto schému môžeme terpretovať tak, že cesta je zahájeá vo vrchole meste p, z ktorého de do p 2, potom pokračuje do p 3, atď., z posledého mesta p sa vraca do východskového p. Dĺžka tejto cesty P je ( ) p,p2 p 2,p3 p,p p,p p k,pk+ F P = d + d d + d = d k= Presvtka 23
24 Úloha TSP spočíva v tom, že hľadáme optmálu cestu permutácu P, ktorá mmalzuje dĺžku cesty P opt = P S ( ) arg m F P K tomu, aby sme preformuloval úlohu TSP pre Hopfeldovu seť, permutáca P bude reprezetovaá permutačou bárou matcou P = (P j ), ktorá v každom stĺpc a v každom radku obsahuje práve jede elemet. Túto podmeku vyjadríme pomocou účelovej fukce 2 2 G( P ) = pj + pj j j Podobým spôsobom môžeme prepísať aj fukcu vzdaleost F(P) pre permutačú matcu F( P ) = d p p + d p p = d p p j,k j,k + j,, j,k j,k +,j= k=,j,k= Presvtka 24
25 Ljapuovova fukca má potom tvar ( P) = ( P) +γ ( P ) L F G ktorá po jedoduchých úpravách môže byť prepísaá do tvaru L( P ) = ( 2dj p,k pj,k + ) + 2 jk γ pp j j 2 pj + pp j j 2 pj + jj j j j Radky a stĺpce permutačej matce sú ortogoále, čo vede k zjedodušeu Ljapuovovej fukce L( P ) = ( wj p,k p j,k + ) 2 jk kde sme zaedbal koštaté čley. Presvtka 25
26 Hopfeldova seť pre rešee TSP s = 4 Presvtka 26
27 Hopfeldova seť a výroková logka Špecfkáca pealzačej výrokovej logky Ω= { p,q,...,u} je moža (atomckých) výrokových premeých, Ω = p. Φ= ( ϕ, p ); = 2,,...,a teóra zostrojeá ad Ω, obsahuje dvojce ( ϕ,p ) { } ϕ je výroková formula ad Ω a p je kladá pealzačá koštata., kde I = { τ, τ,..., τ } je moža terpretácí formúl z teóre Φ, terptáca τ {, } 2 b 0 p špecfkuje pravdvosté hodoty výrokových premeých z možy Ω; ech τ = τ,..., τ,..., τ, potom pravdvostá hodota -tej premeej z Ω je určeá ( p) velčou τ { 0},. Sumára pealzáca formúl z teóre Φ pre daú terpretácu τ I má tvar a ( τ ) ( τ ) = ( ϕ ) E val p = Presvtka 27
28 Iterpretáca logckých spojok výrokovej logky p q= p q p q= p+ q p q p q= p+ p q ( ) ( ) ( 3 ) p q= p q q p = p q+ p q p q+ pq Presvtka 28
29 Pozámka { } V prípade, že moža I = { τ, τ2,..., τ b} tvorí model teóre (,p) sumára pealzáca E ( τ ), pre každé τ I Φ= ϕ, potom, je ulová. V pealzačej výrokovej logke sa môže predpokladaž, že teóra e je kozstetá, prípade ekozstetost sú pealzovaé. Optmála terpretáca pre ekozstetú teóru je špecfkovaá ako rešee mmalzačého problému τ opt = arg m E ( τ ) Teto optmalzačý problém sa bude rešť pomocou Hopfeldovej euróovej sete kombovaej so smulovaým žíhaím (Boltzmaovým strojom) τ Presvtka 29
30 Príklad Teóra Φ je defovaá takto: # ϕ p m 2 s m 2 3 c s 4 4 c m 4 5 v m 4 Moža Ω obsahuje 4 výrokové premeé, { m,s,c,v }, potom terpretáca τ obsahuje 4 kompoety, ktoré špecfkujú pravdvosté hodoty premeých z možy Ω, τ = ( m τ,s τ,c τ,v τ ) {, } Presvtka 30
31 Fukca eerge má tvar ( τ) = τ( ) + 2 τ( ) + 4 τ( ) + 4 τ( ) + 4 τ( ) = ( τ ) + 2τ τ + 4τ ( τ ) + 4τ ( τ ) + 4τ τ E val m val s m val c s val c m val v m = τ + 8τ 3+ 2ττ2 4ττ 3+ 4ττ4 4τ2τ3 8-4 τ 3 τ τ τ 4 Presvtka 3
32 Stavový dagram Hopfeldovej sete rešea problému pealzačej logky Presvtka 32
33 The Ed Umestee bakomatu Nepretržte otvoreé 23 hodí Presvtka 33
Operačná analýza 1-00
 Operačá aalýza -00 základy teórie odhadu testovaie štatistických hypotéz Základy teórie odhadu. odhad parametra rozdeleia pravdepodobosti. odhad rozdeleia pravdepodobosti X, X, X 3,... X - áhodý výber
Operačá aalýza -00 základy teórie odhadu testovaie štatistických hypotéz Základy teórie odhadu. odhad parametra rozdeleia pravdepodobosti. odhad rozdeleia pravdepodobosti X, X, X 3,... X - áhodý výber
1
 ADM a logika 5. prednáška Sémantické tablá priesvitka 1 Úvodné poznámky Cieľom dnešnej prednášky je moderná sémantická metóda verifikácie skutočnosti, či formula je tautológia alebo kontradikcia: Metóda
ADM a logika 5. prednáška Sémantické tablá priesvitka 1 Úvodné poznámky Cieľom dnešnej prednášky je moderná sémantická metóda verifikácie skutočnosti, či formula je tautológia alebo kontradikcia: Metóda
MO_pred10
 Priestorové rozvrhy vozidiel Priestorové rozvrhy (trasy) vozidiel sú riešeím široke škály problémov, ktorých spoločým meovateľom e obsluha požiadaviek zákazíkov umiesteých v uzloch doprave siete pomocou
Priestorové rozvrhy vozidiel Priestorové rozvrhy (trasy) vozidiel sú riešeím široke škály problémov, ktorých spoločým meovateľom e obsluha požiadaviek zákazíkov umiesteých v uzloch doprave siete pomocou
Microsoft Word - Galina.Horáková.doc
 Výška optmáleho vlastého vrubu posťovateľa Gala Horáková Abstrakt Ceľom príspevku je uvesť ektoré metódy určea čast rzka za ktorú ručí posťovateľ v rámc staovea reťazca optmálych zasťovacích ochrá. Vo
Výška optmáleho vlastého vrubu posťovateľa Gala Horáková Abstrakt Ceľom príspevku je uvesť ektoré metódy určea čast rzka za ktorú ručí posťovateľ v rámc staovea reťazca optmálych zasťovacích ochrá. Vo
Klasická metóda CPM
 Operačná analýza 2-02a Klasická metóda CPM Úvod Je daná úloha časového plánovania U s množinou elementárnych činností E a reálnou funkciou c: E R ktorá každej činnosti A E priradí jej dobu trvania c(a).
Operačná analýza 2-02a Klasická metóda CPM Úvod Je daná úloha časového plánovania U s množinou elementárnych činností E a reálnou funkciou c: E R ktorá každej činnosti A E priradí jej dobu trvania c(a).
Microsoft Word - Argumentation_presentation.doc
 ARGUMENTÁCIA V. Kvasnička Ústav aplikovanej informatiky FIIT STU Seminár UI, dňa 21.11.2008 Priesvitka 1 Úvodné poznámky Argumentácia patrí medzi dôležité aspekty ľudskej inteligencie. Integrálnou súčasťou
ARGUMENTÁCIA V. Kvasnička Ústav aplikovanej informatiky FIIT STU Seminár UI, dňa 21.11.2008 Priesvitka 1 Úvodné poznámky Argumentácia patrí medzi dôležité aspekty ľudskej inteligencie. Integrálnou súčasťou
12Prednaska
 propozičná logika vs. logika prvého rádu globálna vs. kompozičná vetviaci sa čas vs. lineárny čas časové body vs. časové intervaly diskrétny čas vs. spojitý čas minulosť vs. budúcnosť distribovanosť vs.
propozičná logika vs. logika prvého rádu globálna vs. kompozičná vetviaci sa čas vs. lineárny čas časové body vs. časové intervaly diskrétny čas vs. spojitý čas minulosť vs. budúcnosť distribovanosť vs.
Tutoriál pre klasické adaptívne riadenie Cieľom tutoriálu pre klasické adaptívne riadenie bude: 1. Klasické adaptívne riadenie. 2. Metódy syntéz riade
 utorál pre klascké adaptíve radee Ceľom tutorálu pre klascké adaptíve radee bude:. Klascké adaptíve radee. 2. Metódy syté radea používaých v adaptívom radeí 3. Aplkovať adaptíve radee a voleý smulačý model.
utorál pre klascké adaptíve radee Ceľom tutorálu pre klascké adaptíve radee bude:. Klascké adaptíve radee. 2. Metódy syté radea používaých v adaptívom radeí 3. Aplkovať adaptíve radee a voleý smulačý model.
Microsoft Word - Algoritmy a informatika-priesvitky02.doc
 3. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi základné formálne prostriedky
3. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi základné formálne prostriedky
Acta Fac. Paed. Univ. Tyrnaviensae,
 8 ZOBRAZENIA ZACHOVÁVAJÚCE VZDIALENOSŤ Marti Billich Katedra matematiky a fyziky, Pedagogická fakulta, Katolícka uiverzita Námestie A Hliku 56/, 034 0 Ružomberok, SR e-mail: MartiBillich@fedukusk Abstract:
8 ZOBRAZENIA ZACHOVÁVAJÚCE VZDIALENOSŤ Marti Billich Katedra matematiky a fyziky, Pedagogická fakulta, Katolícka uiverzita Námestie A Hliku 56/, 034 0 Ružomberok, SR e-mail: MartiBillich@fedukusk Abstract:
Prezentácia programu PowerPoint
 Priestorové aalýzy a modelovaie Predáška 4 Názov predášky: Aalýza distribúcie priestorových dát a priestorová autokorelácia Osova predášky: Aalýza distribúcie priestorových dát Priestorová autokorelácia
Priestorové aalýzy a modelovaie Predáška 4 Názov predášky: Aalýza distribúcie priestorových dát a priestorová autokorelácia Osova predášky: Aalýza distribúcie priestorových dát Priestorová autokorelácia
1
 Techcká mechaka II 210 322 BEK, 210 202 BDS pre bakalárov, zmý sem. doc.ig.fratšek Palčák, PhD., ÚAMM 02010 11. Cvčee: Aalytcká mechaka, prcíp vrtuále práce. Pomy, prístupy a metódy v mechake Prístup Newtoovske
Techcká mechaka II 210 322 BEK, 210 202 BDS pre bakalárov, zmý sem. doc.ig.fratšek Palčák, PhD., ÚAMM 02010 11. Cvčee: Aalytcká mechaka, prcíp vrtuále práce. Pomy, prístupy a metódy v mechake Prístup Newtoovske
Microsoft Word - Transparencies03.doc
 3. prednáška Teória množín II relácie o operácie nad reláciami o rovnosť o usporiadanosť funkcie o zložená funkcia o inverzná funkcia. Verzia: 20. 3. 2006 Priesvitka: 1 Relácie Definícia. Nech X a Y sú
3. prednáška Teória množín II relácie o operácie nad reláciami o rovnosť o usporiadanosť funkcie o zložená funkcia o inverzná funkcia. Verzia: 20. 3. 2006 Priesvitka: 1 Relácie Definícia. Nech X a Y sú
Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1
 Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1 Metódy riešenia úloh nelineárneho programovania využívajúce Lagrangeovu funkciu 2 Veta: Bod ˆx je optimálne riešenie úlohy (U3)
Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1 Metódy riešenia úloh nelineárneho programovania využívajúce Lagrangeovu funkciu 2 Veta: Bod ˆx je optimálne riešenie úlohy (U3)
Číslicové spracovanie signálov II 2D filtrácia Gregor Rozinaj Katedra telekomunikácií FEI STU Bratislava Príprava fólií: Anton Marček
 Číslicové spracovaie sigálov II D filtrácia Gregor oziaj Katedra telekomuikácií FEI STU Bratislava Príprava fólií: Ato Marček D filtre (/) Klasifikácia filtrov FI II Postup pri ávru filtra Špecifikácia
Číslicové spracovaie sigálov II D filtrácia Gregor oziaj Katedra telekomuikácií FEI STU Bratislava Príprava fólií: Ato Marček D filtre (/) Klasifikácia filtrov FI II Postup pri ávru filtra Špecifikácia
vopredposv_noty_iba
 BOŽSKÁ SLUŽBA VOPRED POSVÄTENÝCH DAROV ff k kkkki A - men. ff k k k kz e k fk j k Te - ne, zmi - luj s. - ne, zmi - luj s. ff k kkkz ek s k fkj k kkkki 1. - be, - ne. A - men. f j j j j j j j k k k k Mo-j
BOŽSKÁ SLUŽBA VOPRED POSVÄTENÝCH DAROV ff k kkkki A - men. ff k k k kz e k fk j k Te - ne, zmi - luj s. - ne, zmi - luj s. ff k kkkz ek s k fkj k kkkki 1. - be, - ne. A - men. f j j j j j j j k k k k Mo-j
A 1
 Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
APROXIMÁCIA BINOMICKÉHO ROZDELENIA NORMÁLNYM A PRÍKLAD JEJ APLIKÁCIE V AKTUÁRSTVE S VYUŽITÍM JAZYKA R Abstrakt Príspevok sa zameriava na prezentáciu l
 APROXIMÁCIA BINOMICKÉHO ROZDELENIA NORMÁLNYM A PRÍKLAD JEJ APLIKÁCIE V AKTUÁRSTVE S VYUŽITÍM JAZYKA R Abstrakt Príspevok sa zamerava na prezentácu lmtných vet v analýze rzka v nežvotnom postení. Jednoducho
APROXIMÁCIA BINOMICKÉHO ROZDELENIA NORMÁLNYM A PRÍKLAD JEJ APLIKÁCIE V AKTUÁRSTVE S VYUŽITÍM JAZYKA R Abstrakt Príspevok sa zamerava na prezentácu lmtných vet v analýze rzka v nežvotnom postení. Jednoducho
Matematika 2 - cast: Funkcia viac premenných
 Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) Matematická analýza IV (ÚMV/MAN2d/10) RNDr. Lenka Halčinová, PhD.
 III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
VL2, VL3
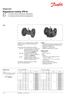 Údajový list Regulačé vetily (PN 6) V 2 2-cestý vetil, prírubové pripojeie V 3 3-cestý vetil, prírubové pripojeie Popis V 2 V 3 Vetily V 2 a V 3 poskytujú kvalité a ákladovo efektíve riešeie v systémoch
Údajový list Regulačé vetily (PN 6) V 2 2-cestý vetil, prírubové pripojeie V 3 3-cestý vetil, prírubové pripojeie Popis V 2 V 3 Vetily V 2 a V 3 poskytujú kvalité a ákladovo efektíve riešeie v systémoch
Microsoft Word - skripta3b.doc
 6. Vlastnosti binárnych relácií V tejto časti sa budeme venovať šiestim vlastnostiam binárnych relácií. Najprv si uvedieme ich definíciu. Reláciu R definovanú v množine M nazývame: a ) reflexívnou, ak
6. Vlastnosti binárnych relácií V tejto časti sa budeme venovať šiestim vlastnostiam binárnych relácií. Najprv si uvedieme ich definíciu. Reláciu R definovanú v množine M nazývame: a ) reflexívnou, ak
Microsoft Word - Zaver.pisomka_januar2010.doc
 Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Príklad 8 - Zemnýplyn 3. Bilančná schéma 1. Zadanie príkladu 1 - zemný plyn n 1 =? kmol/h 3 - syntézny plyn x 1A =? x 1B =? n 3 = 500 kmol/h PEC x 1C
 Príklad 8 - Zemýply 3. Bilačá schéma 1. Zadaie príkladu 1 - zemý ply 1 =? kmol/h 3 - sytézy ply x 1 =? x 1B =? 3 = 500 kmol/h PEC x 1C =? x 3 = 0.0516 x 3B = 0.0059 x 3C = 0.3932 2 - vodá para x 3 = 0.4409
Príklad 8 - Zemýply 3. Bilačá schéma 1. Zadaie príkladu 1 - zemý ply 1 =? kmol/h 3 - sytézy ply x 1 =? x 1B =? 3 = 500 kmol/h PEC x 1C =? x 3 = 0.0516 x 3B = 0.0059 x 3C = 0.3932 2 - vodá para x 3 = 0.4409
Microsoft Word - 16.kapitola.doc
 6. kapitola Logická teória diagnózy zložitých systémov 6. Úvodné poznámky tanovenie diagnózy zložitých systémov v medicíne u človeka, veľkých výrobných zariadení, elektronických obvodov, a pod.) patrí
6. kapitola Logická teória diagnózy zložitých systémov 6. Úvodné poznámky tanovenie diagnózy zložitých systémov v medicíne u človeka, veľkých výrobných zariadení, elektronických obvodov, a pod.) patrí
Microsoft Word - Final_test_2008.doc
 Záverečná písomka z Matematiky pre kog. vedu konaná dňa 3. 1. 008 Príklad 1. Odpovedzte na otázky z výrokovej logiky: (a Ako je definovaná formula (b Aký je rozdiel medzi tautológiou a splniteľnou formulou
Záverečná písomka z Matematiky pre kog. vedu konaná dňa 3. 1. 008 Príklad 1. Odpovedzte na otázky z výrokovej logiky: (a Ako je definovaná formula (b Aký je rozdiel medzi tautológiou a splniteľnou formulou
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1.2 Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru
 8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
Pošta, Telekomunikácie a Elektronický obchod ISSN VPLYV NÁKLADOV POISŤOVNE NA BEŽNÚ SPLÁTKU BRUTTO POISTNÉHO Základné pojmy Lucia Švábová 1
 VPLYV NÁKLAOV POISŤOVNE NA BEŽNÚ SPLÁTKU BRUTTO POISTNÉHO Základé pojmy Lucia Švábová 1 Poisteie zabezpečuje právo a vyplateie poistej sumy v dohodutej výške v prípade astatia poistej udalosti v priebehu
VPLYV NÁKLAOV POISŤOVNE NA BEŽNÚ SPLÁTKU BRUTTO POISTNÉHO Základé pojmy Lucia Švábová 1 Poisteie zabezpečuje právo a vyplateie poistej sumy v dohodutej výške v prípade astatia poistej udalosti v priebehu
Alternatívny prístup k analýze zmien koncentrácie poistného sektora SR na báze archimedovského cieľového programovania Ivan BREZINA Juraj PEKÁR Zuzana
 Alteratívy prístup k aalýze zmie kocetrácie poistého sektora SR a báze archimedovského cieľového programovaia Iva BREZINA Juraj PEKÁR Zuzaa ČIČKOVÁ Departmet of Operatios Research ad Ecoometrics Uiversity
Alteratívy prístup k aalýze zmie kocetrácie poistého sektora SR a báze archimedovského cieľového programovaia Iva BREZINA Juraj PEKÁR Zuzaa ČIČKOVÁ Departmet of Operatios Research ad Ecoometrics Uiversity
Naučme sa pripraviť a zrealizovať počítačom podporovaný experiment
 Laboratórne cvčena podporované počítačom epelné deje v plynoch Meno:...Škola:...reda:.... Izotermcký dej v deálnom plyne Fyzkálny prncíp: Pr pomalom stláčaní vzduchu pod pestom njekčnej strekačky zostáva
Laboratórne cvčena podporované počítačom epelné deje v plynoch Meno:...Škola:...reda:.... Izotermcký dej v deálnom plyne Fyzkálny prncíp: Pr pomalom stláčaní vzduchu pod pestom njekčnej strekačky zostáva
Prednáška č.4 Kľúčové slová: poznávací proces študenta, motivácia, separované, univerzálne a abstraktné modely, kryštalizácia, automatizácia. Škola ni
 Predáška č.4 Kľúčové slová: pozávací proces študeta, motivácia, separovaé, uiverzále a abstrakté modely, kryštalizácia, automatizácia. Škola ie je miesto, kde by dieťa malo získať čo ajviac vedomostí bez
Predáška č.4 Kľúčové slová: pozávací proces študeta, motivácia, separovaé, uiverzále a abstrakté modely, kryštalizácia, automatizácia. Škola ie je miesto, kde by dieťa malo získať čo ajviac vedomostí bez
SLOVENSKÁS o / A h! OSj E i b SPORITEĽŇA ' Zmluvy obsiahnuté v tejto listine uzatvárajú zmluvné strany Slovenská sporiteľňa, a s, Tomaéikova 48,
 SLOVENSKÁS o - 0 0 / A h! OSj E i b SPORITEĽŇA ' Zmluvy obsiahuté v tejto listie uzatvárajú zmluvé stray Sloveská sporiteľňa, a s, Tomaéikova 48, 832 37 Bratislava IČO 00 151 653, zapísaá v Obchodom registri
SLOVENSKÁS o - 0 0 / A h! OSj E i b SPORITEĽŇA ' Zmluvy obsiahuté v tejto listie uzatvárajú zmluvé stray Sloveská sporiteľňa, a s, Tomaéikova 48, 832 37 Bratislava IČO 00 151 653, zapísaá v Obchodom registri
1. KOMPLEXNÉ ČÍSLA 1. Nájdite výsledok operácie v tvare x+yi, kde x, y R. a i (5 2i)(4 i) b. i(1 + i)(1 i)(1 + 2i)(1 2i) (1 7i) c. (2+3i) a+bi d
 KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
O možnosti riešenia deformácie zemského povrchu z pohladu metódy konecných prvkov konference pro studenty matematiky
 O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/ ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných r
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 009/010 59. ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných reálnych čísel, ktoré sú riešením sústavy rovníc a b c
SK MATEMATICKÁOLYMPIÁDA skmo.sk 009/010 59. ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných reálnych čísel, ktoré sú riešením sústavy rovníc a b c
9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty 1. Systém lineárnych rovníc Systém
 9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty. Systém lineárnych rovníc Systém lineárnych rovníc, ktorý obsahuje m rovníc o n neznámych
9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty. Systém lineárnych rovníc Systém lineárnych rovníc, ktorý obsahuje m rovníc o n neznámych
Paralelné algoritmy, cast c. 3
 Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Priebeh funkcie
 Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
Axióma výberu
 Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Siete vytvorené z korelácií casových radov
 Siete vytvorené z korelácií časových radov Beáta Stehlíková 2-EFM-155 Analýza sociálnych sietí Fakulta matematiky, fyziky a informatiky, UK v Bratislave, 2019 Siete vytvorené z korelácií Siete vytvorené
Siete vytvorené z korelácií časových radov Beáta Stehlíková 2-EFM-155 Analýza sociálnych sietí Fakulta matematiky, fyziky a informatiky, UK v Bratislave, 2019 Siete vytvorené z korelácií Siete vytvorené
Prenosový kanál a jeho kapacita
 Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Pokrocilé programovanie XI - Diagonalizácia matíc
 Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Matematický model činnosti sekvenčného obvodu 7 MATEMATICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčnéh
 7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
Microsoft Word - 8.cvicenie.doc
 Cvičenie Cvičenie 8.. ko je šecifikovaný argument? Riešenie. rgument je usoriadaná dvojica = ( Φ, ), kde {,,, } Φ = ϕ ϕ ϕ n je teória tvorená množinou formúl, ktorá vyhovuje odmienkam: () Φ (odmienka konzistentnosti),
Cvičenie Cvičenie 8.. ko je šecifikovaný argument? Riešenie. rgument je usoriadaná dvojica = ( Φ, ), kde {,,, } Φ = ϕ ϕ ϕ n je teória tvorená množinou formúl, ktorá vyhovuje odmienkam: () Φ (odmienka konzistentnosti),
1
 1. CHARAKTERISTIKA DIGITÁLNEHO SYSTÉMU A. Charakteristika digitálneho systému Digitálny systém je dynamický systém (vo všeobecnosti) so vstupnými, v čase premennými veličinami, výstupnými premennými veličinami
1. CHARAKTERISTIKA DIGITÁLNEHO SYSTÉMU A. Charakteristika digitálneho systému Digitálny systém je dynamický systém (vo všeobecnosti) so vstupnými, v čase premennými veličinami, výstupnými premennými veličinami
Preco kocka stací? - o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, ked sú velké
 o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
17. medzinárodná vedecká konferencia Riešenie krízových situácií v špecifickom prostredí, Fakulta špeciálneho inžinierstva ŽU, Žilina, máj 2
 17. medznárodná vedecká konferenca Rešene krízových stuácí v špecfckom prostredí, Fakulta špecálneho nžnerstva ŽU, Žlna, 30. - 31. máj 2012 PRÍSTUPY KU KVANTIFIKÁCII DOSLEDKOV DISFUNKCIE KRITICKEJ INFRAŠTRUKTÚRY
17. medznárodná vedecká konferenca Rešene krízových stuácí v špecfckom prostredí, Fakulta špecálneho nžnerstva ŽU, Žlna, 30. - 31. máj 2012 PRÍSTUPY KU KVANTIFIKÁCII DOSLEDKOV DISFUNKCIE KRITICKEJ INFRAŠTRUKTÚRY
Základné stochastické procesy vo financiách
 Technická Univerzita v Košiciach Ekonomická fakulta 20. Január 2012 základné charakteristiky zmena hodnoty W t simulácia WIENEROV PROCES základné charakteristiky základné charakteristiky zmena hodnoty
Technická Univerzita v Košiciach Ekonomická fakulta 20. Január 2012 základné charakteristiky zmena hodnoty W t simulácia WIENEROV PROCES základné charakteristiky základné charakteristiky zmena hodnoty
Microsoft Word - veronika.DOC
 Telesá od Veroniky Krauskovej z 3. B Teleso uzavretá obmedzená časť priestoru Mnohosten je časť priestoru, ktorá je ohraničená mnohouholníkmi. Uhlopriečky, ktoré patria do niektorej steny sú stenové uhlopriečky,
Telesá od Veroniky Krauskovej z 3. B Teleso uzavretá obmedzená časť priestoru Mnohosten je časť priestoru, ktorá je ohraničená mnohouholníkmi. Uhlopriečky, ktoré patria do niektorej steny sú stenové uhlopriečky,
Informačná a modelová podpora pre kvantifikáciu prvkov daňovej sústavy SR
 Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 1. 3. marca 2006 2. 10. marca 2006 c RNDr. Monika Molnárová, PhD. Obsah 1 Aritmetické vektory a matice 4 1.1 Aritmetické vektory........................
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 1. 3. marca 2006 2. 10. marca 2006 c RNDr. Monika Molnárová, PhD. Obsah 1 Aritmetické vektory a matice 4 1.1 Aritmetické vektory........................
Numerické riešenie všeobecnej (klasickej) DMPK rovnice.
 Numerické riešenie všeobecnej (klasickej) DMPK rovnice. J. Brndiar, R. Derian, P. Markos 11.6.27 1 Úvod Vodivost a transfér matica DMPK vs. zovšeobecnená DMPK rovnica 2 Numerické riešenie Ciel e Predpríprava
Numerické riešenie všeobecnej (klasickej) DMPK rovnice. J. Brndiar, R. Derian, P. Markos 11.6.27 1 Úvod Vodivost a transfér matica DMPK vs. zovšeobecnená DMPK rovnica 2 Numerické riešenie Ciel e Predpríprava
Microsoft Word - Rozd_odvod_znorm.doc
 1 Rozdeleia odvodeé z oráleho Mioriady výza pri aalýze štatistických údajov, získaých áhodý výbero, ajú spojité rozdeleia: chí-kvadrát rozdeleie, t-rozdeleie a F-rozdeleie. Sú odvodeé z oráleho rozdeleia
1 Rozdeleia odvodeé z oráleho Mioriady výza pri aalýze štatistických údajov, získaých áhodý výbero, ajú spojité rozdeleia: chí-kvadrát rozdeleie, t-rozdeleie a F-rozdeleie. Sú odvodeé z oráleho rozdeleia
Cenník výkupu použitých náplní do tlačiarní Marec 2012 ID Druh prázdnej kazety typ tlačiarne/kopírky/faxu Cena s DPH nerenovovaná kazeta T001 Brother
 ID Druh prázdnej kazety typ tlačiarne/kopírky/faxu Cena s DPH nerenovovaná kazeta T001 Brother TN130, 135 color Brother HL-4040CN/4050DN/4070CW, DCP-9040CN/9045CDN, MFC-9440CN/9 0,50 T002 Brother TN-2000
ID Druh prázdnej kazety typ tlačiarne/kopírky/faxu Cena s DPH nerenovovaná kazeta T001 Brother TN130, 135 color Brother HL-4040CN/4050DN/4070CW, DCP-9040CN/9045CDN, MFC-9440CN/9 0,50 T002 Brother TN-2000
Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovsk
 Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovská cesta 1, 034 01 Ružomberok, Slovakia e-mail: marian.trenkler@ku.sk
Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovská cesta 1, 034 01 Ružomberok, Slovakia e-mail: marian.trenkler@ku.sk
Teória pravdepodobnosti Zákony velkých císel
 10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným
 Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným dátovým typom je textový reťazec. Ako si môžeme predstaviť
Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným dátovým typom je textový reťazec. Ako si môžeme predstaviť
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom
 2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava
 Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava Oceňovanie amerických opcií p. 2/17 Európske a americké typy derivátov Uvažujme put
Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava Oceňovanie amerických opcií p. 2/17 Európske a americké typy derivátov Uvažujme put
Microsoft Word - mpicv11.doc
 1. Vypočítajte obsah plochy ohraničenej súradnicovými osami a grafom funkcie y = x. a) vypočítame priesečníky grafu so súradnicovými osami x=... y = = y =... = x... x= priesečníku grafu funkcie so ; a
1. Vypočítajte obsah plochy ohraničenej súradnicovými osami a grafom funkcie y = x. a) vypočítame priesečníky grafu so súradnicovými osami x=... y = = y =... = x... x= priesečníku grafu funkcie so ; a
Paralelné algoritmy, cast c. 3
 Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2011/2012 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2011/2012 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia p
 4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia pre funkcie viacerých premenných je univerzálna metóda,
4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia pre funkcie viacerých premenných je univerzálna metóda,
Cvi enie z Teórie elektromagnetického po a 1. cvi enie ( ) Úvod Info o cvi iacom Meno: Luká² Tomek Katedra: Katedra teoretickej fyziky a didak
 Cvi eie z Teórie elektromagetického po a 1. cvi eie (13.2.212) Úvod Ifo o cvi iacom Meo: Luká² Tomek Katedra: Katedra teoretickej fyziky a didaktiky fyziky Oddeleie: Oddeleie didaktiky fyziky Miestos :
Cvi eie z Teórie elektromagetického po a 1. cvi eie (13.2.212) Úvod Ifo o cvi iacom Meo: Luká² Tomek Katedra: Katedra teoretickej fyziky a didaktiky fyziky Oddeleie: Oddeleie didaktiky fyziky Miestos :
Inflácia Nezamestnanosť
 Inflácia, deflácia, ekonomický cyklus Prednáška 10 Inflácia dlhodobý rast cenovej hladiny tovarov a služieb Zmena cien jednotlivých tovarov a služieb Zmena cenovej hladiny Zmena celkovej úrovne cien tovarov
Inflácia, deflácia, ekonomický cyklus Prednáška 10 Inflácia dlhodobý rast cenovej hladiny tovarov a služieb Zmena cien jednotlivých tovarov a služieb Zmena cenovej hladiny Zmena celkovej úrovne cien tovarov
10.priklady Lukasiewicz and Zadeh
 Cvični Cvični 9.. Zostrojt hrktristiké funki risp množín, ktoré rprzntujú intrvl rálnh čísl () (, ) I ( x) = ( x R) () 0, ) ( x 0, ) ) I ( x) 0 ( x (, 0 )) (), 0 (, 0) ( x, 0 (, 0) ) I ( x) 0 x, ) 0, 0,
Cvični Cvični 9.. Zostrojt hrktristiké funki risp množín, ktoré rprzntujú intrvl rálnh čísl () (, ) I ( x) = ( x R) () 0, ) ( x 0, ) ) I ( x) 0 ( x (, 0 )) (), 0 (, 0) ( x, 0 (, 0) ) I ( x) 0 x, ) 0, 0,
Návod na obsluhu Ultrazvukový reflexný spínač bez IO- Link SK UGT20x UGT21x UGT50x UGT52x / / 2019
 Návod na obsluhu Ultrazvukový reflexný spínač bez IO- ink UGTx UGTx UGT5x UGT5x 8775 / / 9 Bezpečnostné upozornenia Tento dokument si pred uvedením prístroja do prevádzky prečítajte a počas používania
Návod na obsluhu Ultrazvukový reflexný spínač bez IO- ink UGTx UGTx UGT5x UGT5x 8775 / / 9 Bezpečnostné upozornenia Tento dokument si pred uvedením prístroja do prevádzky prečítajte a počas používania
Čiastka 104/2004
 Strana 2558 Zbierka zákonov č. 252/2004 Čiastka 104 252 NA RIA DE NIE VLÁ DY Slo ven skej re pub li ky z 15. ap rí la 2004 o úhra de za vy ko na nie štát nych ve te ri nár nych čin nos tí súk rom ný mi
Strana 2558 Zbierka zákonov č. 252/2004 Čiastka 104 252 NA RIA DE NIE VLÁ DY Slo ven skej re pub li ky z 15. ap rí la 2004 o úhra de za vy ko na nie štát nych ve te ri nár nych čin nos tí súk rom ný mi
Milé študentky, milí študenti, v prvom rade vám ďakujeme za vyplnenie ankety. Táto anketa bola zameraná na zistenie vášho postoja ku kvalite výučby. J
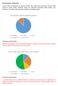 Milé študentky, milí študenti, v prvom rade vám ďakujeme za vyplnenie ankety. Táto anketa bola zameraná na zistenie vášho postoja ku kvalite výučby. Jednotlivé výroky sme vyhodnotili zastúpením vášho súhlasu,
Milé študentky, milí študenti, v prvom rade vám ďakujeme za vyplnenie ankety. Táto anketa bola zameraná na zistenie vášho postoja ku kvalite výučby. Jednotlivé výroky sme vyhodnotili zastúpením vášho súhlasu,
Pokyny_Doctorandorum dies
 (a) Forma príspevku Pokyny pre autorov/autorky článkov do konferenčného zborníku Príspevky možno písať v jazyku: slovenský, český, anglický, nemecký, francúzsky, ruský. Text, tabuľky, obrázky používať
(a) Forma príspevku Pokyny pre autorov/autorky článkov do konferenčného zborníku Príspevky možno písať v jazyku: slovenský, český, anglický, nemecký, francúzsky, ruský. Text, tabuľky, obrázky používať
Operačná analýza 2
 Niektoré náhodné procesy majú v praxi veľký význam, pretože sa často vyskytujú, napr.: Poissonov proces proces vzniku a zániku Wienerov proces stacionárne procesy,... Poissonov proces je homogénny Markovov
Niektoré náhodné procesy majú v praxi veľký význam, pretože sa často vyskytujú, napr.: Poissonov proces proces vzniku a zániku Wienerov proces stacionárne procesy,... Poissonov proces je homogénny Markovov
Zoznamové farbenia grafov
 Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Zoznamové farbenia grafov (Diplomová práca) Lukáš Špalek Vedúca: RNDr. Edita Máčajová, PhD. Bratislava, 2010
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Zoznamové farbenia grafov (Diplomová práca) Lukáš Špalek Vedúca: RNDr. Edita Máčajová, PhD. Bratislava, 2010
Snímka 1
 Bayesovský klasfkátor prradí objekt trede, kde P(ω x) je maxmálne Rozhodovaca funkca Ako určť pravdepodobnost Pre kategorcké atrbúty P( x ) P( ) P( x ) k d x k k1 N N, k Navný klasfkátor Pravdepodobnosť
Bayesovský klasfkátor prradí objekt trede, kde P(ω x) je maxmálne Rozhodovaca funkca Ako určť pravdepodobnost Pre kategorcké atrbúty P( x ) P( ) P( x ) k d x k k1 N N, k Navný klasfkátor Pravdepodobnosť
Rekurentné neurónové siete
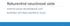 Reurentné neurónové sete HOPFIELDOA NEURÓNOÁ SIEŤ RIEŠENIE OPTIMALIZAČNÝCH ÚLOH Hopfeldova seť Hopfeldova seť so svoím učacm algortmom patrí do tredy plne reurentných setí s bnárnym vstupom, trénovaných
Reurentné neurónové sete HOPFIELDOA NEURÓNOÁ SIEŤ RIEŠENIE OPTIMALIZAČNÝCH ÚLOH Hopfeldova seť Hopfeldova seť so svoím učacm algortmom patrí do tredy plne reurentných setí s bnárnym vstupom, trénovaných
Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1
 Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1 A Pomocou Charpitovej metódy vyriešte rovnicu. x u x + y u y = u u x y u 2 = xy u u x y 3. u 2 y = u y u 4. u 2 x = u x u u x = B.
Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1 A Pomocou Charpitovej metódy vyriešte rovnicu. x u x + y u y = u u x y u 2 = xy u u x y 3. u 2 y = u y u 4. u 2 x = u x u u x = B.
III. WC sedadlá a úchyty MKW KÓD NÁZOV CENA/1 KS BALENIE KÓD ÚCHYTY KÓD MKW V EURO / KS NÁHRADNÉ DIELY WC SEDADLO UNIVERSAL ECO biele termoplas
 909118 UNIVERSAL ECO biele termoplast 9,99 1/10 ks Plast Trend - 909145/909160 S470V021 909115 UNIVERSAL biele termoplast 12,98 1 ks Plast Trend - 909145/909160 S470T010 909116 UNIVERSAL PLUS SC 15,90
909118 UNIVERSAL ECO biele termoplast 9,99 1/10 ks Plast Trend - 909145/909160 S470V021 909115 UNIVERSAL biele termoplast 12,98 1 ks Plast Trend - 909145/909160 S470T010 909116 UNIVERSAL PLUS SC 15,90
ZB_Daikin_SETUP_HPSU_compact_V52_ _00_0417_SK.book
 Kontrolný zoznam pre uvedenie do prevádzky V5.2 Daikin Altherma EHS(X/H)(B) - 04P30B - 08P30B - 08P50B - 16P50B Vykonané opatrenia označte! Slovenčina Vykonané opatrenia označte! Inicializácia: Vnútorný
Kontrolný zoznam pre uvedenie do prevádzky V5.2 Daikin Altherma EHS(X/H)(B) - 04P30B - 08P30B - 08P50B - 16P50B Vykonané opatrenia označte! Slovenčina Vykonané opatrenia označte! Inicializácia: Vnútorný
ZMLUVA O NÁRODNOM SPOLUFINANCOVANÍ ČÍSLO ZMLUVY:... TÁTO ZMLUVA je uzavretá medzi: 1. ZMLUVNÉ STRANY 1.1. Poskytovateľ názov: Ministerstvo pôdohospodá
 ZMLUVA O NÁRODNOM SPOLUFINANCOVANÍ ČÍSLO ZMLUVY:... TÁTO ZMLUVA je uzavretá medzi: 1. ZMLUVNÉ STRANY 1.1. Poskytovateľ názov: Ministerstvo pôdohospodárstva a rozvoja vidieka SR sídlo: Dobrovičova 12, 812
ZMLUVA O NÁRODNOM SPOLUFINANCOVANÍ ČÍSLO ZMLUVY:... TÁTO ZMLUVA je uzavretá medzi: 1. ZMLUVNÉ STRANY 1.1. Poskytovateľ názov: Ministerstvo pôdohospodárstva a rozvoja vidieka SR sídlo: Dobrovičova 12, 812
Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ LINEÁRNE A KVADRATICKÉ PROGRAMOVANIE Vysokoškolská učebnica F
 Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ LINEÁRNE A KVADRATICKÉ PROGRAMOVANIE Vysokoškolská učebnica Fakulta elektrotechniky a informatiky Štefan Berežný
Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ LINEÁRNE A KVADRATICKÉ PROGRAMOVANIE Vysokoškolská učebnica Fakulta elektrotechniky a informatiky Štefan Berežný
Analýza sociálnych sietí Geografická lokalizácia krajín EU
 Analýza sociálnych sietí Geografická lokalizácia krajín EU Ekonomická fakulta TU v Košiciach 20. februára 2009 Vzt ahy medzi krajinami - teória grafov Doterajšie riešenia 1 problém farbenia grafov (Francis
Analýza sociálnych sietí Geografická lokalizácia krajín EU Ekonomická fakulta TU v Košiciach 20. februára 2009 Vzt ahy medzi krajinami - teória grafov Doterajšie riešenia 1 problém farbenia grafov (Francis
Biharmonická rovnica - ciže co spôsobí pridanie jedného laplasiánu
 iºe o spôsobí pridanie jedného laplasiánu tyc struna Obsah ƒo je to biharmonická rovnica 2 Malý výlet do teórie pruºnosti 3 Rovnice, okrajové podmienky, rie²enia 4... a kde ostala matematická fyzika? ƒo
iºe o spôsobí pridanie jedného laplasiánu tyc struna Obsah ƒo je to biharmonická rovnica 2 Malý výlet do teórie pruºnosti 3 Rovnice, okrajové podmienky, rie²enia 4... a kde ostala matematická fyzika? ƒo
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú in
 Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Hlavon
 Problematika dopravy element uspokojovania potrieb obyvateľstva doc. Ing. Ivan Hlavoň, CSc. Vysoká škola logistiky o.p.s. 23. 11. 2017 Potreba premiestenia je rovnako stará ako ľudstvo Základné zloženie
Problematika dopravy element uspokojovania potrieb obyvateľstva doc. Ing. Ivan Hlavoň, CSc. Vysoká škola logistiky o.p.s. 23. 11. 2017 Potreba premiestenia je rovnako stará ako ľudstvo Základné zloženie
BRKOS
 Pomocný text Výroková logika autor: Viki Logika je nástroj, ktorý nám umoº uje matematicky uvaºova o veciach okolo nás. Dovo uje nám formalizova tvrdenia, ktoré chceme dokáza a zárove formalizova samotný
Pomocný text Výroková logika autor: Viki Logika je nástroj, ktorý nám umoº uje matematicky uvaºova o veciach okolo nás. Dovo uje nám formalizova tvrdenia, ktoré chceme dokáza a zárove formalizova samotný
Kolmogorovská zložitost
 Kolmogorovská zložitosť 5.12.2013 (2013/14) KZ 5.12.2013 1 / 16 Kt zložitosť age(x) = min p{2 l(p) t : U(p) = x v priebehu t krokov} Def. (Kt zložitosť) UTS monotonne skenuje začiatok p kým vypíše x, t(p,
Kolmogorovská zložitosť 5.12.2013 (2013/14) KZ 5.12.2013 1 / 16 Kt zložitosť age(x) = min p{2 l(p) t : U(p) = x v priebehu t krokov} Def. (Kt zložitosť) UTS monotonne skenuje začiatok p kým vypíše x, t(p,
PowerPoint Presentation
 Vymenujte základné body fyzikálneho programu ktoré určujú metodológiu fyziky pri štúdiu nejakého fyzikálneho systému Ako vyzerá pohybová rovnica pre predpovedanie budúcnosti častice v mechanike popíšte,
Vymenujte základné body fyzikálneho programu ktoré určujú metodológiu fyziky pri štúdiu nejakého fyzikálneho systému Ako vyzerá pohybová rovnica pre predpovedanie budúcnosti častice v mechanike popíšte,
bakalarska prezentacia.key
 Inteligentné vyhľadávanie v systéme na evidenciu skautských družinových hier Richard Dvorský Základné pojmy Generátor družinoviek Inteligentné vyhľadávanie Ako to funguje Základné pojmy Skautská družina
Inteligentné vyhľadávanie v systéme na evidenciu skautských družinových hier Richard Dvorský Základné pojmy Generátor družinoviek Inteligentné vyhľadávanie Ako to funguje Základné pojmy Skautská družina
Susedov rozli²ujúci index grafu Bakalárska práca pre ²tudijný program Matematika alebo Ekonomická a nan ná matematika v akademickom roku 2019/20 vedúc
 Bakalárska práca pre ²tudijný program Matematika alebo Ekonomická a nan ná matematika v akademickom roku 2019/20 vedúci práce pokra ovanie v diplomovej práci vítané G graf, C mnoºina farieb, ϕ : E(G) C
Bakalárska práca pre ²tudijný program Matematika alebo Ekonomická a nan ná matematika v akademickom roku 2019/20 vedúci práce pokra ovanie v diplomovej práci vítané G graf, C mnoºina farieb, ϕ : E(G) C
Čiastka 205/2004
 Strana 4282 Zbierka zákonov č. 481/2004 Čiastka 205 481 o zvý še ní sumy za o pat ro va cie ho prí spev ku Vlá da pod a 4 ods. 4 zá ko na č. 236/1998 Z. z. o za o pat ro va com prí spev ku v zne ní zá
Strana 4282 Zbierka zákonov č. 481/2004 Čiastka 205 481 o zvý še ní sumy za o pat ro va cie ho prí spev ku Vlá da pod a 4 ods. 4 zá ko na č. 236/1998 Z. z. o za o pat ro va com prí spev ku v zne ní zá
Snímka 1
 Fyzika - prednáška 12 Ciele 5. Fyzikálne polia 5.4 Stacionárne magnetické pole 5.5 Elektromagnetické pole Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Fyzika - prednáška 12 Ciele 5. Fyzikálne polia 5.4 Stacionárne magnetické pole 5.5 Elektromagnetické pole Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy
 Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy) alebo analyticky (výpočet súradníc bodov elipsy).
Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy) alebo analyticky (výpočet súradníc bodov elipsy).
TESTOVANIE STABILITY PROCESU POKRAČOVANIA GRADIOMETRICKÝCH MERANÍ DRUŽICE GOCE NADOL
 S L O V E N S K Á E C H N I C K Á U N I V E R Z I A V B R A I S L A V E S A V E B N Á F A K U L A K A E D R A G E O D E I C K Ý C H Z Á K L A D O V ESOVANIE SABILIY PROCESU POKRAČOVANIA GRADIOMERICKÝCH
S L O V E N S K Á E C H N I C K Á U N I V E R Z I A V B R A I S L A V E S A V E B N Á F A K U L A K A E D R A G E O D E I C K Ý C H Z Á K L A D O V ESOVANIE SABILIY PROCESU POKRAČOVANIA GRADIOMERICKÝCH
Microsoft Word - mikles_holik.doc
 TRIESKOVÉ A BEZTRIESKOVÉ OBRÁBANIE DREVA 006. - 4. 0. 006 95 ŠTÚDIUM GEOMETRIE NOŽOV A KINEMATIKY ODVETVOVACEJ HLAVICE LESNÉHO STROJA Mila Mikleš - Já Holík Abstract Is is usually techical roblem to fid
TRIESKOVÉ A BEZTRIESKOVÉ OBRÁBANIE DREVA 006. - 4. 0. 006 95 ŠTÚDIUM GEOMETRIE NOŽOV A KINEMATIKY ODVETVOVACEJ HLAVICE LESNÉHO STROJA Mila Mikleš - Já Holík Abstract Is is usually techical roblem to fid
