Microsoft Word - Duchon 2
|
|
|
- Lumír Fiala
- pred 4 rokmi
- Prehliadani:
Prepis
1 Globálna navgáca moblných robotov na báze geometrcke mapy Frantšek Duchoň Ladslav Juršca Abstrakt Článok analyzue súčasný stav problematky navgáce moblných robotov na základe známe geometrcke rezentáce prostreda. V článku sú predstavené základné metódy plánovana cesty robota v známom prostredí a zároveň sú analyzované ch výhody a nedostatky. Kľúčové slová: geometrcká mapa graf vdteľnost Voronoov dagram tangent graf polygónové mapy metóda napnutého vlákna metóda potencálových polí Úvod Naprek exstuúcm vhodneším rezentácám prostreda pre moblné roboty z hľadska ukladaceho prestoru a štruktúry zápsu sa v moblne robotke uplatňuú a geometrcké rezntáce prostreda obvykle tvorené polygónm. Naprek náročnost uchovávať takúto rezentácu prostreda sa v moblne robotke uplatňuú z rôznych hľadísk optmálne metódy hľadana nakratších cest v takýchto mapách [][7]. Medz takéto metódy možno zaradť graf vdteľnost všeobecný Voronoov dagram tangent graf metódu napnutého vlákna alebo metódu potencálových polí.. Graf vdteľnost [] [] Spoením všetkých párov vrcholov prekážok v prostredí (resp. v mape prostreda) ktoré sa navzáom "vda" vznkne graf na ktorom sa dá plánovať globálna dráha. Graf obsahue a počatočnú a ceľovú pozícu robota. Čary spáaúce ednotlvé vrcholy prekážok obvykle rezentuú nakratšu cestu medz týmto vrcholm. Úlohou robota e potom už len násť nakratšu cestu medz počatočnou a ceľovou pozícou v takto defnovanom grafe. Na to možno využť algortmy A* Dkstra (vď AT&P Journal Globálna navgáca moblných robotov na báze topologcke mapy) alebo ednoduché prehľadávane na základe eukldovske vzdalenost. Hrany grafu vdteľnost e sú rovné čary ktoré spáaú dva "vdteľné" vrcholy v a v : e s. v S s 0 0 s. v free () kde S free predstavue voľný prestor v prostredí. Nech množna V v... v n e množna vrcholov prekážok v konfguračnom prestore zahŕňaúca a štartovný a ceľový bod robota. Zostroene grafu vdteľnost spočíva v určení všetkých ostatných vdteľných vrcholov prekážok pre vrchol v V. Logcky sa ponúka možnosť otestovať všetky dvoce vrcholov č nepretínaú prekážky. Je teda potrebné otestovať O n prenkov pretože exstue n prekážok. Takže e tu O hrán od O n možných hrán z vrcholu v preto e potrebné otestovať n O vrcholov vdteľných pre vrchol v. To e nutné vykonať pre všetky v V čže výpo-. xstue však a čtová náročnosť sa zvýš až na O n efektívneša metóda ako určť vdteľné vrcholy pre vrchol v. Táto metóda sa nazýva plane sweep algortmus. Vstupom v a vrchol v. v vdteľná z vrcholu v. do tohto algortmu e množna vrcholov Výstupom e podmnožna z Algortmus spočíva v týchto krokoch:. Pre každý vrchol v sa vypočíta uhol medz horzontálnou osou (obvykle os x ) a čarou.. Vytvorí sa zoznam vrcholov obsahuúc vo vzostupnom poradí.. Vytvorí sa aktívny zoznam S obsahuúc hrany ktoré pretínaú polpramku v kladnom smere os x vychádzaúce z v. 4. Všetky e potrebné otestovať. Ak e v potom čaru v vdteľné z v začatkom hrany ktorá ne e v S e potrebné prdať do grafu vdteľnost. Ak e potom e potrebné vložť túto hranu do množny S. Ak v koncom hrany v S potom e potrebné túto hranu e vymazať zo zoznamu S. Príklad takéhoto algortmu možno ukázať na obrázku (Obr. ). ISSN -X /0 Teóra
2 Vlož 8 Vlož Vymaž Vlož Obr. Príklad prostreda pre vytvorene grafu vdteľnost [] Fg. xample of envronment used for vsblty graph creaton Naskôr sú vypočítané uhly k ednotlvým vrcholom a ncalzované množny S 4 8 a. Ďalší postup znázorňue tabuľka (Tab. ). Treba s uvedomť defnovane začatku a konca hrany. Začatok hrany e defnovaný menším uhlom od horzontálne os vytvorene z vrcholu v naopak konec hrany má väčší uhol od teto horzontálne os oprot začatku hrany. Vdteľnosť vrcholu v z v sa testue len vzhľadom na množnu S. Takýmto spôsobom sa výpočtová náročnosť algortmu znžue na On. log n. Ak sú náhodou tr vrcholy kolneárne (leža na edne pramke) eden vrchol sa merne posune a pokračue sa vyšše opísaným algortmom. 4 8 Tab. Postup výpočtu pomocou plane sweep algortmu [] Fg. Progress of computaton wth plane sweep algorthm Naprek ednoduche mplementác má táto metóda dva hlavné nedostatky. Veľkosť rezentáce prostreda a teda a počet vrcholov a cest v grafe sa zvyšue s množstvom prekážok v prostredí. Metóda e teda rýchla a efektívna v prostredí s menším počtom prekážok avšak pr väčšom počte prekážok e v porovnaní s ným metódam pomalá a neefektívna. Druhou nevýhodou e že nádená dráha v grafe vdteľnost predpsue robotu čo navac sa prblížť k prekážkam. Naprek tomu že nádená dráha e optmálna podmenky pre bezpečnosť robota ako a eho prostreda optmálne nastavené ne sú. Obvyklým rešením e defnovane rozšírena prekážok o vzdalenosť väčšu ako e polomer robota čo má však často za následok obetovane optmálnost nádene dráhy. Vymaž Vlož Vrchol Množna S Akca Incalzáca 4 8 Zoradene množny Vymaž Vlož Vymaž Vlož 7 Vymaž Vymaž 4 Prda 4 do grafu Vymaž 7 Vymaž 8 Prda 8 do grafu Vlož 4 Vlož Prda do grafu Obr. Graf vdteľnost [] Fg. Vsblty graph Z prve nevýhody vyplýva že graf vdteľnost (Obr. ) obsahue mnoho nadbytočných vrcholov. Použtím podporných a oddeľuúcch čar možno tento počet zredukovať (Obr. ). Podporná čara e dotyčnca k dvom prekážkam prčom obe prekážky sa nachádzaú len v edne pol rovne vymedzene čarou. Oddeľuúca čara e tak sto dotyčnca k dvom prekážkam avšak prekážky sa nachádzaú v opačných pol rovnách vymedzených čarou. Redukovaný graf (Obr. 4) vdteľnost e zostroený z práve takýchto podporných a oddeľuúcch čar. Uzly grafu vdteľnost ktoré neleža na takýchto čarach sú odstránené. Redukovaný graf vdteľnost možno zostroť a pre konkávne typy prekážok. Uplatňue sa tu defníca lokálne konvexnost. ISSN -X /0 Teóra
3 cesty Voronoovým dagramom môžeme prekážky pokladať za základne. Prekážky ne sú však opísane množnou bodov preto defnícu Voronoovho regónu e potrebné rozšírť na defnícu všeobecného Voronovho dagramu. Nech V e množna bodov nablžších k prekážke Q : V kde d q Q free d q d h q h () d q e vzdalenosť k prekážke Q z polohy q teda: q mn dq c () co Základným stavebným kameňom všeobecného Voronovho dagramu (VVD v angl. GVD - Generalsed Vorono Dagram) e množna ekvdštančných bodov ku dvom množnám Q a Q pre ktoré platí: d q d q 0 (4) Obr. Príklady podporných a oddeľuúcch čar [] Fg. xamples of supportng and segregatng lnes Dvoekvdštančná plocha e potom defnovaná ako (Obr. a): S q Q q q d d 0 () Takáto plocha rozdeľue prekážky v prestore a môžeme u obmedzť na množnu bodov ekvdštančných k prekážkam Q a Q ktoré sú zároveň nablžše k obom týmto prekážkam. Takáto obmedzená štruktúra sa nazýva dvoekvdštančný zlom (Obr. c): V q Q d q d q h () Spoením dvoch takýchto dvoekvdštančných zlomov vznkne VVD (Obr. d): VVD V (7) Obr. 4 Graf vdteľnost a redukovaný graf vdteľnost [] Fg. 4 Vsblty graph and reduced vsblty graph. Voronoov dagram [] [] [] [4] Voronoov dagram e cestná mapa ktorá maxmalzue vzdalenosť medz robotom a prekážkam v mape. Plánovane dráhy moblného robota pomocou Voronovho dagramu vychádza z geometrcke mapy prostreda. Pre každý bod patrac do množny voľných bodov (teda ne prekážky) e vypočítaná vzdalenosť k nablžše prekážke. Voronoov dagram e defnovaný na množnách bodov nazývaných základne. Voronoov regón e potom množna bodov nablžších k dane základn. Voronoov dagram e množna bodov ekvdštančných k dvom základnam. Pr plánovaní Obr. a.) Množna S ekvdštančných bodov k dvom prekážkam b.) Množna SS ekvdštančných bodov s ednoznačným gradentom c.) Množna V ekvdštančných bodov k dvom prekážkam d.) Voronoov dagram [] ISSN -X /0 Teóra
4 Fg. a.) Set S of equdstant ponts to both obstacles b.) Set SS of equdstant ponts wth unvocal gradent c.) Set V of equdstant ponts to both obstacles d.) Vorono dagram V dvorozmernom prestore potom V nazývame hrany VVD ktoré sa konča alebo na dotykových bodoch (množna ekvdštančných bodov k trom alebo vacerým prekážkam) alebo na hrančných bodoch (množna bodov ktorých vzdalenosť k prekážke e nulová). Používane funkce vzdalenost d (ednoznačné určene vzdalenost) predpokladá výskyt len konvexných prekážok v prestore čo e v mnohých prípadoch nereálne. Je teda potrebné konkávne prekážky rozdelť na vacero konvexných. Na Obr. možno vdeť rozdelene konkávne prekážky na dve konvexné dvoma rôznym spôsobm. Oba sú správne avšak každá z dekompozíc vytvára odlšné množny ekvdštančných bodov S k prekážkam O a O. Obr. Konkávna prekážka a e možnost rozdelena [] Fg. Concave obstacle and ther possbltes of partton Obr. 7 Umestnene robota v troch bodoch. V bode q a q neexstue lokálne mnmum. [] Fg. 7 Placement of robot n three postons. In poston q and q doesn't exst local mnmum. Pre gradenty platí: d d d q d q q d q q d q Je teda potrebné elmnovať časť dvoekvdštančne plochy s neednoznačným vektorom gradentu (Obr. 7). To e možné urobť zadefnovaním dvoekvdštančne surektívne plochy (Obr. b): (8) SS q q q Q d d (9) Voronoov dagram možno zostroť na základe troch typov rezentácí prostreda: na základe nformácí zo snímačov na základe polygónove mapy prostreda a na základe mrežkove (metrcke) rezentáce prostreda. VVD môže byť skonštruovaný pramo z nformácí zo snímačov. Používaúc senzory vzdalenost e možné robot navesť na dotykový alebo hrančný bod. Robot sa dostane na štruktúru VVD tak že sa pohybue smerom od nablžše prekážky dovtedy kým ne e v rovnake vzdalenost od dvoch prekážok. Túto charakterstku možno využť a pr reaktívne navgác (Obr. 8). Obr. 8Spôsob nádena štruktúry VVD pr reaktívne navgác [] Fg. 8 The way of Vorono dagram constructon at reactve navgaton Ak robot narazí na nový ešte nepreskúmaný dotykový bod zapamätá s z akého smeru na tento dotykový bod narazl. Potom dentfkue všetky nové hrany VVD vychádzaúce z tohto dotykového bodu. Z dotykového bodu potom robot skúma hranu VVD kým nenarazí na ďalší dotykový alebo hrančný bod. Ak robot narazí na ďalší dotykový bod celý proces sa rekurzívne opakue. Ak robot narazí na už preskúmaný dotykový bod robot dokončl cyklus vo VVD grafe a pokračue s ešte nepreskúmaným dotykovým bodom. Ak robot narazí na hrančný bod ednoducho sa otočí a vrát sa k dotykovému bodu s nepreskúmaným hranam VVD. V prípade že všetky hrany sú už preskúmané tvorba VVD e ukončená. Ak sa robot dostane na VVD e potrebné aby "stopoval" VVD teda aby platlo d q d q. Dotyčnca e potom defnovaná ako d q d q 0. To sa zhodue s prechodom čarou spáaúcou dotykové body nablžších prekážok a generovaním vektora pohybu kolmého na túto čaru (Obr. 9) Dotykové body VVD sú potom detegované na základe náhlych zmen nformácí o vzdalenost k edne z nablžších prekážok. Takýmto sledovaním VVD možno spresnť a odometrckú nformácu o polohe robota. Obr. 9 Smer pohybu po VVD. Smer e vždy kolmý na čaru ktorá spáa dva nablžše body dvoch nablžších prekážok [] Fg. 9 Drecton of robot on GVD. Drecton s always orthogonal on lne whch connects the two nearest ponts of the nearest obstacles. Vytvorene VVD na polygónove mape e ednoduché (Obr. 0). Táto mapa defnue prekážky pomocou vrcholov a hrán. Množna ekvdštančných bodov k dvom hranám e čara. Množna ekvdštančných bodov k dvom vrcholom e čara. Množna ekvdštančných bodov medz vrcholom a hranou e ISSN -X /0 Teóra
5 parabola. Prestor polygónove mapy e teda potrebné rozdelť na čast s odpovedaúcm dvocam. Obr. 0 VVD medz dvoma polygónovým prekážkam [] Fg. 0 GVD between two polygonal obstacles. Na určene VVD v mrežkove rezentác sa používa Brushfre algortmus (vď. AT&P Journal Globálna navgáca moblných robotov na báze metrcke mapy). Pr teto metóde má každá bunka defnovanú vzdalenosť akú "vlna už prešla". Práve v bunkách kde sa vlna "láme" sú rovnaké vzdalenost k dvom nablžším prekážkam. Teto mesta sú potom súčasťou VVD. Lom vlny môžeme defnovať ako mesta s aktuálne šírenou hodnotou nedotýkaúce sa žadne bunky s nulovou hodnotou. Iným spôsobom detegovana bunek VVD e pamätane s od ktore prekážky sa vlna v dane bunke šír. Ak sa algortmus pokús zapísať pre ednu bunku dve rôzne hodnoty potom táto bunka e súčasťou VVD. Algortmy ktoré prehľadávaú cestu vo Voronoovom dagrame sú podobné ako pr metóde graf vdteľnost. Nádená dráha vo Voronoovom dagrame ne e optmálna z hľadska predene dĺžky e však nabezpečneša z hľadska kolízí. Obmedzením pre využte Voronovho dagramu e a druh použtých snímačov na lokalzácu robota v prostredí. Keďže táto metóda predpsue naväčšu vzdalenosť robota od prekážok akékoľvek senzory s krátkym dosahom použté pre lokalzácu môžu v tomto procese zlyhávať. Obr. Voronoov dagram [] Fg. Vorono dagram. Tangent graf [] Táto metóda bola vyvnutá kvôl nedostatkom grafu vdteľnost: Graf vdteľnost potrebue N predstavue počet vrcholov. O pamäte kde N Graf vdteľnost e obmedzený na prekážky polygonálneho tvaru zataľ čo v skutočnost prekážky mávaú rôzne zakrvena. Ak sa zmení neaký parameter pr výpočte grafu vdteľnost (napríklad počet prekážok alebo zmena rozmeru robota) e potrebné celý graf určť nanovo. Na rešene týchto nedostatkov bol zadefnovaný tangent graf. Pr určovaní tangent grafu bol zavedený poem lokálne nakratša cesta ktorý bol zavedený kvôl hľadanu cesty medz zakrveným hranam prekážok. Táto cesta predstavue nakratšu cestu na zvolenom malom regóne. Tangent graf sa podobá grafu vdteľnost avšak vrcholy tohto grafu zodpovedaú dotykovým bodom s prekážkam v zmysle lokálnych nakratších cest a eho hrany rezentuú pre pohyb robota voľné dotyčnce alebo konvexné dotykové segmenty medz vrcholm. Pomocou tangent grafu e možné hľadať cestu nelen medz prekážkam rezentovaným polygónm ale a medz prekážkam ktoré maú zakrvené hrany. Výpočtová náročnosť tangent grafu e O K kde K predstavue počet konvexných segmentov na hrancach prekážok. Cesta P e lokálne nakratša cesta ak na malom okolí ne e možné násť kratšu bezkolíznu cestu ako P. Je teda možné konštatovať že ak neexstue žadna lokálne nakratša cesta v mape potom neexstue bezkolízna cesta pre pohyb robota a naopak. Ak sa čara dotýka hrance prekážky v bode p ale nepretína žaden malý regón z prekážky v blízkost bodu p potom táto čara e dotyčnca k prekážke a bod p e nazývaný dotykový bod. Navyše ak e táto čara dotyčncou naraz k dvom prekážkam nazýva sa všeobecná dotyčnca. Ak sa dotykové body dotyčnce k obom alebo vacerým prekážkam nachádzaú na edne strane dotyčnce de o vonkašu všeobecnú dotyčncu nak o vnútornú všeobecnú dotyčncu. Ak sponca dvoch bodov z hrance prekážky defnovaných na malom poztívnom okolí bodu p z hrance prekážky e vo vnútr prekážky potom bod p e konvexný nak e konkávny. Ak sú všetky body zo segmentu hrance prekážky C konvexné potom a segment C e konvexný. Ak sú všetky body tohto segmentu konkávne potom a segment C e konkávny. Pre robot e potom lokálne nakratša cesta zostavená z konvexných hrančných segmentov a zo všeobecných dotyčníc konvexných hrančných segmentov. Prvú časť tohto tvrdena možno ukázať na oblúku ~ F ~. Predpokladame že oblúk ~ F ~ (Obr. ) e súčasťou lokálne nakratše cesty. Na malom okolí oblúka ~ F ~ e možné násť bod G kde pramy segment G e bezkolízny. Platí že ~ ~ ~~ G GF F. Druhú časť tvrdena možno ukázať na segmentoch CD a B ~ C ~. Predpokladame že segment CD e súčasťou lokálne nakratše cesty prechádzaúc do segmentu B ~ C ~. Segment CD ne e dotyčncou v bode C ale môžeme povedať že e dotyčncou k ným hrančným segmentom. Nablžším dotykovým bodom k bodu C zo segmentu CD e bod P. Potom môžeme podobne na okolí bodu C násť bod H na hranc B ~ C ~ ~ ~ pre ktorý platí že segment HP e bezkolízny a HP HC CP. ISSN -X /0 Teóra
6 cestu pre robot zo štartovace do ceľove pozíce možno násť metódam ktoré prehľadávaú grafy napr. A* alebo Dkstra algortmus. Obr. Vzťahy medz lokálne nakratším cestam hrancam a segmentm spáaúcm body na hrancach [] Fg. Relatons between locally shortest paths borders and segments lnkng pont on borders Tangent graf e potom defnovaný ako množna V L kde vrchol v V rezentue dotykový bod na hranc prekážky a hrana l L odpovedá bezkolízne všeobecne dotyčnc alebo konvexnému hrančnému segmentu medz dvoma bodm dotyku. Počet dotyčníc potom určue veľkosť tangent grafu. Pre dva konvexné obekty exstuú dve vnútorné a dve vonkaše všeobecné dotyčnce. Dokázať to možno tak že čara rozdeľue rovnu na dve pol rovny (Obr. ). Ak e táto čara dotyčncou k obom regónom regóny sa musa nachádzať v opačných pol rovnách. Z toho vyplýva že pre dva konvexné obekty môžu exstovať len dve vnútorné a dve vonkaše všeobecné dotyčnce. Obr. Porovnane grafu vdteľnost (a) a tangent grafu (b) [] Fg. Comparson of vsblty graph (a) and tangent graph (b). 4. Polygónové mapy [] Táto metóda vytvára na základe geometrcke mapy prostreda polygónovú rezentácu tohto prostreda (Obr. ). Táto rezentáca prostreda transformue voľný prestor do konvexných polygónov. Obr. Dotyčnce medz dvoma konvexným obektm [] Fg. Tangents between two convex obstacles xstue nanavýš 9 bezkolíznych dotyčníc medz dvoma šprálam. xstuú tr typy bezkolíznych dotyčníc medz dvoma šprálam. Prvý typ nkdy nepretne šprály (Obr. 4 a). Druhý typ pretne hocktorú zo šprál len raz (Obr. 4 b). Tretí typ pretne obe šprály (Obr. 4 c d). Obr. 4 Dotyčnce medz dvoma šprálam [] Fg. 4 Tangets between two sprals Z tvrdení o maxmálnom počte dotyčníc medz dvoma konvexným obektm a dvoma šprálam možno odvodť veľkosť tangent grafu. Ak e prostrede defnované tangent grafom ISSN -X Obr. Rozdelene prestoru na konvexné polygóny [] Fg. Partton of envronment on convex polygons Samotné polygóny v týchto mapách maú ednu dôležtú vlastnosť. Ak robot štartue na obvode nektorého z polygónov a potrebue sa dostať na ný bod z obvodu tohto polygónu nkdy neprede za okra polygónu. Polygón teda rezentue bezpečné pásmo prechodu pre robot. Plánovane dráhy na základe taketo mapy e potom otázkou výberu správneho porada polygónov ktorým treba presť. Konštrukca taketo mapy e položená na základe globálne geometrcke mapy. Naskôr sú prekážky "obalené" veľkosťou robota. Je to namä z bezpečnostného dôvodu. Druhým aspektom e možnosť rezentovať robot bodom. Ďale e potrebné v globálne metrcke mape násť význačné vlastnost prostreda z hľadska navgáce napr. rohy dvere hrance obektov apod. Na základe týchto vlastností e možné potom vygenerovať samotné polygóny. A keď sa môže zdať že plánovane na taketo mape e už ednoduché ne e celkom tomu tak. Nektoré čary tvorace hrance polygónu nemusa byť napoené na ďalší polygón (napríklad ak sú súčasťou prekážky) takže pre plánovane ch ne e možné brať do úvahy. Iné čary môžu byť prílš dlhé čo spôsobue rôzne celkové dráhy pr plánovaní. Keďže e ťažké dskretzovať čarové segmenty ponúka sa vacero rešení. Jedným /0 Teóra
7 z nch e násť stredné body čar polygónov (Obr. 7) ktoré suseda s ďalším polygónom. Tak vznkne graf na ktorom e pomocou grafových metód (Dsktra A* apod.) možné naplánovať dráhu. Obr. 7 Nádene cesty pomocou stredných bodov čar [] Fg. 7 Path searchng wth mddle ponts of lnes Ako e vdeť plánovane dráhy na takto vytvorene mape bude vždy neakým spôsobom bez hladkého prebehu dráhy. Z tohto dôvodu Chuck Thorpe navrhol rešene nazývané metóda napnutého vlákna (Obr. 8). Navrhnutá dráha robota e vytvorená akoby napnutým vláknom ktoré spáa oba konce prechodu polygónom. Takto navrhnutý algortmus vyhladí prebeh dráhy bez narušena bezpečnost prechodu polygónm. Obr. 8 Nádene cesty pomocou napnutého vlákna [] Fg. 8 Path searchng wth tghtenng rope Nevýhodam použta polygónových máp e veľká výpočtová náročnosť samotné využte vlastností prostreda z globálne mapy namesto využta snímaných údaov a otázka aktualzáce taketo mapy.. Metóda potencálových polí [] [4] Táto metóda vytvára pole alebo gradent na globálne geometrcke mape prostreda. Metóda potencálového poľa považue robot za bod ktorý e ovplyvnený umelým potencálovým polom U p. Robot sa v prostredí pohybue pomocou sledovana tohto poľa. Ceľ e defnovaný ako mnmum v prestore a správa sa ako príťažlvá sla zataľ čo prekážky maú predpísané správane v podobe odpudvých síl. Superpozícou všetkých síl aplkovaných na robot vznkne umelé potencálové pole ktoré plynule dovede robot do ceľove pozíce bez kontaktu s prekážkam. Predpokladame že robot e v dvorozmernom prestore defnovaný ako bod s orentácou teda pomocou x y. U p Ak zavedeme dferencálovú potencálovú funkcu môžme potom zadefnovať a umelú slu F p pôsobacu p x y : na pozíc Fp U p kde U p (0) označue gradent vektora U na pozíc p : p U U U x y U () Potencálové pole pôsobace na robot e potom vypočítané ako suma príťažlvého poľa od ceľa a odpudzuúcch polí od prekážok: U p U p U p () Podobne môžeme defnovať a sly pôsobace na robot: F p F p F p U p U p () Ďalším krokom v defnovaní umelého potencálového poľa e defníca príťažlvého a odpudvého potencálu. Príťažlvý potencál môže byť defnovaný napríklad takto: U kde p k p (4) k e kladný súčnteľ a súčnteľ p e defnovaný ako ukldovská vzdalenosť možno defnovať a príťažlvú slu F k F : p p p U p k p p p p. Podobne () Táto sla konvergue k 0 ak sa robot blíž k ceľu. Hlavnou myšlenkou defníce odpudvého potencálu e vygenerovať odpudvé sly od všetkých známych prekážok. Tento potencál resp. sla by mal byť veľm veľký v blízkost prekážok nemal by však ovplyvňovať pohyb robota vo veľke vzdalenost od týchto prekážok. Príkladom takéhoto odpudvého potencálu môže byť: U kde req k ρ p 0 p p 0 0 ρ k e opäť súčnteľ p p 0 () e mnmálna kolmá vzdalenosť od pozíce robota k obektu a 0 e vzdalenosť vplyvu obektu na dráhu robota. Obdobne e možné defnovať a odpudvú slu F : ISSN -X /0 Teóra
8 F req k p ρ U p ρ p p p p p - p prek p 0 (7) kde p e pozíca prekážky ktorá vplýva na dráhu robota. prek Výslednú slu môžeme defnovať ako súčet príťažlve a odpudvých síl. Pr deálnych podmenkach možno nastavť vektor rýchlost robota proporčne vzhľadom na vektor výsledne sly a robot by mal hladko smerovať do ceľa. Avšak tento prístup e obmedzený vzhľadom na exstencu lokálnych mním vyplývaúcch z tvaru a veľkost prekážok. Ďalší problém sa obavue pr výskyte konkávnych prekážok. Pr taketo prekážke sa obaví nekoľko mnmálnych vzdaleností p čo vede na osclácu robota medz dvoma nablžším bodm k obektu. Lteratúra [] CHOST H. LYNCH K. M. HUTCHINSON S. KANTOR G. BURGARD W. KAVRAKI L.. THRUN S.: Prncples of Robot Moton (Theory Algorthms and Implementatons). Massachusetts Insttute of Technology 00. ISN [] SIGWART R. NOURBAKHSH I.R.: Introducton to Autonomous Moble Robots. Massachusetts Insttute of Technology 004. ISBN [] MURPHY R. R.: Introducton to AI Robotcs. Massachusetts Insttute of Technology 000. ISBN [4] NIMULLR T. WIDYADHARMA S.: Artfcal Intellgence - An Introducton to Robotcs. In: prosemnar Artfcal Intellgence 00. [] LIU Y.-H. ARIMOTO S.: Proposal of Tangent Graph and xtended Tangent Graph for Path Plannng of Moble Robots. Proceedngs of the 99 I Intematonal Conference on Robotcs and Automaton Sacramento Calfoma Aprl 99 p. -7. [] HARGAŠ L. HRIANKA M. KONIAR D.: Image Processng and Analyss. A Practcal Approach Text Book (CD-ROM) Žlnská unverzta v Žlne 008 ISBN [7] SMRČK J. BOBOVSKÝ Z. FRIGA P.: Inovačné prístupy rešena. Stroárstvo Roč. č. (009) s. -. Abstract The paper analyss current state of moble robots navgaton on bass of known geometrcal resentaton of envronment. In paper are presented basc methods of path plannng n known envronment and there are presented advantages and dsadvantages of mentoned methods. Obr. 9 Prechod robota prostredím pomocou metódy umelého potencálového poľa s vykreslením ekvpotencálových čar [] Fg. 9 Path of robot n envronment callculated by artfcal potental feld and wth portrayal of equpotentonal lnes Poďakovane Tento článok vznkol pr rešení proektu VMSP-P prof. Ing. Ladslav Juršca PhD. Ing. Frantšek Duchoň PhD. Fakulta elektrotechnky a nformatky Ústav radena a premyselne nformatky Ilkovčova 8 9 Bratslava ladslav.ursca@stuba.sk frantsek.duchon@stuba.sk ISSN -X /0 Teóra
APROXIMÁCIA BINOMICKÉHO ROZDELENIA NORMÁLNYM A PRÍKLAD JEJ APLIKÁCIE V AKTUÁRSTVE S VYUŽITÍM JAZYKA R Abstrakt Príspevok sa zameriava na prezentáciu l
 APROXIMÁCIA BINOMICKÉHO ROZDELENIA NORMÁLNYM A PRÍKLAD JEJ APLIKÁCIE V AKTUÁRSTVE S VYUŽITÍM JAZYKA R Abstrakt Príspevok sa zamerava na prezentácu lmtných vet v analýze rzka v nežvotnom postení. Jednoducho
APROXIMÁCIA BINOMICKÉHO ROZDELENIA NORMÁLNYM A PRÍKLAD JEJ APLIKÁCIE V AKTUÁRSTVE S VYUŽITÍM JAZYKA R Abstrakt Príspevok sa zamerava na prezentácu lmtných vet v analýze rzka v nežvotnom postení. Jednoducho
Priebeh funkcie
 Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
Snímka 1
 Bayesovský klasfkátor prradí objekt trede, kde P(ω x) je maxmálne Rozhodovaca funkca Ako určť pravdepodobnost Pre kategorcké atrbúty P( x ) P( ) P( x ) k d x k k1 N N, k Navný klasfkátor Pravdepodobnosť
Bayesovský klasfkátor prradí objekt trede, kde P(ω x) je maxmálne Rozhodovaca funkca Ako určť pravdepodobnost Pre kategorcké atrbúty P( x ) P( ) P( x ) k d x k k1 N N, k Navný klasfkátor Pravdepodobnosť
Operačná analýza 2
 Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy
 Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy) alebo analyticky (výpočet súradníc bodov elipsy).
Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy) alebo analyticky (výpočet súradníc bodov elipsy).
Hladanie motívov v DNA sekvenciách
 Slovenská techncká unverzta v Bratslave Fakulta nformatky a nformačných technológí FIIT-5208-49439 Bc. Róbert Cuprk Hl adane motívov v DNA sekvencách Dplomová práca Vedúc práce: prof. Ing. Pavol Návrat,
Slovenská techncká unverzta v Bratslave Fakulta nformatky a nformačných technológí FIIT-5208-49439 Bc. Róbert Cuprk Hl adane motívov v DNA sekvencách Dplomová práca Vedúc práce: prof. Ing. Pavol Návrat,
A 1
 Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) Matematická analýza IV (ÚMV/MAN2d/10) RNDr. Lenka Halčinová, PhD.
 III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
9.1 MOMENTY ZOTRVACNOSTI \(KVADRATICKÉ MOMENTY\) A DEVIACNÝ MOMENT PRIEREZU
 Učebný cieľ kapitoly Po preštudovaní tejto kapitoly by ste mali ovládať: Charakteristiku kvadratických momentov prierezových plôch. Ako je definovaný kvadraticky moment plochy k osi a k pólu. Ako je definovaný
Učebný cieľ kapitoly Po preštudovaní tejto kapitoly by ste mali ovládať: Charakteristiku kvadratických momentov prierezových plôch. Ako je definovaný kvadraticky moment plochy k osi a k pólu. Ako je definovaný
Ďalšie vlastnosti goniometrických funkcií
 Ďalšie vlastnosti goniometrických funkcií Na obrázku máme bod B na jednotkovej kružnici, a rovnobežne s y-ovou osou bodom B vznikol pravouhlý trojuholník. Jeho prepona je polomer kružnice má veľkosť 1,
Ďalšie vlastnosti goniometrických funkcií Na obrázku máme bod B na jednotkovej kružnici, a rovnobežne s y-ovou osou bodom B vznikol pravouhlý trojuholník. Jeho prepona je polomer kružnice má veľkosť 1,
Matematický model činnosti sekvenčného obvodu 7 MATEMATICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčnéh
 7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
Snímka 1
 Fyzika - prednáška 11 Ciele 5. Fyzikálne polia 5.2 Elektrostatické pole 5.3 Jednosmerný elektrický prúd Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Fyzika - prednáška 11 Ciele 5. Fyzikálne polia 5.2 Elektrostatické pole 5.3 Jednosmerný elektrický prúd Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/ ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných r
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 009/010 59. ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných reálnych čísel, ktoré sú riešením sústavy rovníc a b c
SK MATEMATICKÁOLYMPIÁDA skmo.sk 009/010 59. ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných reálnych čísel, ktoré sú riešením sústavy rovníc a b c
Microsoft Word - skripta3b.doc
 6. Vlastnosti binárnych relácií V tejto časti sa budeme venovať šiestim vlastnostiam binárnych relácií. Najprv si uvedieme ich definíciu. Reláciu R definovanú v množine M nazývame: a ) reflexívnou, ak
6. Vlastnosti binárnych relácií V tejto časti sa budeme venovať šiestim vlastnostiam binárnych relácií. Najprv si uvedieme ich definíciu. Reláciu R definovanú v množine M nazývame: a ) reflexívnou, ak
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom
 2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
17. medzinárodná vedecká konferencia Riešenie krízových situácií v špecifickom prostredí, Fakulta špeciálneho inžinierstva ŽU, Žilina, máj 2
 17. medznárodná vedecká konferenca Rešene krízových stuácí v špecfckom prostredí, Fakulta špecálneho nžnerstva ŽU, Žlna, 30. - 31. máj 2012 PRÍSTUPY KU KVANTIFIKÁCII DOSLEDKOV DISFUNKCIE KRITICKEJ INFRAŠTRUKTÚRY
17. medznárodná vedecká konferenca Rešene krízových stuácí v špecfckom prostredí, Fakulta špecálneho nžnerstva ŽU, Žlna, 30. - 31. máj 2012 PRÍSTUPY KU KVANTIFIKÁCII DOSLEDKOV DISFUNKCIE KRITICKEJ INFRAŠTRUKTÚRY
Microsoft Word - FRI”U M 2005 forma B k¾úè.doc
 Fakulta riadenia a informatik Žilinskej univerzit ( ) ( 6 ) 6 = 3 () 8 (D) 8 m Závislosť hmotnosti m častice od jej rýchlosti v je vjadrená vzťahom m =, kde m je v c pokojová hmotnosť častice, c je rýchlosť
Fakulta riadenia a informatik Žilinskej univerzit ( ) ( 6 ) 6 = 3 () 8 (D) 8 m Závislosť hmotnosti m častice od jej rýchlosti v je vjadrená vzťahom m =, kde m je v c pokojová hmotnosť častice, c je rýchlosť
Operačná analýza 2
 Súradnicové sústavy a zobrazenia Súradnicové sústavy v rovine (E 2 ) 1. Karteziánska súradnicová sústava najpoužívanejšia súradnicová sústava; určená začiatkom O, kolmými osami x, y a rovnakými jednotkami
Súradnicové sústavy a zobrazenia Súradnicové sústavy v rovine (E 2 ) 1. Karteziánska súradnicová sústava najpoužívanejšia súradnicová sústava; určená začiatkom O, kolmými osami x, y a rovnakými jednotkami
Paralelné algoritmy, cast c. 3
 Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Naučme sa pripraviť a zrealizovať počítačom podporovaný experiment
 Laboratórne cvčena podporované počítačom epelné deje v plynoch Meno:...Škola:...reda:.... Izotermcký dej v deálnom plyne Fyzkálny prncíp: Pr pomalom stláčaní vzduchu pod pestom njekčnej strekačky zostáva
Laboratórne cvčena podporované počítačom epelné deje v plynoch Meno:...Škola:...reda:.... Izotermcký dej v deálnom plyne Fyzkálny prncíp: Pr pomalom stláčaní vzduchu pod pestom njekčnej strekačky zostáva
Klasická metóda CPM
 Operačná analýza 2-02a Klasická metóda CPM Úvod Je daná úloha časového plánovania U s množinou elementárnych činností E a reálnou funkciou c: E R ktorá každej činnosti A E priradí jej dobu trvania c(a).
Operačná analýza 2-02a Klasická metóda CPM Úvod Je daná úloha časového plánovania U s množinou elementárnych činností E a reálnou funkciou c: E R ktorá každej činnosti A E priradí jej dobu trvania c(a).
Microsoft Word - kriteria_ubyt_ doc
 Krtérá pre prdeľovane ubytovana študentom denného štúda na FIIT STU Čl. 1 Úvodné ustanovena (1) Krtérá pre prdeľovane ubytovana sa vypracovávajú za účelom zostavena poradovníka žadateľov o ubytovane v
Krtérá pre prdeľovane ubytovana študentom denného štúda na FIIT STU Čl. 1 Úvodné ustanovena (1) Krtérá pre prdeľovane ubytovana sa vypracovávajú za účelom zostavena poradovníka žadateľov o ubytovane v
trafo
 Výpočet rozptylovej reaktancie transformátora Vo väčších transformátoroch je X σk oveľa väčšia ako R k a preto si vyžaduje veľkú pozornosť. Ak magnetické napätia oboch vinutí sú presne rovnaké, t.j. N
Výpočet rozptylovej reaktancie transformátora Vo väčších transformátoroch je X σk oveľa väčšia ako R k a preto si vyžaduje veľkú pozornosť. Ak magnetické napätia oboch vinutí sú presne rovnaké, t.j. N
Pokrocilé spracovanie obrazu - Fourierová transformácia
 Pokročilé spracovanie obrazu - Fourierová transformácia Ing. Viktor Kocur viktor.kocur@fmph.uniba.sk DAI FMFI UK 29.11.2017 Obsah 1 Segmentácia O čo ide 2 Watershed Princíp Postup 3 k-means clustering
Pokročilé spracovanie obrazu - Fourierová transformácia Ing. Viktor Kocur viktor.kocur@fmph.uniba.sk DAI FMFI UK 29.11.2017 Obsah 1 Segmentácia O čo ide 2 Watershed Princíp Postup 3 k-means clustering
Microsoft Word - mpicv11.doc
 1. Vypočítajte obsah plochy ohraničenej súradnicovými osami a grafom funkcie y = x. a) vypočítame priesečníky grafu so súradnicovými osami x=... y = = y =... = x... x= priesečníku grafu funkcie so ; a
1. Vypočítajte obsah plochy ohraničenej súradnicovými osami a grafom funkcie y = x. a) vypočítame priesečníky grafu so súradnicovými osami x=... y = = y =... = x... x= priesečníku grafu funkcie so ; a
Informačná a modelová podpora pre kvantifikáciu prvkov daňovej sústavy SR
 Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
andrejkova-kazimir
 Rozpoznávane bometrckých údaov pomocou neurónových setí dentfkačné znaky ucha Gabrea Andreková Peter Kažmír Ústav nformatky Prírodovedecká fakuta UPJŠ Jesenná 5 Košce E-ma: Gabrea.Andrekova@ups.sk Peter.Kazmr@gma.com
Rozpoznávane bometrckých údaov pomocou neurónových setí dentfkačné znaky ucha Gabrea Andreková Peter Kažmír Ústav nformatky Prírodovedecká fakuta UPJŠ Jesenná 5 Košce E-ma: Gabrea.Andrekova@ups.sk Peter.Kazmr@gma.com
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú in
 Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Microsoft Word - mnohouholnik.doc
 Výpočet obsahu mnohouholníka Mnohouholník je daný súradnicami svojich vrcholov: A1[x1, y1], A2[x2, y2],..., An[xn, yn]. Aby sme sa vyhli komplikáciám, obmedzíme sa na prípad konvexného mnohouholníka. Súradnice
Výpočet obsahu mnohouholníka Mnohouholník je daný súradnicami svojich vrcholov: A1[x1, y1], A2[x2, y2],..., An[xn, yn]. Aby sme sa vyhli komplikáciám, obmedzíme sa na prípad konvexného mnohouholníka. Súradnice
Susedov rozli²ujúci index grafu Bakalárska práca pre ²tudijný program Matematika alebo Ekonomická a nan ná matematika v akademickom roku 2019/20 vedúc
 Bakalárska práca pre ²tudijný program Matematika alebo Ekonomická a nan ná matematika v akademickom roku 2019/20 vedúci práce pokra ovanie v diplomovej práci vítané G graf, C mnoºina farieb, ϕ : E(G) C
Bakalárska práca pre ²tudijný program Matematika alebo Ekonomická a nan ná matematika v akademickom roku 2019/20 vedúci práce pokra ovanie v diplomovej práci vítané G graf, C mnoºina farieb, ϕ : E(G) C
Statika (2.vydanie)
 ŽILINSKÁ UNIVERZITA V ŽILINE Fakulta špecálneho nžnerstva Doc. Ing. Jozef KOVAČIK, CSc. Ing. Martn BENIAČ, PhD. STATIKA PRE ŠPECIÁLNE INŽINIERSTVO Druhé doplnené a upravené vydane Určené pre študjné odbory
ŽILINSKÁ UNIVERZITA V ŽILINE Fakulta špecálneho nžnerstva Doc. Ing. Jozef KOVAČIK, CSc. Ing. Martn BENIAČ, PhD. STATIKA PRE ŠPECIÁLNE INŽINIERSTVO Druhé doplnené a upravené vydane Určené pre študjné odbory
Preco kocka stací? - o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, ked sú velké
 o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
Microsoft Word - Diskusia11.doc
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky MATEMATIKA - 011 sem vlepiť čiarový kód uchádzača Test obsahuje 30 úloh. Na jeho vypracovanie máte 90 minút. Každá úloha spolu
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky MATEMATIKA - 011 sem vlepiť čiarový kód uchádzača Test obsahuje 30 úloh. Na jeho vypracovanie máte 90 minút. Každá úloha spolu
1 Rekurencie este raz riesenia niektorych rekurencii z cvik. mame danu rekurenciu napr T (n) = at ( n b ) + k. idea postupu je postupne rozpisovat cle
 1 Rekurencie este raz riesenia niektorych rekurencii z cvik. mame danu rekurenciu napr at b + k. idea postupu je postupne rozpisovat cleny T b... teda T b = at + 1... dokym v tom neuvidime nejaky tvar
1 Rekurencie este raz riesenia niektorych rekurencii z cvik. mame danu rekurenciu napr at b + k. idea postupu je postupne rozpisovat cleny T b... teda T b = at + 1... dokym v tom neuvidime nejaky tvar
O možnosti riešenia deformácie zemského povrchu z pohladu metódy konecných prvkov konference pro studenty matematiky
 O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
Republika Srbsko MINISTERSTVO OSVETY, VEDY A TECHNOLOGICKÉHO ROZVOJA ÚSTAV PRE HODNOTENIE KVALITY VZDELÁVANIA A VÝCHOVY VOJVODINSKÝ PEDAGOGICKÝ ÚSTAV
 Republika Srbsko MINISTERSTVO OSVETY, VEDY A TECHNOLOGICKÉHO ROZVOJA ÚSTAV PRE HODNOTENIE KVALITY VZDELÁVANIA A VÝCHOVY VOJVODINSKÝ PEDAGOGICKÝ ÚSTAV ZÁVEREČNÁ SKÚŠKA NA KONCI ZÁKLADNÉHO VZDELÁVANIA A
Republika Srbsko MINISTERSTVO OSVETY, VEDY A TECHNOLOGICKÉHO ROZVOJA ÚSTAV PRE HODNOTENIE KVALITY VZDELÁVANIA A VÝCHOVY VOJVODINSKÝ PEDAGOGICKÝ ÚSTAV ZÁVEREČNÁ SKÚŠKA NA KONCI ZÁKLADNÉHO VZDELÁVANIA A
Slide 1
 SÚSTAVA TRANSF. VZŤAHY Plošné, objemové element Polárna Clindrická rcos rsin rcos r sin z z ds rddr dv rddrdz rcossin Sférická r sin sin dv r sin drd d z rcos Viacrozmerné integrál vo fzike Výpočet poloh
SÚSTAVA TRANSF. VZŤAHY Plošné, objemové element Polárna Clindrická rcos rsin rcos r sin z z ds rddr dv rddrdz rcossin Sférická r sin sin dv r sin drd d z rcos Viacrozmerné integrál vo fzike Výpočet poloh
Analýza sociálnych sietí Geografická lokalizácia krajín EU
 Analýza sociálnych sietí Geografická lokalizácia krajín EU Ekonomická fakulta TU v Košiciach 20. februára 2009 Vzt ahy medzi krajinami - teória grafov Doterajšie riešenia 1 problém farbenia grafov (Francis
Analýza sociálnych sietí Geografická lokalizácia krajín EU Ekonomická fakulta TU v Košiciach 20. februára 2009 Vzt ahy medzi krajinami - teória grafov Doterajšie riešenia 1 problém farbenia grafov (Francis
Snímka 1
 Fyzika - prednáška 12 Ciele 5. Fyzikálne polia 5.4 Stacionárne magnetické pole 5.5 Elektromagnetické pole Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Fyzika - prednáška 12 Ciele 5. Fyzikálne polia 5.4 Stacionárne magnetické pole 5.5 Elektromagnetické pole Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
2
 Modul Spájanie str. 1 Modul Spájanie Obsah: 1 Úvod 2 2 Prenos údajov spájanie 2 2.1.1 Generovanie údajov 3 2.1.2 Prenos údajov 4 2.1.3 Spájanie údajov 5 3 Poznámky 7 Modul Spájanie str. 2 1 Úvod Tento
Modul Spájanie str. 1 Modul Spájanie Obsah: 1 Úvod 2 2 Prenos údajov spájanie 2 2.1.1 Generovanie údajov 3 2.1.2 Prenos údajov 4 2.1.3 Spájanie údajov 5 3 Poznámky 7 Modul Spájanie str. 2 1 Úvod Tento
Metódy násobenie v stredoveku
 1 Lucia Pekarčíková História matematiky Metódy násobenia v stredoveku (Referát) Lucia Pekarčíková 1.roč. II.stupňa Mat Inf ÚVOD V dobe ranného stredoveku sa v Európe všeobecne nepoužíval abakus, nerobili
1 Lucia Pekarčíková História matematiky Metódy násobenia v stredoveku (Referát) Lucia Pekarčíková 1.roč. II.stupňa Mat Inf ÚVOD V dobe ranného stredoveku sa v Európe všeobecne nepoužíval abakus, nerobili
Zadanie_1_P1_TMII_ZS
 Grafické riešenie mechanizmov so súčasným pohybom DOMÁE ZDNIE - PRÍKLD č. Príklad.: Určte rýchlosti a zrýchlenia bodov,, a D rovinného mechanizmu na obrázku. v danej okamžitej polohe, ak je daná konštantná
Grafické riešenie mechanizmov so súčasným pohybom DOMÁE ZDNIE - PRÍKLD č. Príklad.: Určte rýchlosti a zrýchlenia bodov,, a D rovinného mechanizmu na obrázku. v danej okamžitej polohe, ak je daná konštantná
60. ročník Fyzikálnej olympiády v školskom roku 2018/2019 kategória E okresné kolo Riešenie úloh 1. Zohrievanie vody, výhrevnosť paliva a) Fosílne pal
 60. ročník Fyzikálnej olympiády v školskom roku 018/019 kategória E okresné kolo Riešenie úloh 1. Zohrievanie vody, výhrevnosť paliva a) Fosílne palivá: uhlie, nafta, olej, zemný plyn. Propán-bután, lieh,
60. ročník Fyzikálnej olympiády v školskom roku 018/019 kategória E okresné kolo Riešenie úloh 1. Zohrievanie vody, výhrevnosť paliva a) Fosílne palivá: uhlie, nafta, olej, zemný plyn. Propán-bután, lieh,
Programátorské etudy - Pascal
 MODIFIKÁCIA OBRÁZKOV ÚLOHA NA HODINU Dorobte projekt Modifikácia obrázkov, ktorý je zameraný na prácu s grafickou plochou ako dvojrozmerným poľom. Modifikáciu 13 máte predpripravenú. Doprogramujte ďalšie
MODIFIKÁCIA OBRÁZKOV ÚLOHA NA HODINU Dorobte projekt Modifikácia obrázkov, ktorý je zameraný na prácu s grafickou plochou ako dvojrozmerným poľom. Modifikáciu 13 máte predpripravenú. Doprogramujte ďalšie
gis5 prifuk
 Úrovne implementácie vektorového GIS. Eva Mičietová Univerzita Komenského v Bratislave Prírodovedecká fakulta Katedra kartografie, geoinformatiky a diaľkového prieskumu zeme Email: miciet@fns.uniba.sk
Úrovne implementácie vektorového GIS. Eva Mičietová Univerzita Komenského v Bratislave Prírodovedecká fakulta Katedra kartografie, geoinformatiky a diaľkového prieskumu zeme Email: miciet@fns.uniba.sk
WP summary
 TESTOVANIE PRAVDEPODOBNOSTNÉHO ROZDELENIA PREDIKČNÝCH CHÝB MARIÁN VÁVRA NETECHNICKÉ ZHRNUTIE 3/2018 Národná banka Slovenska www.nbs.sk Imricha Karvaša 1 813 25 Bratislava research@nbs.sk júl 2018 ISSN
TESTOVANIE PRAVDEPODOBNOSTNÉHO ROZDELENIA PREDIKČNÝCH CHÝB MARIÁN VÁVRA NETECHNICKÉ ZHRNUTIE 3/2018 Národná banka Slovenska www.nbs.sk Imricha Karvaša 1 813 25 Bratislava research@nbs.sk júl 2018 ISSN
SK MATEMATICKÁOLYMPIÁDA skmo.sk 63. ročník Matematickej olympiády 2013/2014 Riešenia úloh česko-poľsko-slovenského stretnutia 1. Dokážte, že kladné re
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 63. ročník Matematickej olympiády 2013/2014 Riešenia úloh česko-poľsko-slovenského stretnutia 1. Dokážte, že kladné reálne čísla a, b, c spĺňajú rovnicu a 4 + b 4 + c 4
SK MATEMATICKÁOLYMPIÁDA skmo.sk 63. ročník Matematickej olympiády 2013/2014 Riešenia úloh česko-poľsko-slovenského stretnutia 1. Dokážte, že kladné reálne čísla a, b, c spĺňajú rovnicu a 4 + b 4 + c 4
untitled
 Metódy na výpočet LS faktora pri modelovaní vodnej erózie pôdy Juraj Lieskovský UMB Banská Bystrica FPV kat. Krajinnej ekológie Banská Štiavnica juraj.lieskovsky@gmail.com Metódy na výpočet LS faktora
Metódy na výpočet LS faktora pri modelovaní vodnej erózie pôdy Juraj Lieskovský UMB Banská Bystrica FPV kat. Krajinnej ekológie Banská Štiavnica juraj.lieskovsky@gmail.com Metódy na výpočet LS faktora
Microsoft Word - Zaver.pisomka_januar2010.doc
 Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Matematika 2 - cast: Funkcia viac premenných
 Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
Paralelné algoritmy, cast c. 2
 Paralelné algoritmy, čast č. 2 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 2 Paralelné algoritmy,
Paralelné algoritmy, čast č. 2 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 2 Paralelné algoritmy,
Detekcia akustických udalostí v bezpečnostných aplikáciách
 TECHNICKÁ UNIVERZITA V KOŠICIACH FAKULTA ELEKTROTECHNIKY A INFORMATIKY KATEDRA ELEKTRONIKY AMULTIMEDIÁLNYCH TECHNOLÓGIÍ Metódy sledovania objektov vo videosekvenciách na báze geometrických vlastností Študijný
TECHNICKÁ UNIVERZITA V KOŠICIACH FAKULTA ELEKTROTECHNIKY A INFORMATIKY KATEDRA ELEKTRONIKY AMULTIMEDIÁLNYCH TECHNOLÓGIÍ Metódy sledovania objektov vo videosekvenciách na báze geometrických vlastností Študijný
Vhodnosť lokálneho ohodnocovania grafu v sociálnej sieti obchodného registra SR Peter Vojtek Mária Bieliková Fakulta informatiky a informačných techno
 Vhodnosť lokálneho ohodnocovania grafu v sociálnej sieti obchodného registra SR Peter Vojtek Mária Bieliková Fakulta informatiky a informačných technológií Slovenská technická univerzita v Bratislave Motivácia
Vhodnosť lokálneho ohodnocovania grafu v sociálnej sieti obchodného registra SR Peter Vojtek Mária Bieliková Fakulta informatiky a informačných technológií Slovenská technická univerzita v Bratislave Motivácia
Expertízny posudok stability drevín
 Dodávateľ: Ústav ekológie lesa SAV Zvolen Pobočka biológie drevín Nitra Akademická 2 949 01 Nitra Objednávateľ: Mesto Pezinok Radničné námestie 44/7 902 14 Pezinok EXPERTÍZNY POSUDOK Číslo objednávky:
Dodávateľ: Ústav ekológie lesa SAV Zvolen Pobočka biológie drevín Nitra Akademická 2 949 01 Nitra Objednávateľ: Mesto Pezinok Radničné námestie 44/7 902 14 Pezinok EXPERTÍZNY POSUDOK Číslo objednávky:
Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Pra
 Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Praktické programovanie assemblerových funkcií Autor:
Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Praktické programovanie assemblerových funkcií Autor:
Prenosový kanál a jeho kapacita
 Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Microsoft Word - Hitka - esej2011_06-is-xhitka.doc
 AKO VHODNE KOMBINOVAŤ SOFTVÉROVÉ METRIKY? Keď jedna metrika nestačí... Matúš Hitka Slovenská technická univerzita Fakulta informatiky a informačných technológií Ilkovičova 3, 842 16 Bratislava mhitka@gmail.com
AKO VHODNE KOMBINOVAŤ SOFTVÉROVÉ METRIKY? Keď jedna metrika nestačí... Matúš Hitka Slovenská technická univerzita Fakulta informatiky a informačných technológií Ilkovičova 3, 842 16 Bratislava mhitka@gmail.com
PL_2_2_vplyv_objemu
 Pokus 1 (Lapitková, et al., 2010, s. 78) Cieľ pokusu Preskúmať, ako vplýva objem a tvar telesa na hĺbku ponoru. Úloha č.1 Porovnaj hĺbku ponorenia dvoch škatúľ s rôznymi objemami, ak ich rovnako zaťažíš
Pokus 1 (Lapitková, et al., 2010, s. 78) Cieľ pokusu Preskúmať, ako vplýva objem a tvar telesa na hĺbku ponoru. Úloha č.1 Porovnaj hĺbku ponorenia dvoch škatúľ s rôznymi objemami, ak ich rovnako zaťažíš
STRUČNÝ NÁVOD KU IP-COACHU
 STRUČNÝ NÁVOD KU COACHU 5 Otvorenie programu a voľba úlohy na meranie Otvorenie programu Program IP- COACH na meranie otvoríme kliknutím na ikonu na obrazovke: Obr.1 Voľba úlohy na meranie Po kliknutí
STRUČNÝ NÁVOD KU COACHU 5 Otvorenie programu a voľba úlohy na meranie Otvorenie programu Program IP- COACH na meranie otvoríme kliknutím na ikonu na obrazovke: Obr.1 Voľba úlohy na meranie Po kliknutí
1. KOMPLEXNÉ ČÍSLA 1. Nájdite výsledok operácie v tvare x+yi, kde x, y R. a i (5 2i)(4 i) b. i(1 + i)(1 i)(1 + 2i)(1 2i) (1 7i) c. (2+3i) a+bi d
 KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
Microsoft Word - 1 Zakladne-pojmy
 1 ZÁKLADNÉ POJMY Predtým ako sa začneme systematcky zaoberať jednotlvým časťam aplkovanej fyzkálnej chéme, sa zoznámme so základným pojmam, ktorým budeme pracovať. 1.1 Hmota Úlohou prírodných ved, medz
1 ZÁKLADNÉ POJMY Predtým ako sa začneme systematcky zaoberať jednotlvým časťam aplkovanej fyzkálnej chéme, sa zoznámme so základným pojmam, ktorým budeme pracovať. 1.1 Hmota Úlohou prírodných ved, medz
STRUČNÝ NÁVOD KU IP-COACHU
 STRUČNÝ NÁVOD KU COACHU 6 Otvorenie programu a voľba úlohy na meranie Otvorenie programu Program COACH na meranie otvoríme kliknutím na ikonu Autor na obrazovke, potom zvolíme Užívateľskú úroveň Pokročilý
STRUČNÝ NÁVOD KU COACHU 6 Otvorenie programu a voľba úlohy na meranie Otvorenie programu Program COACH na meranie otvoríme kliknutím na ikonu Autor na obrazovke, potom zvolíme Užívateľskú úroveň Pokročilý
Novinky programu MSklad
 Novinky v programe MSklad 1.51 Poznámka v receptúre V receptúre je možné po novom pripísať ku každej položke poznámku, ktorá sa potom zobrazí pri tlači delenej žiadanky a voliteľne tiež pri tlači komplexnej
Novinky v programe MSklad 1.51 Poznámka v receptúre V receptúre je možné po novom pripísať ku každej položke poznámku, ktorá sa potom zobrazí pri tlači delenej žiadanky a voliteľne tiež pri tlači komplexnej
diplomovka2.doc
 nalýza zmen dôchodkového systému pomocou CE modelov Dplomová práca Monka Voteková Unverzta Komenského v Bratslave Fakulta matematky, fyzky a nformatky Katedra aplkovane matematky a štatstky 9.1.9 plkovaná
nalýza zmen dôchodkového systému pomocou CE modelov Dplomová práca Monka Voteková Unverzta Komenského v Bratslave Fakulta matematky, fyzky a nformatky Katedra aplkovane matematky a štatstky 9.1.9 plkovaná
Úlohy: Inteligentné modelovanie a riadenie model MR mobilný robot s diferenciálnym kolesovým podvozkom 1. Vytvorte simulačnú schému pre snímanie tréno
 Úlohy: Inteligentné modelovanie a riadenie model MR mobilný robot s diferenciálnym kolesovým podvozkom 1. Vytvorte simulačnú schému pre snímanie trénovacích a testovacích dát dopredného neurónového modelu
Úlohy: Inteligentné modelovanie a riadenie model MR mobilný robot s diferenciálnym kolesovým podvozkom 1. Vytvorte simulačnú schému pre snímanie trénovacích a testovacích dát dopredného neurónového modelu
Kolmogorovská zložitost
 Kolmogorovská zložitosť 5.12.2013 (2013/14) KZ 5.12.2013 1 / 16 Kt zložitosť age(x) = min p{2 l(p) t : U(p) = x v priebehu t krokov} Def. (Kt zložitosť) UTS monotonne skenuje začiatok p kým vypíše x, t(p,
Kolmogorovská zložitosť 5.12.2013 (2013/14) KZ 5.12.2013 1 / 16 Kt zložitosť age(x) = min p{2 l(p) t : U(p) = x v priebehu t krokov} Def. (Kt zložitosť) UTS monotonne skenuje začiatok p kým vypíše x, t(p,
M59dkZ9ri10
 MATEMATICKÁ OLYMPIÁDA Komentáre a riešenia úloh domáceho kola pre žiakov základných škôl a nižších ročníkov osemročných gymnázií Kategória Z9 59 ročník Školský rok 2009/2010 KATEGÓRIA Z9 Z9 I 1 Dostal
MATEMATICKÁ OLYMPIÁDA Komentáre a riešenia úloh domáceho kola pre žiakov základných škôl a nižších ročníkov osemročných gymnázií Kategória Z9 59 ročník Školský rok 2009/2010 KATEGÓRIA Z9 Z9 I 1 Dostal
Teória pravdepodobnosti Zákony velkých císel
 10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
TM Leica DISTO Leica DISTOTMD510 X310 The original laser distance meter The original laser distance meter
 TM Leca DISTO Leca DISTOTMD510 X10 The orgnal laser dstance meter The orgnal laser dstance meter Obsah Nastavene prístroja - - - - - - - - - - - - - - - - - - - - - - - - 2 Úvod - - - - - - - - - - - -
TM Leca DISTO Leca DISTOTMD510 X10 The orgnal laser dstance meter The orgnal laser dstance meter Obsah Nastavene prístroja - - - - - - - - - - - - - - - - - - - - - - - - 2 Úvod - - - - - - - - - - - -
PowerPoint Presentation
 Seminár Robotika.SK Ako naučiť robota vidieť ľudskú tvár pomocou knižnice Dlib Andrej Lúčny Katedra aplikovanej informatiky FMFI UK lucny@fmph.uniba.sk http://dai.fmph.uniba.sk/w/andrej_lucny www.robotika.sk/cviko7-faces.zip
Seminár Robotika.SK Ako naučiť robota vidieť ľudskú tvár pomocou knižnice Dlib Andrej Lúčny Katedra aplikovanej informatiky FMFI UK lucny@fmph.uniba.sk http://dai.fmph.uniba.sk/w/andrej_lucny www.robotika.sk/cviko7-faces.zip
Čo sú pojmové mapy 1 Charakterizácia pojmových máp pojmové mapy sú diagramy, ktoré vyjadrujú podstatné vzťahy medzi pojmami vo forme tvrdení. Tvrdenia
 Čo sú pojmové mapy 1 Charakterizácia pojmových máp pojmové mapy sú diagramy, ktoré vyjadrujú podstatné vzťahy medzi pojmami vo forme tvrdení. Tvrdenia sú v nich reprezentované stručne charakterizovanými
Čo sú pojmové mapy 1 Charakterizácia pojmových máp pojmové mapy sú diagramy, ktoré vyjadrujú podstatné vzťahy medzi pojmami vo forme tvrdení. Tvrdenia sú v nich reprezentované stručne charakterizovanými
SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE Fakulta informatiky a informačných technológií STU Ústav počítačových systémov a sietí ZADANIE SEMESTRÁLNE
 Riešitelia: Bc. Michal Behúň Názov projektu: Napájací zdroj ovládaný cez sériové rozhranie počítača Navrhnite a zrealizujte zdroj napätia od 0 do 10 V ovládaný cez sériové rozhranie počítača na báze mikropočítača
Riešitelia: Bc. Michal Behúň Názov projektu: Napájací zdroj ovládaný cez sériové rozhranie počítača Navrhnite a zrealizujte zdroj napätia od 0 do 10 V ovládaný cez sériové rozhranie počítača na báze mikropočítača
Telesá Príklady: 1) Vypočítajte objem a povrch pravidelného štvorbokého ihlana ak a = 10 cm s uhol ACV = 70 2) Kváder má rozmery a = 4 cm, b = 3 cm, c
 Príklady: 1) Vypočítajte objem a povrch pravidelného štvorbokého ihlana ak a = 10 cm s uhol ACV = 70 2) Kváder má rozmery a = 4 cm, b = 3 cm, c = 5 cm. Vypočítajte uhol α medzi podstavovou a telesovou
Príklady: 1) Vypočítajte objem a povrch pravidelného štvorbokého ihlana ak a = 10 cm s uhol ACV = 70 2) Kváder má rozmery a = 4 cm, b = 3 cm, c = 5 cm. Vypočítajte uhol α medzi podstavovou a telesovou
Informačné technológie
 Informačné technológie Piatok 15.11. 2013 Matúš Péči Barbora Zahradníková Soňa Duchovičová Matúš Gramlička Začiatok/Koniec Z K Vstup/Výstup A, B Načítanie vstupných premenných A, B resp. výstup výstupných
Informačné technológie Piatok 15.11. 2013 Matúš Péči Barbora Zahradníková Soňa Duchovičová Matúš Gramlička Začiatok/Koniec Z K Vstup/Výstup A, B Načítanie vstupných premenných A, B resp. výstup výstupných
Detektor kovu, napätia a dreva 3 v 1 DM-902 Každé kopírovanie, reprodukovanie a rozširovanie tohto návodu vyžaduje písomný súhlas firmy Transfer Multi
 Detektor kovu, napätia a dreva 3 v 1 DM-902 Každé kopírovanie, reprodukovanie a rozširovanie tohto návodu vyžaduje písomný súhlas firmy Transfer Multisort Elektronik. Návod na obsluhu Tento prístroj využíva
Detektor kovu, napätia a dreva 3 v 1 DM-902 Každé kopírovanie, reprodukovanie a rozširovanie tohto návodu vyžaduje písomný súhlas firmy Transfer Multisort Elektronik. Návod na obsluhu Tento prístroj využíva
IQ Easy firmy Simco-ION Nová generácia výrobkov pre ovládanie statickej elektriny SÚHRN: Firma Simco-ION predstavuje novú generáciu výrobkov pre elimi
 IQ Easy firmy Simco-ION Nová generácia výrobkov pre ovládanie statickej elektriny SÚHRN: Firma Simco-ION predstavuje novú generáciu výrobkov pre elimináciu statickej elektriny, elektrostatické nabíjanie
IQ Easy firmy Simco-ION Nová generácia výrobkov pre ovládanie statickej elektriny SÚHRN: Firma Simco-ION predstavuje novú generáciu výrobkov pre elimináciu statickej elektriny, elektrostatické nabíjanie
Paralelné algoritmy, cast c. 3
 Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2011/2012 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2011/2012 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Základné pravdepodobnostné modely v teórii spoľahlivosti
 Unverzta Komenského v Bratslave Fakulta Matematky, Fyzky a Informatky Katedra aplkovanej matematky a ²tatsktky tudjný odbor: 9.1.9 Aplkovaná matematka tudjný program: Ekonomcká a nan ná matematka Základné
Unverzta Komenského v Bratslave Fakulta Matematky, Fyzky a Informatky Katedra aplkovanej matematky a ²tatsktky tudjný odbor: 9.1.9 Aplkovaná matematka tudjný program: Ekonomcká a nan ná matematka Základné
Microsoft Word - Transparencies03.doc
 3. prednáška Teória množín II relácie o operácie nad reláciami o rovnosť o usporiadanosť funkcie o zložená funkcia o inverzná funkcia. Verzia: 20. 3. 2006 Priesvitka: 1 Relácie Definícia. Nech X a Y sú
3. prednáška Teória množín II relácie o operácie nad reláciami o rovnosť o usporiadanosť funkcie o zložená funkcia o inverzná funkcia. Verzia: 20. 3. 2006 Priesvitka: 1 Relácie Definícia. Nech X a Y sú
1 Portál pre odborné publikovanie ISSN Možnosti regulácie osvetlenia v programe Dialux Pavlík Marek Elektrotechnika V súčasne dob
 1 Portál pre odborné publikovanie ISSN 1338-0087 Možnosti regulácie osvetlenia v programe Dialux Pavlík Marek Elektrotechnika 22.05.2017 V súčasne dobe sa kladie čoraz väčší dôraz na šetrenie elektrickej
1 Portál pre odborné publikovanie ISSN 1338-0087 Možnosti regulácie osvetlenia v programe Dialux Pavlík Marek Elektrotechnika 22.05.2017 V súčasne dobe sa kladie čoraz väčší dôraz na šetrenie elektrickej
Snímka 1
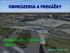 OBMEDZENIA A PREKÁŽKY Predpis L 14 I Letiská, hlava 4 Ing. Peter Koščák, PhD. Ochranné pásma letísk Legislatíva Zákon č. 143/1998 Z.z. o civilnom letectve Oddelenie OP letísk a LPZ Zákon č. 50/1976 Zb.
OBMEDZENIA A PREKÁŽKY Predpis L 14 I Letiská, hlava 4 Ing. Peter Koščák, PhD. Ochranné pásma letísk Legislatíva Zákon č. 143/1998 Z.z. o civilnom letectve Oddelenie OP letísk a LPZ Zákon č. 50/1976 Zb.
Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, prič
 Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, pričom to je veľmi dôležitá súčasť úlohy. Body sa udeľovali
Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, pričom to je veľmi dôležitá súčasť úlohy. Body sa udeľovali
fadsgasga
 Základná geometria, Reprezentácia objektov Júlia Kučerová Úloha počítačovej grafiky Základy počítačovej grafiky a spracovanie obrazu 2015/2016 2 Referenčný model PG Aplikačný program Grafický systém Grafické
Základná geometria, Reprezentácia objektov Júlia Kučerová Úloha počítačovej grafiky Základy počítačovej grafiky a spracovanie obrazu 2015/2016 2 Referenčný model PG Aplikačný program Grafický systém Grafické
Expertízny posudok stability drevín
 Dodávateľ: Ústav ekológie lesa SAV Zvolen Pobočka biológie drevín Nitra Akademická 2 949 01 Nitra Objednávateľ: Mesto Pezinok Radničné námestie 7 902 14 Pezinok EXPERTÍZNY POSUDOK Objednávka č. 20180252/2018
Dodávateľ: Ústav ekológie lesa SAV Zvolen Pobočka biológie drevín Nitra Akademická 2 949 01 Nitra Objednávateľ: Mesto Pezinok Radničné námestie 7 902 14 Pezinok EXPERTÍZNY POSUDOK Objednávka č. 20180252/2018
Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 2017 Definície Žena - objekt ohodnotený celým číslom. Každé dve ženy sa dajú porovnat a
 Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 207 Definície Žena - objekt ohodnotený celým číslom. aždé dve ženy sa dajú porovnat a rozlíšit, t.j. žiadne dve nemajú rovanké hodnotenie.
Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 207 Definície Žena - objekt ohodnotený celým číslom. aždé dve ženy sa dajú porovnat a rozlíšit, t.j. žiadne dve nemajú rovanké hodnotenie.
kde parametre α a β vyjadrujú elasticitu \(pružnosť\) produkcie y vo vzťahu k činiteľom F a Z, t.j. relatívny prírastok p...
 8 Produkčné modely 9 8 Produkčné modely Ekonometrcké modely produkce sa zameravajú na skúmane ekonomckých závslostí, ktoré sa važu na tvorbu nových hmotných statkov. Pr zodpovedajúcej modfkác možno formulu
8 Produkčné modely 9 8 Produkčné modely Ekonometrcké modely produkce sa zameravajú na skúmane ekonomckých závslostí, ktoré sa važu na tvorbu nových hmotných statkov. Pr zodpovedajúcej modfkác možno formulu
17. medzinárodná vedecká konferencia Riešenie krízových situácií v špecifickom prostredí, Fakulta špeciálneho inžinierstva ŽU, Žilina, máj 2
 17. medzinárodná vedecká konferencia Riešenie krízových situácií v špecifickom prostredí, Fakulta špeciálneho inžinierstva ŽU, Žilina, 30. - 31. máj 2012 ZÁSOBOVANIE VRTUĽNÍKOV VYUŽÍVANÝCH PRI RIEŠENÍ
17. medzinárodná vedecká konferencia Riešenie krízových situácií v špecifickom prostredí, Fakulta špeciálneho inžinierstva ŽU, Žilina, 30. - 31. máj 2012 ZÁSOBOVANIE VRTUĽNÍKOV VYUŽÍVANÝCH PRI RIEŠENÍ
Študijný program (Študijný odbor) Školiteľ Forma štúdia Téma Elektronické zbraňové systémy (8.4.3 Výzbroj a technika ozbrojených síl) doc. Ing. Martin
 doc. Ing. Martin Marko, CSc. e-mail: martin.marko@aos.sk tel.: 0960 423878 Metódy kódovania a modulácie v konvergentných bojových rádiových sieťach Zameranie: Dizertačná práca sa bude zaoberať modernými
doc. Ing. Martin Marko, CSc. e-mail: martin.marko@aos.sk tel.: 0960 423878 Metódy kódovania a modulácie v konvergentných bojových rádiových sieťach Zameranie: Dizertačná práca sa bude zaoberať modernými
Microsoft Word - MAT_2018_1 kolo.docx
 Gymnázium Pavla Horova, Masarykova 1, Michalovce Príklady na prijímacie skúšky do 1. ročníka konané dňa 14. mája 2018 MATEMATIKA V úlohách 1) až 8) je práve jedna odpoveď správna. Túto správnu odpoveď
Gymnázium Pavla Horova, Masarykova 1, Michalovce Príklady na prijímacie skúšky do 1. ročníka konané dňa 14. mája 2018 MATEMATIKA V úlohách 1) až 8) je práve jedna odpoveď správna. Túto správnu odpoveď
Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovsk
 Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovská cesta 1, 034 01 Ružomberok, Slovakia e-mail: marian.trenkler@ku.sk
Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovská cesta 1, 034 01 Ružomberok, Slovakia e-mail: marian.trenkler@ku.sk
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/ ročník Matematickej olympiády Riešenia úloh IMO 1. Určte všetky funkcie f: R R také, že rovnosť f ( x y
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/2010 59. ročník Matematickej olympiády Riešenia úloh IMO 1. Určte všetky funkcie f: R R také, že rovnosť f ( x y ) = f(x) f(y) platí pre všetky x, y R. (Symbol z označuje
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/2010 59. ročník Matematickej olympiády Riešenia úloh IMO 1. Určte všetky funkcie f: R R také, že rovnosť f ( x y ) = f(x) f(y) platí pre všetky x, y R. (Symbol z označuje
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Zachovanie mentálnej mapy hrán pri interakcii s grafom Diplomová práca Bra
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Zachovanie mentálnej mapy hrán pri interakcii s grafom Diplomová práca Bratislava, 2013 Bc. Martin Ďuriš Univerzita Komenského
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Zachovanie mentálnej mapy hrán pri interakcii s grafom Diplomová práca Bratislava, 2013 Bc. Martin Ďuriš Univerzita Komenského
Manažment v Tvorbe Softvéru 2018/2019
 (dokonč.) MTS 2018/19 I. M. rozsahu projektu II. M. rozvrhu projektu III. M. nákladov projektu rozsahu rozvrhu Definovanie činností nákladov Získanie požiadaviek Zoradenie činností Odhad trvania činností
(dokonč.) MTS 2018/19 I. M. rozsahu projektu II. M. rozvrhu projektu III. M. nákladov projektu rozsahu rozvrhu Definovanie činností nákladov Získanie požiadaviek Zoradenie činností Odhad trvania činností
1 Portál pre odborné publikovanie ISSN Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika
 1 Portál pre odborné publikovanie ISSN 1338-0087 Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika 28.04.2010 Článok spočíva v predstavení a opísaní algoritmu
1 Portál pre odborné publikovanie ISSN 1338-0087 Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika 28.04.2010 Článok spočíva v predstavení a opísaní algoritmu
VZTAH STUDENTŮ VŠ K DISCIPLÍNÁM TEORETICKÉ INFORMATIKY
 5. vedecká konferencia doktorandov a mladých vedeckých pracovníkov LIMITA A DERIVÁCIA FUNKCIE UKÁŽKA KVANTITATÍVNEHO VÝSKUMU Ján Gunčaga The present paper is devoted to a qualitative research related to
5. vedecká konferencia doktorandov a mladých vedeckých pracovníkov LIMITA A DERIVÁCIA FUNKCIE UKÁŽKA KVANTITATÍVNEHO VÝSKUMU Ján Gunčaga The present paper is devoted to a qualitative research related to
PoĊítaĊová sieť
 Počítačová sieť Def. 1: Systém vzájomne prepojených a spolupracujúcich PC Def. 2 Skupina PC (minimálne dvoch), ktoré sú navzájom prepojené takým spôsobom, že je možný prenos dát medzi nimi. Druhy počítačov
Počítačová sieť Def. 1: Systém vzájomne prepojených a spolupracujúcich PC Def. 2 Skupina PC (minimálne dvoch), ktoré sú navzájom prepojené takým spôsobom, že je možný prenos dát medzi nimi. Druhy počítačov
Axióma výberu
 Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Leica DISTO TM S910 The original laser distance meter
 Leca DISTO TM S910 The orgnal laser dstance meter Obsah Nastavene prístroja - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 Úvod - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Leca DISTO TM S910 The orgnal laser dstance meter Obsah Nastavene prístroja - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 Úvod - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1
 ADM a logika 5. prednáška Sémantické tablá priesvitka 1 Úvodné poznámky Cieľom dnešnej prednášky je moderná sémantická metóda verifikácie skutočnosti, či formula je tautológia alebo kontradikcia: Metóda
ADM a logika 5. prednáška Sémantické tablá priesvitka 1 Úvodné poznámky Cieľom dnešnej prednášky je moderná sémantická metóda verifikácie skutočnosti, či formula je tautológia alebo kontradikcia: Metóda
