Základy automatického riadenia - Prednáška 2
|
|
|
- Stanislava Urbanová
- pred 4 rokmi
- Prehliadani:
Prepis
1 Základy automatického riadenia Predná²ka 2 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita v Ko²iciach LS 2015/2016 (TUKE) Základy automatického riadenia LS 2015/ / 30
2 Denícia Systém je objekt s denovanými veli inami a denovanými vz ahmi medzi nimi. Deterministický jednorozmerný systém je denovaný na skúmanom objekte tak, ºe na z okolia pôsobí vstupná veli ina u(t) a výsledkom tohto pôsobenia je pozorovate ná, výstupná veli ina y(t), pri om pri rovnakých po iato ných podmienkach k ur itej veli ine u(t) je priradená vºdy tá istá veli ina y(t). Nezávislá premenná je as t. Pri dynamických systémoch so sústredenými parametrami sú vz ahy medzi vstupnými a výstupnými veli inami opísané pomocou oby ajných diferenciálnych rovníc a deriváciami pod a asu. (TUKE) Základy automatického riadenia LS 2015/ / 30
3 Zákon superpozície Lineárne systémy sú také systémy, pre ktoré platí zákon superpozície. Tento zákon moºno vyjadri rovnicou y = T (a 1 u 1 + a 2 u 2 ) kde T je lineárny operátor a a 1, a 2 sú reálne ísla. = a 1 T (u 1 ) + a 2 T (u 2 ) = a 1 y 1 + a 2 y 2 (1) Ak pre proces denujeme z h adiska priestoru a asu súbor typicky významných vlastností, dôleºitých pre cie ná²ho skúmania, potom hovoríme, ºe sme na objekte - procese denovali systém. (TUKE) Základy automatického riadenia LS 2015/ / 30
4 Klasikácia systémov Dynamické systémy so sústredenými parametrami so rozloženými parametrami lineárne nelineárne deterministické stochastické s konštantnými parametrami s premenlivými parametrami diskrétne spojité (TUKE) Základy automatického riadenia LS 2015/ / 30
5 Základné charakteristiky Matematický opis lineárnych spojitých systémov je moºné vyjadri pomocou dvoch ekvivalentných opisov: vonkaj²í opis - opis pomocou vstupno-výstupných premenných - diferenciálne rovnice, obrazové prenosy vnútorný opis - opis pomocou vnútorných premenných Ak poznáme vnútorný popis (model) LDS, jednozna ne z neho vyplýva aj vonkaj²í opis (V/V opis) LDS. (TUKE) Základy automatického riadenia LS 2015/ / 30
6 Vonkaj²í matematický opis spojitých LDS systémov Spojitý LDS je moºné popísa lineárnou diferenciálnou rovnicou: a n y (n) (t) a 1 y (t) + a 0 y(t) = b m u (m) (t) b 1 u (t) + b 0 u(t) kde a 0, a 1,..., a n, b 0, b 1,..., b m sú kon²tantné koecienty y(t) je výstup LDS u(t) je vstup LDS podmienka fyzikálnej realizovate nosti: n m (TUKE) Základy automatického riadenia LS 2015/ / 30
7 Pri získavaní modelu LDS (odvodenie LDR) vychádzame z fyzikálnej podstaty dejom skúmaného LDS. Vonkaj²í (V/V) opis LDS: model v tvare LDS obrazový prenos v LT frekven ný prenos prechodová charakteristika, impulzná charakteristika, frekven ná charakteristika Vnútorný opis LDS: metóda stavového priestoru (úplný obraz o v²etkých dynamických vlastnostiach lineárneho systému) Metódy zaloºené na stavovom priestore pracujú v t-oblasti. (TUKE) Základy automatického riadenia LS 2015/ / 30
8 Laplaceova transformácia Laplaceova transformácia poskytuje ve mi jednoduchú metódu rie²enia lineárnych diferenciálnych rovníc vhodná na odvodenie vstupno-výstupných modelov, ktorých pouºitie je výhodné pri identikácii alebo návrhu algoritmov riadenia Laplaceova transformácia je daná vz ahom L{f (t)} 0 f (t) e st Funkciu f (t) nazývame originálom a funkciu F (s) jej obrazom. (TUKE) Základy automatického riadenia LS 2015/ / 30
9 Eulerove vzorce Pre praktické výpo ty pomocou Laplaceovej transformácie sú uºito né pomocné vz ahy(eulerove vzorce): cos(ωt) = ei ωt + e i ωt, sin(ωt) = ei ωt e i ωt, 2 2 i e i ωt = cos(ωt) + i sin(ωt), e i ωt = cos(ωt) i sin(ωt). Základné vlastnosti Laplaceovej transformácie: originál obraz linearita k 1 f 1 ± k 2 f 2 k 1 F 1 ± k 2 F 2 substitúcia f (at) 1/aF (s/a) posun v origináli f (t a) e at F (s) posun v obraze e at f (t) F (s + a) (TUKE) Základy automatického riadenia LS 2015/ / 30
10 Obrazový prenos Obrazový prenos LDS je denovaný ako pomer obrazu Y(s) výstupnej veli iny y(t) ku obrazu U(s) vstupnej veli iny u(t): F (s) = Y (s) U(s) Popis LDS s pomocou obrazového prenosu SISO systém, SIMO systém, MIMO systém (TUKE) Základy automatického riadenia LS 2015/ / 30
11 Obrazový prenos Prenos systému je podiel obrazu výstupu ku obrazu vstupu pri nulových po iato ných podmienkach: L{y(t)} = L f (τ)u(t τ)dτ 0 y(t)e st = f (τ)u(t τ)dτ e st 0 0 ξ = t τ t = t + ξ = dξ Y (s) = f (τ)u(ξ)dτ e sτ e sξ dξ = = f (τ)e sτ dτ } {{ } F (s) 0 0 u(ξ)e sξ dξ = F (s)u(s) } {{ } U(s) F (s) = Y (s) U(s) Y (s) = F (s)u(s) (2) (TUKE) Základy automatického riadenia LS 2015/ / 30
12 Obrazový prenos Funk ný vz ah medzi vstupnou a výstupnou veli inou uvaºovaného systému je daný nasledovnou diferenciálnou rovnicou: a 2 y (t) + a 1 y (t) + a 0 y(t) = ku(t) (3) Za predpokladu, ºe sústava je v rovnováºnom stave, teda po iato né podmienky sú nulové (y(0) = 0, y (0) = 0), pouºitím LT môºeme písa : odkia obrazový prenos je: a 2 s 2 Y (s) + a 1 sy (s) + a 0 Y (s) = ku(s), (4) F (s) = Y (s) U(s) = k a 2 s 2 + a 1 s + a 0 (5) (TUKE) Základy automatického riadenia LS 2015/ / 30
13 Obrazový prenos V²eobecne môºeme obrazový prenos F (s) zapísa v tvare: F (s) = Y (s) U(s) = b ms m + b m 1 s m b 0 a n s n + a n 1 s n a 0 (6) Korene polynómu itate a ozna ujeme ako nuly a korene polynómu menovate a ako póly. Polynóm menovate a rovný nule sa volá charakteristická rovnica. (TUKE) Základy automatického riadenia LS 2015/ / 30
14 Príklady systémov prvého rádu - elektrický systém Elektrický systém vstup u 1 (t) výstup u 2 (t) Úloha: Nájdite v ah medzi vstupom a výstupom u 2 (t) = f (u 1 (t)) (TUKE) Základy automatického riadenia LS 2015/ / 30
15 Príklady systémov prvého rádu - elektrický systém Ak R 1 a C 1 sú ideálne (nemenia svoje hodnoty v závislosti od teploty, prúdu), systém je LINEÁRNY Pod a 1. a 2. Kirchhoovho zákona platí: u 1 (t) = R 1 i 1 (t)+u 2 (t), i 1 (t) = i 2 (t)+i c (t), i 2 (t) = 0 i 1 (t) = i c (t) a prúd te úci kondenzátorom môºeme vyjadri v tvare: i c = i 1 = C 1 du 2 u 1 = R 1 C 1 du 2 + u 2 (TUKE) Základy automatického riadenia LS 2015/ / 30
16 Príklady systémov prvého rádu - elektrický systém Ozna ením R 1 C 1 = T 1 dostávame nehomogénnu diferenciálnu rovnicu 1. rádu: T 1 du 2 + u 2 = u 1 Rie²enie uvedenej diferenciálnej rovnice sa skladá z rie²enia homogénnej dif. rovnice a partikulárneho rie²enia dif. rovnice: homogénnej rovnici T 1 du 2 + u 2 = 0 prislúcha rie²enie: u 2h = K 1 e st, u 2h (t) = K 1 e t T 1 kde s = 1/T 1 pre partikulárne rie²enie platí: nech u 1 (t) = u 1K, potom rie²enie má tvar u 2n (t) = K 2 a po dosadení do rovnice: T K 2 = u 1K ur íme kon²tantu K 2 = u 1K, u 2n (t) = u 1K (TUKE) Základy automatického riadenia LS 2015/ / 30
17 Príklady systémov prvého rádu - elektrický systém Výsledné rie²enie diferenciálnej rovnice: u 2 (t) = u 2h (t) + u 2n (t) = K 1 e t T 1 Kon²tantu K 1 ur íme z po iato ných podmienok: + u 1K u 2 (0) = 0 0 = K 1 e t/t 1 +u 1k K 1 = u 1K u 2 (t) = u 1k (1 e t T 1 ) Gracký priebeh rie²enia diferenciálnej rovnice pomocou analytických metód: (TUKE) Základy automatického riadenia LS 2015/ / 30
18 Elektrický systém prvého rádu (TUKE) Základy automatického riadenia LS 2015/ / 30
19 Elektrický systém prvého rádu Rie²enie pomocou Laplaceovej transformácie Nech u 1 (t) = u 1K, u 1 (0) = 0 du 2 (t) T 1 +u 2 (t) = u 1 (t) prepis do LT T 1 U 2 (s)s+u 2 (s) = u 1K s pri om Laplaceov obraz výstupnej veli iny: U 2 (s) = u 1 (t) U 1 (s) = u 1K s u 1K s(t 1 s + 1) = A s + B T 1 s + 1, A = u 1K, B = u 1K T 1 U 2 (s) = u 1K ( 1 s T 1 T 1 s + 1 ) (TUKE) Základy automatického riadenia LS 2015/ / 30
20 Elektrický systém prvého rádu Po prevode do asovej oblasti: u 2 (t) = u 1k (1 e t T 1 ) Gracký priebeh rie²enia diferenciálnej rovnice pomocou Laplaceovej transformácie: (TUKE) Základy automatického riadenia LS 2015/ / 30
21 Elektrický systém prvého rádu Jednokapacitný prenos Transformáciou diferenciálnej rovnice pri nulových po. podmienkach: T 1 du 2 (t) na Laplaceov obrazový prenos dostávame: + u 2 (t) = u 1 (t) T 1 U 2 (s)s + U 2 (s) = U 1 (s) a následnou úpravou získame Laplaceov obrazový prenos jednokapacitnej sústavy: F (s) = U 2(s) U 1 (s) = 1 T 1 s + 1 (TUKE) Základy automatického riadenia LS 2015/ / 30
22 Hydraulický systém prvého rádu Hydraulický systém prvého rádu vstup q 1 (t) - prítok média do nádoby výstup q 2 (t) - mnoºstvo vytekajúceho média z nádoby výstup h 1 (t) - vý²ka hladiny v nádobe S 1 - prierez nádoby, R 1 - hydr. odpor, γ - ²pecická váha kvapaliny Úloha 1: Nájdite vz ah medzi vstupom a výstupom q 2 (t) = f 1 (q 1 (t)) Úloha 2: Nájdite vz ah medzi vstupom a výstupom h 1 (t) = f 2 (q 1 (t)) (TUKE) Základy automatického riadenia LS 2015/ / 30
23 Hydraulický systém prvého rádu Bilan ná rovnica d(kvapaliny) = prítok ook dh 1 (t) S 1 = q 1 (t) q 2 (t) (TUKE) Základy automatického riadenia LS 2015/ / 30
24 Hydraulický systém prvého rádu Úloha 1 Výstup q 2 (t) - priamo úmerný hydraulickému tlaku v mieste odporu R 1, nepriamo úmerný odporu R 1 a lineárne závislý od vý²ky hladiny h 1 (t): q 2 (t) = γ R 1 h 1 (t) kde γ je ²pecická váha kvapaliny vytekajúca cez hydraulický odpor R 1 Deriváciou dostávame: dq 2 (t) = γ R 1 dh 1 (t) dh 1(t) = R 1 γ dq 2 (t) (TUKE) Základy automatického riadenia LS 2015/ / 30
25 Hydraulický systém prvého rádu Úloha 1 Dosadením do pôvodnej diferenciálnej rovnice dostaneme: S 1 R 1 γ dq 2 (t) + q 2 (t) = q 1 (t) Ozna ením S 1R 1 γ = T 1 sme získali LDR I. rádu. Výsledná diferenciálna rovnica pre hydraulický systém: T 1 dq 2 (t) + q 2 (t) = q 1 (t), ktorej rie²ením je: q 2 (t) = q 1 (1 e t T 1 ) o je rovnako ako v predo²lom príklade tvar rie²enia pre jednokapacitný prenos. (TUKE) Základy automatického riadenia LS 2015/ / 30
26 Hydraulický systém prvého rádu Úloha 2a: lineárny prípad, h 1(t) = f (q 1(t)) Ak chceme rie²i úlohu h 1 (t) = f (q 1 (t)), dosadíme do výsledného bilan ného vz ahu: dh 1 (t) S 1 = q 1 (t) q 2 (t) za q 2 (t) = γh 1(t) R 1 : S 1 dh 1 (t) a následnou úpravou dostávame LDR: S 1 dh 1 (t) = q 1 (t) γh 1(t) R 1 + γ R 1 h 1 (t) = q 1 (t), ktorej postup rie²enia je totoºný s uº uvedenými príkladmi. (TUKE) Základy automatického riadenia LS 2015/ / 30
27 Hydraulický systém prvého rádu Úloha 2b: nelineárny prípad Ak pre výtok kvapaliny z nádoby platí: q 2 (t) = k 1 f 2gh 1 (t), kde k 1 - kon²t., f - priemer výtokového otvoru, g - gravita né zrýchlenie Ozna ením k 2 = k 1 f 2g a dosadením do výslednej bilan nej rovnice: S 1 dh 1 (t) = q 1 (t) q 2 (t) dostávame nelineárnu diferenciálnu rovnicu (NDR): S 1 dh 1 (t) + k 2 h1 (t) = q 1 (t), NDR nevieme rie²i analyticky v t-oblasti oblasti, ani pomocou Laplaceovej transformácie. (TUKE) Základy automatického riadenia LS 2015/ / 30
28 Hydraulický systém prvého rádu Úloha 2b: nelineárny prípad (TUKE) Základy automatického riadenia LS 2015/ / 30
29 Hydraulický systém prvého rádu Úloha 2b: nelineárny prípad, linearizácia Linearizácia rozvoj do Taylorovho radu: q 2 (t) q 2 (h1) 0 + q 2(h 1) (h 1(t) h 0) ! pri om platí: q 2 (h 0) = k 1 2 h 0, 1 q 2 (h0) = k h 0 = k 1 h dosadením do rovnice dostávame: q 2 (t) k 2 h k 2 q 2 (t) k 2 h h 0 1 2h k 2 2 (h 1 (t) h 0 1) h 0 1 2h 0 1 h 1 (t) 2h 0 1 (TUKE) Základy automatického riadenia LS 2015/ / 30
30 Hydraulický systém prvého rádu Úloha 2b: nelineárny prípad Ozna ením: k 3 = k 2 h 0 1 dostávame výsledný hydraulický model vyjadrený LDR: S 1 dh 1 (t) 2 + k 3 h h 0 1 (t) = q 1 (t) k 3, 1 ktorú vieme rie²i metódami uvedenými v predo²lých príkladoch. (TUKE) Základy automatického riadenia LS 2015/ / 30
Slide 1
 Diferenciálne rovnice Základný jazyk fyziky Motivácia Typická úloha fyziky hľadanie časových priebehov veličín, ktoré spĺňajú daný fyzikálny zákon. Určte trajektóriu telesa rt ( )???? padajúceho v gravitačnom
Diferenciálne rovnice Základný jazyk fyziky Motivácia Typická úloha fyziky hľadanie časových priebehov veličín, ktoré spĺňajú daný fyzikálny zákon. Určte trajektóriu telesa rt ( )???? padajúceho v gravitačnom
prednaska
 Úvod do nelineárnych systémov doc. Ing. Anna Jadlovská, PhD. ZS 2016 Prednáška 1 1.1 Stručné zopakovanie pojmov z LDS Uvažujme lineárny t-invariantný DS n-tého rádu (LDS): pričom x(t) 2 R n, u(t) 2 R n,
Úvod do nelineárnych systémov doc. Ing. Anna Jadlovská, PhD. ZS 2016 Prednáška 1 1.1 Stručné zopakovanie pojmov z LDS Uvažujme lineárny t-invariantný DS n-tého rádu (LDS): pričom x(t) 2 R n, u(t) 2 R n,
Zadání čtvrté série
 Pomocný text Vektory V na²om pomocnom texte Vás prevedieme postupne afínnou geometriou, skalárnym sú inom dvoch vektorov, vektorovým sú inom a zmienime sa krátko o orientovanom obsahu a jeho vyuºití. Tento
Pomocný text Vektory V na²om pomocnom texte Vás prevedieme postupne afínnou geometriou, skalárnym sú inom dvoch vektorov, vektorovým sú inom a zmienime sa krátko o orientovanom obsahu a jeho vyuºití. Tento
Microsoft Word - 6 Výrazy a vzorce.doc
 6 téma: Výrazy a vzorce I Úlohy na úvod 1 1 Zistite definičný obor výrazu V = 4 Riešte sústavu 15 = 6a + b, = 4a c, 1 = 4a + b 16c Rozložte na súčin výrazy a) b 4 a 18, b) c 5cd 10c d +, c) 6 1 s + z 4
6 téma: Výrazy a vzorce I Úlohy na úvod 1 1 Zistite definičný obor výrazu V = 4 Riešte sústavu 15 = 6a + b, = 4a c, 1 = 4a + b 16c Rozložte na súčin výrazy a) b 4 a 18, b) c 5cd 10c d +, c) 6 1 s + z 4
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom
 2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
Príspevok k modelovaniu a riadeniu robotických systémov s využitím metód umelej inteligencie
 PRÍSPEVOK K HYBRIDNÝM MODELOM KYBER-FYZIKÁLNYCH SYSTÉMOV A ICH IMPLEMENTÁCIA DO DISTRIBUOVANÉHO SYSTÉMU RIADENIA TUKE FEI KKUI školiteľ: Ing. Dominik Vošček doc. Ing. Anna Jadlovská, PhD. 14.3.2017 ČLENENIE
PRÍSPEVOK K HYBRIDNÝM MODELOM KYBER-FYZIKÁLNYCH SYSTÉMOV A ICH IMPLEMENTÁCIA DO DISTRIBUOVANÉHO SYSTÉMU RIADENIA TUKE FEI KKUI školiteľ: Ing. Dominik Vošček doc. Ing. Anna Jadlovská, PhD. 14.3.2017 ČLENENIE
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Ekonomická a nan ná matematika Asymptotické metódy oce ovania ázijských ty
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Ekonomická a nan ná matematika Asymptotické metódy oce ovania ázijských typov nan ných derivátov DIPLOMOVÁ PRÁCA Diplomant: Lenka
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Ekonomická a nan ná matematika Asymptotické metódy oce ovania ázijských typov nan ných derivátov DIPLOMOVÁ PRÁCA Diplomant: Lenka
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA A NÁVRH NUMERICKÝCH ALGORITMOV NA RIE ENIE NELINEÁRNYCH ROVNÍC BLA
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA A NÁVRH NUMERICKÝCH ALGORITMOV NA RIE ENIE NELINEÁRNYCH ROVNÍC BLACK - SCHOLESOVHO TYPU DIPLOMOVÁ PRÁCA 2012 Bc. Jana
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA A NÁVRH NUMERICKÝCH ALGORITMOV NA RIE ENIE NELINEÁRNYCH ROVNÍC BLACK - SCHOLESOVHO TYPU DIPLOMOVÁ PRÁCA 2012 Bc. Jana
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) Matematická analýza IV (ÚMV/MAN2d/10) RNDr. Lenka Halčinová, PhD.
 III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
Axióma výberu
 Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Základné stochastické procesy vo financiách
 Technická Univerzita v Košiciach Ekonomická fakulta 20. Január 2012 základné charakteristiky zmena hodnoty W t simulácia WIENEROV PROCES základné charakteristiky základné charakteristiky zmena hodnoty
Technická Univerzita v Košiciach Ekonomická fakulta 20. Január 2012 základné charakteristiky zmena hodnoty W t simulácia WIENEROV PROCES základné charakteristiky základné charakteristiky zmena hodnoty
9. Elastické vlastnosti kry²tálov Cie om tejto predná²ky je zhrnú základné poznatky z mechaniky kontinua. Úlohou je ur i, ako sa deformuje daný kus lá
 9. Elastické vlastnosti kry²tálov Cie om tejto predná²ky je zhrnú základné poznatky z mechaniky kontinua. Úlohou je ur i, ako sa deformuje daný kus látky pri zadaných mechanických pôsobeniach. Budeme predpoklada,
9. Elastické vlastnosti kry²tálov Cie om tejto predná²ky je zhrnú základné poznatky z mechaniky kontinua. Úlohou je ur i, ako sa deformuje daný kus látky pri zadaných mechanických pôsobeniach. Budeme predpoklada,
Operačná analýza 2
 Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Prenosový kanál a jeho kapacita
 Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú in
 Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Lorentzova sila a jej (zov²eobecnená") potenciálna energia Marián Fecko KTF&DF, FMFI UK, Bratislava Na predná²ke sme sa dozvedeli, ºe Lorentzova sila
 Lorentzova sila a jej (zov²eobecnená") potenciálna energia Marián Fecko KTF&DF, FMFI UK, Bratislava Na predná²ke sme sa dozvedeli, ºe Lorentzova sila (pôsobiaca na bodový náboj e v danom elektrickom a
Lorentzova sila a jej (zov²eobecnená") potenciálna energia Marián Fecko KTF&DF, FMFI UK, Bratislava Na predná²ke sme sa dozvedeli, ºe Lorentzova sila (pôsobiaca na bodový náboj e v danom elektrickom a
MO_pred1
 Modelovanie a optimalizácia Ľudmila Jánošíková Katedra dopravných sietí Fakulta riadenia a informatiky Žilinská univerzita, Žilina Ludmila.Janosikova@fri.uniza.sk 041/5134 220 Modelovanie a optimalizácia
Modelovanie a optimalizácia Ľudmila Jánošíková Katedra dopravných sietí Fakulta riadenia a informatiky Žilinská univerzita, Žilina Ludmila.Janosikova@fri.uniza.sk 041/5134 220 Modelovanie a optimalizácia
BRKOS
 Pomocný text Výroková logika autor: Viki Logika je nástroj, ktorý nám umoº uje matematicky uvaºova o veciach okolo nás. Dovo uje nám formalizova tvrdenia, ktoré chceme dokáza a zárove formalizova samotný
Pomocný text Výroková logika autor: Viki Logika je nástroj, ktorý nám umoº uje matematicky uvaºova o veciach okolo nás. Dovo uje nám formalizova tvrdenia, ktoré chceme dokáza a zárove formalizova samotný
Teória pravdepodobnosti Zákony velkých císel
 10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
O možnosti riešenia deformácie zemského povrchu z pohladu metódy konecných prvkov konference pro studenty matematiky
 O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Podobnos slov (Diplomová práca) Martin Vl ák Vedúci: RN
 Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Podobnos slov (Diplomová práca) Martin Vl ák Vedúci: RNDr. Michal Forí²ek Phd. Bratislava, 2011 ii Martin
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Podobnos slov (Diplomová práca) Martin Vl ák Vedúci: RNDr. Michal Forí²ek Phd. Bratislava, 2011 ii Martin
Biharmonická rovnica - ciže co spôsobí pridanie jedného laplasiánu
 iºe o spôsobí pridanie jedného laplasiánu tyc struna Obsah ƒo je to biharmonická rovnica 2 Malý výlet do teórie pruºnosti 3 Rovnice, okrajové podmienky, rie²enia 4... a kde ostala matematická fyzika? ƒo
iºe o spôsobí pridanie jedného laplasiánu tyc struna Obsah ƒo je to biharmonická rovnica 2 Malý výlet do teórie pruºnosti 3 Rovnice, okrajové podmienky, rie²enia 4... a kde ostala matematická fyzika? ƒo
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BAKALÁRSKA PRÁCA Bratislava 2011 Roman Kukumberg
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BAKALÁRSKA PRÁCA Bratislava 2011 Roman Kukumberg Proximal-gradient, metóda konvexného programovania BAKALÁRSKA PRÁCA Roman Kukumberg
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BAKALÁRSKA PRÁCA Bratislava 2011 Roman Kukumberg Proximal-gradient, metóda konvexného programovania BAKALÁRSKA PRÁCA Roman Kukumberg
ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30
 ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30 ARMA modely - motivácia I. Odhadneme ACF a PACF pre dáta a nepodobajú sa
ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30 ARMA modely - motivácia I. Odhadneme ACF a PACF pre dáta a nepodobajú sa
Vzt'ah tenzorov T ij a σ ij v mechanike tekutín Marián Fecko KTF&DF, FMFI UK, Bratislava Ciel'om je pozriet' sa vzt'ah tenzorov T ij a σ ij. Oba súvis
 zt'ah tenzorov T ij a σ ij v mechanike tekutín Marián Fecko KTF&DF, FMFI UK, Bratislava Ciel'om je pozriet' sa vzt'ah tenzorov T ij a σ ij. Oba súvisia s bilanciou hybnosti tekutiny. Táto bilancia sa dá
zt'ah tenzorov T ij a σ ij v mechanike tekutín Marián Fecko KTF&DF, FMFI UK, Bratislava Ciel'om je pozriet' sa vzt'ah tenzorov T ij a σ ij. Oba súvisia s bilanciou hybnosti tekutiny. Táto bilancia sa dá
Pokrocilé programovanie XI - Diagonalizácia matíc
 Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Experimentálna identifikácia nelineárneho dynamického systému pomocou
 Experimentálna identifikácia nelineárneho dynamického systému pomocou IDENT Tool v prostredí Matlab Jakub ČERKALA, Anna JADLOVSKÁ Katedra kybernetiky a umelej inteligencie, Fakulta elektrotechniky a informatiky,
Experimentálna identifikácia nelineárneho dynamického systému pomocou IDENT Tool v prostredí Matlab Jakub ČERKALA, Anna JADLOVSKÁ Katedra kybernetiky a umelej inteligencie, Fakulta elektrotechniky a informatiky,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VALUE-AT-RISK A CONDITIONAL VALUE-AT-RISK AKO NÁSTROJE NA MERANIE RIZIKA P
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VALUE-AT-RISK A CONDITIONAL VALUE-AT-RISK AKO NÁSTROJE NA MERANIE RIZIKA PORTFÓLIA DIPLOMOVÁ PRÁCA 2016 Bc. Michaela JA URKOVÁ
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VALUE-AT-RISK A CONDITIONAL VALUE-AT-RISK AKO NÁSTROJE NA MERANIE RIZIKA PORTFÓLIA DIPLOMOVÁ PRÁCA 2016 Bc. Michaela JA URKOVÁ
Viacrozmerné úlohy RBC-typu
 Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Viacrozmerné úlohy RBC-typu (Diplomová práca) Bc. Vladimír Balla tudijný odbor: Ekonomická a nan ná matematika Vedúci práce: Prof.
Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Viacrozmerné úlohy RBC-typu (Diplomová práca) Bc. Vladimír Balla tudijný odbor: Ekonomická a nan ná matematika Vedúci práce: Prof.
Študijný program (Študijný odbor) Školiteľ Forma štúdia Téma Požiadavky na prijatie Výzbroj a technika ozbrojených síl (8.4.3 Výzbroj a technika ozbro
 (8.4.3 ) doc. Ing. Martin Marko, CSc. e mail: martin.marko@aos.sk tel.:0960 423878 Elektromagnetická kompatibilita mobilných platforiem komunikačných systémov. Zameranie: Analýza metód a prostriedkov vedúcich
(8.4.3 ) doc. Ing. Martin Marko, CSc. e mail: martin.marko@aos.sk tel.:0960 423878 Elektromagnetická kompatibilita mobilných platforiem komunikačných systémov. Zameranie: Analýza metód a prostriedkov vedúcich
1. KOMPLEXNÉ ČÍSLA 1. Nájdite výsledok operácie v tvare x+yi, kde x, y R. a i (5 2i)(4 i) b. i(1 + i)(1 i)(1 + 2i)(1 2i) (1 7i) c. (2+3i) a+bi d
 KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia p
 4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia pre funkcie viacerých premenných je univerzálna metóda,
4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia pre funkcie viacerých premenných je univerzálna metóda,
Matematika 2 - cast: Funkcia viac premenných
 Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
Matematický model činnosti sekvenčného obvodu 7 MATEMATICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčnéh
 7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22
 Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22 Príklad 1 AR(2) proces z prednášky: x t =1.4x t 1 0.85x t 2 +u t V R-ku: korene charakteristického polynómu
Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22 Príklad 1 AR(2) proces z prednášky: x t =1.4x t 1 0.85x t 2 +u t V R-ku: korene charakteristického polynómu
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 1. 3. marca 2006 2. 10. marca 2006 c RNDr. Monika Molnárová, PhD. Obsah 1 Aritmetické vektory a matice 4 1.1 Aritmetické vektory........................
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 1. 3. marca 2006 2. 10. marca 2006 c RNDr. Monika Molnárová, PhD. Obsah 1 Aritmetické vektory a matice 4 1.1 Aritmetické vektory........................
Rozvojom spoločnosti najmä v druhej polovici minulého storočia dochádza čím ďalej tým viac k zásahu človeka do životného prostredia
 3 Prenos hmoty a energie 3.1 Stacionárny prípad 1. Prúd vody v rieke s prietokom Qs 10m 3 /s má koncentráciu chloridov cs 20mg/l. Prítok rieky s prietokom Qw 5m 3 /s má koncentráciu chloridov cw 40mg/l.
3 Prenos hmoty a energie 3.1 Stacionárny prípad 1. Prúd vody v rieke s prietokom Qs 10m 3 /s má koncentráciu chloridov cs 20mg/l. Prítok rieky s prietokom Qw 5m 3 /s má koncentráciu chloridov cw 40mg/l.
1 Portál pre odborné publikovanie ISSN Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika
 1 Portál pre odborné publikovanie ISSN 1338-0087 Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika 28.04.2010 Článok spočíva v predstavení a opísaní algoritmu
1 Portál pre odborné publikovanie ISSN 1338-0087 Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika 28.04.2010 Článok spočíva v predstavení a opísaní algoritmu
Monday 25 th February, 2013, 11:54 Rozmerová analýza M. Gintner 1.1 Rozmerová analýza ako a prečo to funguje Skúsenost nás učí, že náš svet je poznate
 Monday 25 th February, 203, :54 Rozmerová analýza M. Gintner. Rozmerová analýza ako a prečo to funguje Skúsenost nás učí, že náš svet je poznatel ný po častiach. Napriek tomu, že si to bežne neuvedomujeme,
Monday 25 th February, 203, :54 Rozmerová analýza M. Gintner. Rozmerová analýza ako a prečo to funguje Skúsenost nás učí, že náš svet je poznatel ný po častiach. Napriek tomu, že si to bežne neuvedomujeme,
448pr1.vp
 Faktor a) Pevné aerosóly (prach) 1 ) a) Práce, pri ktorých je expozícia zamestnancov vyššia ako 0,3-násobok najvyššie prípustného expozi ného limitu pre daný druh pevného aerosólu, ale neprekra uje 2.
Faktor a) Pevné aerosóly (prach) 1 ) a) Práce, pri ktorých je expozícia zamestnancov vyššia ako 0,3-násobok najvyššie prípustného expozi ného limitu pre daný druh pevného aerosólu, ale neprekra uje 2.
Microsoft Word - Zaver.pisomka_januar2010.doc
 Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Informačná a modelová podpora pre kvantifikáciu prvkov daňovej sústavy SR
 Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Snímka 1
 Fyzika - prednáška 12 Ciele 5. Fyzikálne polia 5.4 Stacionárne magnetické pole 5.5 Elektromagnetické pole Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Fyzika - prednáška 12 Ciele 5. Fyzikálne polia 5.4 Stacionárne magnetické pole 5.5 Elektromagnetické pole Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Hodnotenie výkonnosti portfóli
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Hodnotenie výkonnosti portfólia Diplomová práca imon HORÁƒEK BRATISLAVA 2010 Univerzita
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Hodnotenie výkonnosti portfólia Diplomová práca imon HORÁƒEK BRATISLAVA 2010 Univerzita
DP.pdf
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A TATISTIKY Krátkodobé efekty dôchodkových ²okov domácností DIPLOMOVÁ PRÁCA Bratislava 2011 Bc.
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A TATISTIKY Krátkodobé efekty dôchodkových ²okov domácností DIPLOMOVÁ PRÁCA Bratislava 2011 Bc.
U N I V E R Z I T A K O M E N S K É H O Fakulta matematiky, fyziky a informatiky Katedra informatiky Vybrané kapitoly z teoretickej informatiky-ii Rie
 U N I V E R Z I T A K O M E N S K É H O Fakulta matematiky, fyziky a informatiky Katedra informatiky Vybrané kapitoly z teoretickej informatiky-ii Rie²enie aºkých problémov (Pomocné texty k predná²ke 2AIN205)
U N I V E R Z I T A K O M E N S K É H O Fakulta matematiky, fyziky a informatiky Katedra informatiky Vybrané kapitoly z teoretickej informatiky-ii Rie²enie aºkých problémov (Pomocné texty k predná²ke 2AIN205)
Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x x x 1 s.t. x 1 80 x 1 + x Pre riešenie úlohy vykonáme nasledujúce kroky
 Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x 2 1 + x2 2 + 60x 1 s.t. x 1 80 x 1 + x 2 120 Pre riešenie úlohy vykonáme nasledujúce kroky: 1. Najskôr upravíme ohraničenia do tvaru a následne
Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x 2 1 + x2 2 + 60x 1 s.t. x 1 80 x 1 + x 2 120 Pre riešenie úlohy vykonáme nasledujúce kroky: 1. Najskôr upravíme ohraničenia do tvaru a následne
Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1
 Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1 A Pomocou Charpitovej metódy vyriešte rovnicu. x u x + y u y = u u x y u 2 = xy u u x y 3. u 2 y = u y u 4. u 2 x = u x u u x = B.
Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1 A Pomocou Charpitovej metódy vyriešte rovnicu. x u x + y u y = u u x y u 2 = xy u u x y 3. u 2 y = u y u 4. u 2 x = u x u u x = B.
Snímka 1
 Fyzika - prednáška 11 Ciele 5. Fyzikálne polia 5.2 Elektrostatické pole 5.3 Jednosmerný elektrický prúd Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Fyzika - prednáška 11 Ciele 5. Fyzikálne polia 5.2 Elektrostatické pole 5.3 Jednosmerný elektrický prúd Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Operačná analýza 2
 Niektoré náhodné procesy majú v praxi veľký význam, pretože sa často vyskytujú, napr.: Poissonov proces proces vzniku a zániku Wienerov proces stacionárne procesy,... Poissonov proces je homogénny Markovov
Niektoré náhodné procesy majú v praxi veľký význam, pretože sa často vyskytujú, napr.: Poissonov proces proces vzniku a zániku Wienerov proces stacionárne procesy,... Poissonov proces je homogénny Markovov
9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty 1. Systém lineárnych rovníc Systém
 9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty. Systém lineárnych rovníc Systém lineárnych rovníc, ktorý obsahuje m rovníc o n neznámych
9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty. Systém lineárnych rovníc Systém lineárnych rovníc, ktorý obsahuje m rovníc o n neznámych
Microsoft PowerPoint - Paschenov zakon [Read-Only] [Compatibility Mode]
![Microsoft PowerPoint - Paschenov zakon [Read-Only] [Compatibility Mode] Microsoft PowerPoint - Paschenov zakon [Read-Only] [Compatibility Mode]](/thumbs/101/148813443.jpg) Výboje v plynoch, V-A charakteristika Oblasť I. : U => I pri väčšej intenzite poľa (E) je pohyb nosičov náboja k elektródam rýchlejší a tak medzi ich vznikom a neutralizáciou na elektródach uplynie kratší
Výboje v plynoch, V-A charakteristika Oblasť I. : U => I pri väčšej intenzite poľa (E) je pohyb nosičov náboja k elektródam rýchlejší a tak medzi ich vznikom a neutralizáciou na elektródach uplynie kratší
60. ročník Fyzikálnej olympiády v školskom roku 2018/2019 kategória E okresné kolo Riešenie úloh 1. Zohrievanie vody, výhrevnosť paliva a) Fosílne pal
 60. ročník Fyzikálnej olympiády v školskom roku 018/019 kategória E okresné kolo Riešenie úloh 1. Zohrievanie vody, výhrevnosť paliva a) Fosílne palivá: uhlie, nafta, olej, zemný plyn. Propán-bután, lieh,
60. ročník Fyzikálnej olympiády v školskom roku 018/019 kategória E okresné kolo Riešenie úloh 1. Zohrievanie vody, výhrevnosť paliva a) Fosílne palivá: uhlie, nafta, olej, zemný plyn. Propán-bután, lieh,
Úvodná prednáška z RaL
 Rozvrhovanie a logistika Základné informácie o predmete Logistika a jej ciele Štruktúra činností výrobnej logistiky Základné skupiny úloh výrobnej logistiky Metódy používané na riešenie úloh výrobnej logistiky
Rozvrhovanie a logistika Základné informácie o predmete Logistika a jej ciele Štruktúra činností výrobnej logistiky Základné skupiny úloh výrobnej logistiky Metódy používané na riešenie úloh výrobnej logistiky
Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozos
![Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozos Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozos](/thumbs/101/150094868.jpg) Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval koval@fmph.uniba.sk 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozostávajúci z N nezávislých spinov. Každý zo spinov sa
Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval koval@fmph.uniba.sk 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozostávajúci z N nezávislých spinov. Každý zo spinov sa
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BEHAVIORÁLNE VPLYVY NA SIETE FINAN NÝCH SUBJEKTOV Diplomová práca 2013 Bc.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BEHAVIORÁLNE VPLYVY NA SIETE FINAN NÝCH SUBJEKTOV Diplomová práca 2013 Bc. Michal Mudro UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BEHAVIORÁLNE VPLYVY NA SIETE FINAN NÝCH SUBJEKTOV Diplomová práca 2013 Bc. Michal Mudro UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Testy z CSS_2015_16
 Previerkové otázky na skúšku z ČSS 1. Vyjadrite slovne a matematicky princíp superpozície pre lineárnu diskrétnu sústavu. 2. Čo fyzikálne predstavuje riešenie homogénnej a nehomogénnej lineárnej diferenčne
Previerkové otázky na skúšku z ČSS 1. Vyjadrite slovne a matematicky princíp superpozície pre lineárnu diskrétnu sústavu. 2. Čo fyzikálne predstavuje riešenie homogénnej a nehomogénnej lineárnej diferenčne
A 1
 Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Pouºitie teórie extrémnych hodnôt vo finan níctve DIPLOMOVÁ PRÁCA Bratisla
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Pouºitie teórie extrémnych hodnôt vo finan níctve DIPLOMOVÁ PRÁCA Bratislava 2008 Enik Kovácsová UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Pouºitie teórie extrémnych hodnôt vo finan níctve DIPLOMOVÁ PRÁCA Bratislava 2008 Enik Kovácsová UNIVERZITA KOMENSKÉHO V BRATISLAVE
Študijný program (Študijný odbor) Školiteľ Forma štúdia Téma Elektronické zbraňové systémy (8.4.3 Výzbroj a technika ozbrojených síl) doc. Ing. Martin
 doc. Ing. Martin Marko, CSc. e-mail: martin.marko@aos.sk tel.: 0960 423878 Metódy kódovania a modulácie v konvergentných bojových rádiových sieťach Zameranie: Dizertačná práca sa bude zaoberať modernými
doc. Ing. Martin Marko, CSc. e-mail: martin.marko@aos.sk tel.: 0960 423878 Metódy kódovania a modulácie v konvergentných bojových rádiových sieťach Zameranie: Dizertačná práca sa bude zaoberať modernými
Operačná analýza 2
 Súradnicové sústavy a zobrazenia Súradnicové sústavy v rovine (E 2 ) 1. Karteziánska súradnicová sústava najpoužívanejšia súradnicová sústava; určená začiatkom O, kolmými osami x, y a rovnakými jednotkami
Súradnicové sústavy a zobrazenia Súradnicové sústavy v rovine (E 2 ) 1. Karteziánska súradnicová sústava najpoužívanejšia súradnicová sústava; určená začiatkom O, kolmými osami x, y a rovnakými jednotkami
Slide 1
 SÚSTAVA TRANSF. VZŤAHY Plošné, objemové element Polárna Clindrická rcos rsin rcos r sin z z ds rddr dv rddrdz rcossin Sférická r sin sin dv r sin drd d z rcos Viacrozmerné integrál vo fzike Výpočet poloh
SÚSTAVA TRANSF. VZŤAHY Plošné, objemové element Polárna Clindrická rcos rsin rcos r sin z z ds rddr dv rddrdz rcossin Sférická r sin sin dv r sin drd d z rcos Viacrozmerné integrál vo fzike Výpočet poloh
9.1 MOMENTY ZOTRVACNOSTI \(KVADRATICKÉ MOMENTY\) A DEVIACNÝ MOMENT PRIEREZU
 Učebný cieľ kapitoly Po preštudovaní tejto kapitoly by ste mali ovládať: Charakteristiku kvadratických momentov prierezových plôch. Ako je definovaný kvadraticky moment plochy k osi a k pólu. Ako je definovaný
Učebný cieľ kapitoly Po preštudovaní tejto kapitoly by ste mali ovládať: Charakteristiku kvadratických momentov prierezových plôch. Ako je definovaný kvadraticky moment plochy k osi a k pólu. Ako je definovaný
Numerické riešenie všeobecnej (klasickej) DMPK rovnice.
 Numerické riešenie všeobecnej (klasickej) DMPK rovnice. J. Brndiar, R. Derian, P. Markos 11.6.27 1 Úvod Vodivost a transfér matica DMPK vs. zovšeobecnená DMPK rovnica 2 Numerické riešenie Ciel e Predpríprava
Numerické riešenie všeobecnej (klasickej) DMPK rovnice. J. Brndiar, R. Derian, P. Markos 11.6.27 1 Úvod Vodivost a transfér matica DMPK vs. zovšeobecnená DMPK rovnica 2 Numerické riešenie Ciel e Predpríprava
Snímka 1
 Fyzika - prednáška 8 Ciele 3. Kmity 3.1 Netlmený harmonický kmitavý pohyb 3. Tlmený harmonický kmitavý pohyb Zopakujte si Výchylka netlmeného harmonického kmitavého pohybu je x = Asin (ω 0 t + φ 0 ) Mechanická
Fyzika - prednáška 8 Ciele 3. Kmity 3.1 Netlmený harmonický kmitavý pohyb 3. Tlmený harmonický kmitavý pohyb Zopakujte si Výchylka netlmeného harmonického kmitavého pohybu je x = Asin (ω 0 t + φ 0 ) Mechanická
Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. Katedra matematických metód, Fa
 Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. stefan.pesko@fri.uniza.sk Katedra matematických metód, Fakulta riadenia a informatiky, Žilinská univerzita v
Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. stefan.pesko@fri.uniza.sk Katedra matematických metód, Fakulta riadenia a informatiky, Žilinská univerzita v
Paralelné algoritmy, cast c. 2
 Paralelné algoritmy, čast č. 2 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 2 Paralelné algoritmy,
Paralelné algoritmy, čast č. 2 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 2 Paralelné algoritmy,
448pr1.vp
 Faktor a) Pevné aerosóly (prach) 1 ) a) Práce, pri ktorých je expozícia zamestnancov vyššia ako 0,3-násobok najvyššie prípustného expozi ného limitu pre daný druh pevného aerosólu, ale neprekra uje 2.
Faktor a) Pevné aerosóly (prach) 1 ) a) Práce, pri ktorých je expozícia zamestnancov vyššia ako 0,3-násobok najvyššie prípustného expozi ného limitu pre daný druh pevného aerosólu, ale neprekra uje 2.
Pocítacové modelovanie - Šírenie vln v nehomogénnom prostredí - FDTD
 Počítačové modelovanie Šírenie vĺn v nehomogénnom prostredí - FDTD Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2016/2017 Úvod Hľadáme riešenia časovo závislej parciálnej diferenciálnej
Počítačové modelovanie Šírenie vĺn v nehomogénnom prostredí - FDTD Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2016/2017 Úvod Hľadáme riešenia časovo závislej parciálnej diferenciálnej
Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava
 Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava Oceňovanie amerických opcií p. 2/17 Európske a americké typy derivátov Uvažujme put
Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava Oceňovanie amerických opcií p. 2/17 Európske a americké typy derivátov Uvažujme put
UNIVERZITA KOMENSKÉHO V BRATISLAVE fakulta matematiky, fyziky a informatiky Aproximácia cien dlhopisov v dvojfaktorových modeloch úrokových mier Diplo
 UNIVERZITA KOMENSKÉHO V BRATISLAVE fakulta matematiky, fyziky a informatiky Aproximácia cien dlhopisov v dvojfaktorových modeloch úrokových mier Diplomová práca 011 Bc. Jana Halga²ová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE fakulta matematiky, fyziky a informatiky Aproximácia cien dlhopisov v dvojfaktorových modeloch úrokových mier Diplomová práca 011 Bc. Jana Halga²ová UNIVERZITA KOMENSKÉHO
Princípy tvorby softvéru Modelovanie domény
 Princípy tvorby softvéru Robert Luko ka lukotka@dcs.fmph.uniba.sk M-255 Princípy tvorby softvéru ƒo je to doménový model? Doménový model je konceptuálny model (reprezentuje koncepty (entity) a vz ahy medzi
Princípy tvorby softvéru Robert Luko ka lukotka@dcs.fmph.uniba.sk M-255 Princípy tvorby softvéru ƒo je to doménový model? Doménový model je konceptuálny model (reprezentuje koncepty (entity) a vz ahy medzi
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁ SKÁ PRÁCE Estera Vörösová Stochastické modely pro posloupnosti nervových impuls Katedr
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁ SKÁ PRÁCE Estera Vörösová Stochastické modely pro posloupnosti nervových impuls Katedra pravd podobnosti a matematické statistiky Vedoucí
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁ SKÁ PRÁCE Estera Vörösová Stochastické modely pro posloupnosti nervových impuls Katedra pravd podobnosti a matematické statistiky Vedoucí
Analýza sociálnych sietí Geografická lokalizácia krajín EU
 Analýza sociálnych sietí Geografická lokalizácia krajín EU Ekonomická fakulta TU v Košiciach 20. februára 2009 Vzt ahy medzi krajinami - teória grafov Doterajšie riešenia 1 problém farbenia grafov (Francis
Analýza sociálnych sietí Geografická lokalizácia krajín EU Ekonomická fakulta TU v Košiciach 20. februára 2009 Vzt ahy medzi krajinami - teória grafov Doterajšie riešenia 1 problém farbenia grafov (Francis
2015_URBAN
 TECHNICKÁ UNIVERZITA V KOŠICIACH Strojnícka fakulta prof. Ing. Mária Č a r n o g u r s k á, CSc. Vysokoškolská 4 040 22 Košice O P O N E N T S K Ý P O S U D O K vedeckej a odbornej spôsobilosti vypracovaný
TECHNICKÁ UNIVERZITA V KOŠICIACH Strojnícka fakulta prof. Ing. Mária Č a r n o g u r s k á, CSc. Vysokoškolská 4 040 22 Košice O P O N E N T S K Ý P O S U D O K vedeckej a odbornej spôsobilosti vypracovaný
Relačné a logické bázy dát
 Unifikácia riešenie rovníc v algebre termov Ján Šturc Zima, 2010 Termy a substitúcie Definícia (term): 1. Nech t 0,..., t n -1 sú termy a f je n-árny funkčný symbol, potom aj f(t 0,..., t n -1 ) je term.
Unifikácia riešenie rovníc v algebre termov Ján Šturc Zima, 2010 Termy a substitúcie Definícia (term): 1. Nech t 0,..., t n -1 sú termy a f je n-árny funkčný symbol, potom aj f(t 0,..., t n -1 ) je term.
17. medzinárodná vedecká konferencia Riešenie krízových situácií v špecifickom prostredí, Fakulta špeciálneho inžinierstva ŽU, Žilina, máj 2
 17. medzinárodná vedecká konferencia Riešenie krízových situácií v špecifickom prostredí, Fakulta špeciálneho inžinierstva ŽU, Žilina, 30. - 31. máj 2012 ZÁSOBOVANIE VRTUĽNÍKOV VYUŽÍVANÝCH PRI RIEŠENÍ
17. medzinárodná vedecká konferencia Riešenie krízových situácií v špecifickom prostredí, Fakulta špeciálneho inžinierstva ŽU, Žilina, 30. - 31. máj 2012 ZÁSOBOVANIE VRTUĽNÍKOV VYUŽÍVANÝCH PRI RIEŠENÍ
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1.2 Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru
 8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
FYZIKA I Rámcove otázky 1998
 Otázky k teoretickej skúške z predmetu Fyzika, ZS 2014/2015 Rámcové otázky: 1. Odvodiť vzťahy pre dráhu, rýchlosť a zrýchlenie pohybu hmotného bodu po priamke,(rovnomerný a rovnomerne zrýchlený pohyb).
Otázky k teoretickej skúške z predmetu Fyzika, ZS 2014/2015 Rámcové otázky: 1. Odvodiť vzťahy pre dráhu, rýchlosť a zrýchlenie pohybu hmotného bodu po priamke,(rovnomerný a rovnomerne zrýchlený pohyb).
Pokrocilé programovanie II - Nelineárne iteracné schémy, chaos, fraktály
 Pokročilé programovanie II Nelineárne iteračné schémy, chaos, fraktály Peter Markoš Katedra experimentálnej fyziky F2-253 Letný semester 27/28 Obsah Logistická mapa - May Period doubling, podivný atraktor,
Pokročilé programovanie II Nelineárne iteračné schémy, chaos, fraktály Peter Markoš Katedra experimentálnej fyziky F2-253 Letný semester 27/28 Obsah Logistická mapa - May Period doubling, podivný atraktor,
Microsoft Word - Zahradnikova_DP.doc
 DIPLOMOVÁ PRÁCA Priezvisko a meno: Zahradníková Dáša Rok: 2006 Názov diplomovej práce: Nepriaznivé vplyvy v elektrizačnej sústave harmonické zložky prúdu a napätia Fakulta: elektrotechnická Katedra: výkonových
DIPLOMOVÁ PRÁCA Priezvisko a meno: Zahradníková Dáša Rok: 2006 Názov diplomovej práce: Nepriaznivé vplyvy v elektrizačnej sústave harmonické zložky prúdu a napätia Fakulta: elektrotechnická Katedra: výkonových
Funkcie viac premenných
 Funkcie viac premenných January 21, 215 Regulárne zobrazenia Nech je zobrazenie X = Φ(T) dané rovnicami: x 1 = ϕ 1 (t 1, t 2,, t n), x 2 = ϕ 2 (t 1, t 2,, t n), x n = ϕ n(t 1, t 2,, t n), a ak majú funkcie
Funkcie viac premenných January 21, 215 Regulárne zobrazenia Nech je zobrazenie X = Φ(T) dané rovnicami: x 1 = ϕ 1 (t 1, t 2,, t n), x 2 = ϕ 2 (t 1, t 2,, t n), x n = ϕ n(t 1, t 2,, t n), a ak majú funkcie
Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným
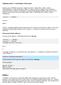 Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným dátovým typom je textový reťazec. Ako si môžeme predstaviť
Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným dátovým typom je textový reťazec. Ako si môžeme predstaviť
Preco kocka stací? - o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, ked sú velké
 o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
ZBIERKA ZÁKONOV SLOVENSKEJ REPUBLIKY Ročník 2007 Vyhlásené: Časová verzia predpisu účinná od: do: Obsah dokumentu je
 ZBIERKA ZÁKONOV SLOVENSKEJ REPUBLIKY Ročník 2007 Vyhlásené: 28. 9. 2007 Časová verzia predpisu účinná od: 1.11.2016 do: 31. 2018 Obsah dokumentu je právne záväzný. 448 VYHLÁŠKA Ministerstva zdravotníctva
ZBIERKA ZÁKONOV SLOVENSKEJ REPUBLIKY Ročník 2007 Vyhlásené: 28. 9. 2007 Časová verzia predpisu účinná od: 1.11.2016 do: 31. 2018 Obsah dokumentu je právne záväzný. 448 VYHLÁŠKA Ministerstva zdravotníctva
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UƒENIE INVARIANTNÝCH SENZO-MOTORICKÝCH REPREZENTÁCIÍ POHYBOV UCHOPOVANIA P
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UƒENIE INVARIANTNÝCH SENZO-MOTORICKÝCH REPREZENTÁCIÍ POHYBOV UCHOPOVANIA POMOCOU NEURÓNOVÝCH SIETÍ Diplomová práca 2018 Bc. Jakub
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UƒENIE INVARIANTNÝCH SENZO-MOTORICKÝCH REPREZENTÁCIÍ POHYBOV UCHOPOVANIA POMOCOU NEURÓNOVÝCH SIETÍ Diplomová práca 2018 Bc. Jakub
Light transport visualization and preturbations
 Light transport visualization and preturbations Martin Pinter Vedúci práce: Prof. RNDr. Roman Ďurikovič, PhD. FMF UK 13. júna 2014 Martin Pinter (FMF UK) Light transport visualization and preturbations
Light transport visualization and preturbations Martin Pinter Vedúci práce: Prof. RNDr. Roman Ďurikovič, PhD. FMF UK 13. júna 2014 Martin Pinter (FMF UK) Light transport visualization and preturbations
1
 1. CHARAKTERISTIKA DIGITÁLNEHO SYSTÉMU A. Charakteristika digitálneho systému Digitálny systém je dynamický systém (vo všeobecnosti) so vstupnými, v čase premennými veličinami, výstupnými premennými veličinami
1. CHARAKTERISTIKA DIGITÁLNEHO SYSTÉMU A. Charakteristika digitálneho systému Digitálny systém je dynamický systém (vo všeobecnosti) so vstupnými, v čase premennými veličinami, výstupnými premennými veličinami
Detekcia akustických udalostí v bezpečnostných aplikáciách
 TECHNICKÁ UNIVERZITA V KOŠICIACH FAKULTA ELEKTROTECHNIKY A INFORMATIKY KATEDRA ELEKTRONIKY AMULTIMEDIÁLNYCH TECHNOLÓGIÍ Metódy sledovania objektov vo videosekvenciách na báze geometrických vlastností Študijný
TECHNICKÁ UNIVERZITA V KOŠICIACH FAKULTA ELEKTROTECHNIKY A INFORMATIKY KATEDRA ELEKTRONIKY AMULTIMEDIÁLNYCH TECHNOLÓGIÍ Metódy sledovania objektov vo videosekvenciách na báze geometrických vlastností Študijný
Tue Oct 3 22:05:51 CEST Začiatky s jazykom C 2.1 Štruktúra programu Štruktúra programu by sa dala jednoducho popísať nasledovnými časťami, kto
 Tue Oct 3 22:05:51 CEST 2006 2. Začiatky s jazykom C 2.1 Štruktúra programu Štruktúra programu by sa dala jednoducho popísať nasledovnými časťami, ktoré si postupne rozoberieme: dátové typy príkazy bloky
Tue Oct 3 22:05:51 CEST 2006 2. Začiatky s jazykom C 2.1 Štruktúra programu Štruktúra programu by sa dala jednoducho popísať nasledovnými časťami, ktoré si postupne rozoberieme: dátové typy príkazy bloky
geografia.pdf
 Dopravné sektory: subregionalizácia dennej dochádzky na príklade vybraných funk ných mestských regiónov Vladimír Tóth Univerzita Komenského v Bratislave, Prírodovedecká fakulta, Katedra regionálnej geografie,
Dopravné sektory: subregionalizácia dennej dochádzky na príklade vybraných funk ných mestských regiónov Vladimír Tóth Univerzita Komenského v Bratislave, Prírodovedecká fakulta, Katedra regionálnej geografie,
Snímka 1
 HIERARCHICKÝ LINEÁRNY MODEL PRIDANEJ HODNOTY ŠKOLY VO VZDELÁVANÍ Trajová Jana, Mária Kolková, Pavol Kaclík, Lukáš Píš 20.-21.10.2015, Bratislava Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je
HIERARCHICKÝ LINEÁRNY MODEL PRIDANEJ HODNOTY ŠKOLY VO VZDELÁVANÍ Trajová Jana, Mária Kolková, Pavol Kaclík, Lukáš Píš 20.-21.10.2015, Bratislava Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je
Štruktúra Modelu Výsledky odhadu Záver Trh práce v krajinách strednej Európy: Small Search and Matching Model Martin Železník Národná Banka Slovenska
 Trh práce v krajinách strednej Európy: Small Search and Matching Model Národná Banka Slovenska Humusoft, 06.06.2013 Obsah 1 Štruktúra Modelu Domácnosti Firmy Trh práce Nastavenie miezd Uzavretie modelu
Trh práce v krajinách strednej Európy: Small Search and Matching Model Národná Banka Slovenska Humusoft, 06.06.2013 Obsah 1 Štruktúra Modelu Domácnosti Firmy Trh práce Nastavenie miezd Uzavretie modelu
JSJA_zbornikFEI2_V2
 Aplikácia DDE a OPC komunikačných protokolov v identifikácii a riadení reálneho systému Štefan JAJČIŠIN, Anna JADLOVSKÁ Katedra kybernetiky a umelej inteligencie, FEI TU v Košiciach, Slovenská republika
Aplikácia DDE a OPC komunikačných protokolov v identifikácii a riadení reálneho systému Štefan JAJČIŠIN, Anna JADLOVSKÁ Katedra kybernetiky a umelej inteligencie, FEI TU v Košiciach, Slovenská republika
S rok 2 roky t = 4 1 rok MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku informatiku Monika Molnárová Košice 2018
 S 230 280 270 0 1 2 3 4 5 1 rok 2 roky t = 4 1 rok MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku informatiku Monika Molnárová Košice 2018 MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku
S 230 280 270 0 1 2 3 4 5 1 rok 2 roky t = 4 1 rok MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku informatiku Monika Molnárová Košice 2018 MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku
Regulované napájacie zdroje DC AX-3005DBL jednokanálový AX-3005DBL 3-trojkanálový
 Regulované napájacie zdroje DC AX-3005DBL jednokanálový AX-3005DBL 3-trojkanálový Návod na obsluhu Kapitola 1. Inštalácia a odporúčania týkajúce sa používania Počas inštalácie napájacieho zdroja bezpodmienečne
Regulované napájacie zdroje DC AX-3005DBL jednokanálový AX-3005DBL 3-trojkanálový Návod na obsluhu Kapitola 1. Inštalácia a odporúčania týkajúce sa používania Počas inštalácie napájacieho zdroja bezpodmienečne
Hospodarska_informatika_2015_2016a
 Gestorská katedra: Študijný program 1. stupňa: Garant študijného programu: KAI FHI EU v Bratislave Hospodárska informatika denné štúdium 1. ročník doc. Ing. Gabriela Kristová, PhD. Bakalárske štúdium -
Gestorská katedra: Študijný program 1. stupňa: Garant študijného programu: KAI FHI EU v Bratislave Hospodárska informatika denné štúdium 1. ročník doc. Ing. Gabriela Kristová, PhD. Bakalárske štúdium -
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE PRÍJMOV A VÝDAVKOV NA ZDRAVOTNÚ STAROSTLIVOS Diplomová práca B
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE PRÍJMOV A VÝDAVKOV NA ZDRAVOTNÚ STAROSTLIVOS Diplomová práca Bratislava, 2011 Bc. Jana a ová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE PRÍJMOV A VÝDAVKOV NA ZDRAVOTNÚ STAROSTLIVOS Diplomová práca Bratislava, 2011 Bc. Jana a ová UNIVERZITA KOMENSKÉHO
