UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA A NÁVRH NUMERICKÝCH ALGORITMOV NA RIE ENIE NELINEÁRNYCH ROVNÍC BLA
|
|
|
- Magdalena Přibylová
- pred 4 rokmi
- Prehliadani:
Prepis
1 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA A NÁVRH NUMERICKÝCH ALGORITMOV NA RIE ENIE NELINEÁRNYCH ROVNÍC BLACK - SCHOLESOVHO TYPU DIPLOMOVÁ PRÁCA 2012 Bc. Jana Sekerová
2 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZYKY A INFORMATIKY ANALÝZA A NÁVRH NUMERICKÝCH ALGORITMOV NA RIE ENIE NELINEÁRNYCH ROVNÍC BLACK - SCHOLESOVHO TYPU DIPLOMOVÁ PRÁCA tudijný program: Ekonomická a nan ná matematika tudijný odbor: Aplikovaná matematika 1114 koliace pracovisko: Vedúci práce: Katedra aplikovanej matematiky a ²tatistiky prof. RNDr. Daniel EVƒOVIƒ, CSc. Bratislava 2012 Bc. Jana SEKEROVÁ
3
4 Po akovanie Touto cestou sa chcem po akovat svojmu vedúcemu diplomovej práce prof. RNDr. Danielovi ev ovi ovi, CSc. za ochotu, pomoc, odborné rady a podnetné pripomienky, ktoré mi pomohli pri písaní tejto práce.
5 ƒestné vyhlásenie len s pouºsitím uvedenej odbornej literatúry. Vyhlasujem, ºe som diplomovú prácu vypracovala samostatne Bratislava Bc. Jana SEKEROVÁ
6 Abstrakt SEKEROVÁ, Jana: Analýza a návrh numerických algoritmov na rie²enie nelineárnych rovníc Black - Scholesovho typu [Diplomová práca], Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky, Katedra aplikovanej matematiky a ²tatistiky; ²kolite : prof. RNDr Daniel ev ovi, CSc., Bratislava, 2012, 66 strán V na²ej práci sa zaoberáme analýzou nelineárnych modelov Black - Scholesovho typu a návrhom ich numerického rie²enia. Modely ktorým sa venujeme, slúºia na ocene ovanie nan ných derivátov Európskeho typu. Ich hodnota závisí od ceny podkladového aktíva a asu do expirácie. Zameriavame sa na riziko zahr ujúcu metodológiu a model nelikvidného trhu. V oboch modeloch volatilita závisí okrem iného aj od ceny podkladového aktíva. Výhoda nelineárnych modelov je, ºe nám umoº ujú modelovanie spätnej väzby dominantného investora pri kúpe alebo predaji opcií, alebo zahrnú transak né náklady a moºné straty z nechráneného portfólia. Na ur enie hodnoty aktuálnej ceny nan ného derivátu neexistuje v²eobecný explicitný vzorec a preto pri h adaní rie²enia vyuºívame numerické schémy. Existuje nieko ko explicitných vzorcov, ktoré vyhovujú jednotlivým nelineárnym modelom, ale nedajú sa vyuºi pri reálnom oce ovaní derivátov. Tieto explicitné rie²enia nám v práci slúºia na ur enie presnosti numerického výsledku navrhnutého algoritmu. K ú ové slová: nan né deriváty, hedºovanie portfólia, Black - Scholesova rovnica, RAPM model, model nelikvidného trhu, Gama rovnica,
7 Abstract SEKEROVÁ, Jana: Analysis and numeric algorithm design for solving nonlinear Black - Scholes equations. [Master Thesis], Comenius University in Bratislava, Faculty of Mathematics, Physics and Informatics, Department of Applied Mathematics and Statistics; Supervisor: prof. RNDr Daniel ev ovi, CSc., Bratislava, 2012, 66p. In our work we investigate non-linear Black - Scholes equations and introduce numeric algorithm. We concern in models which serves to price nancial derivatives of European type. Its value depends on the price of the underlying asset and the time to expiration. We focus on the risk - adjusted pricing methodology and illiquid market model. In both models volatility depends i.a. on price of the underlying asset. Advantages of non-linear models are, that they enable us to model back-coupling, when dominant investor buys or sells options, or include transaction costs and possible loss of non-protected portfolio. There is no general explicit solution to enumerate actual price of nancial derivative, that's why we use numerical schemes to obtain it. Nevertheless there exist a couple of explicit equations which satisfy those non-linear models but they are unable to use in real pricing. These explicit solutions serves us in our work to nd accuracy of algorithm design of numerical solution. Keywords: nancial derivatives, portfolio hedging, Black - Scholes equation, RAPM model, Illiquid market model, Gamma equation
8 OBSAH Obsah Úvod 9 1 Základný poh ad do problematiky nan ných derivátov Lineárny model Príklady nelineárnych modelov Odvodenie nelineárnych modelov RAPM model Transformácia RAPM modelu na Gama rovnicu Model nelikvidného trhu Transformácia modelu nelikvidného trhu na Gama rovnicu Explicitné rie²enie nelineárnych modelov RAPM model bez zahrnutia dividend Zov²eobecnenie explicitného rie²enia Numerická schéma na rie²enie nelineárnych modelov Explicitná metóda Implicitná metóda Semi - implicitná metóda Numerické výsledky výpo tov RAPM model Model nelikvidného trhu Záver 53 Príloha 1 57 Príloha
9 ÚVOD Úvod V sú asnosti existuje obrovský po et nan ných nástrojov, s ktorými sa denno denne obchoduje na nan nom trhu. Medzi nimi sú aj nan né deriváty, ktorých cena závisí od ceny podkladového aktíva a ich primárny cie je poistenie portfólia vo i moºným stratám spôsobených nestabilitou trhu. Existuje viacero druhov nan ných derivátov, ale my sa v práci zaobedáme len opciami Európskeho typu. Hlavnú my²lienku a model oce ovania nan ných derivátov priniesli Black a Scholes, ktorí vytvorili lineárnu parciálnu diferenciálnu rovnicu, známu ako Black - Scholesova rovnica. Ich model je základom v²etkých al²ích nelineárnych modelov ktoré boli neskôr odvodené. Nelineárne modely vo v²eobecnosti nemajú explicitné rie²enie a preto sa na nájdenie rie²enia vyuºívajú numerické schémy. Hoci je výpo et pomocov týchto modelov zna ne zloºitej²í, rie²ia niektoré nedostatky a obmedzenia základného modelu. Na za iatku priblíºime problematiku nan ných nástrojov, matematické odvodenie stochastických procesov a základný lineárny model. alej sa podrobne venujeme dvom nelineárnym modelom - riziko zahr ujúcej metodológie a modelu neúplného trhu. Na základe numerických poznatkov sa snaºíme navrhnú efektívne algoritmy, ktoré nám dané modely rie²ia. Numerické výsledky algoritmov porovnáme s explitnými rie²eniami, ktoré síce vyhovujú jednotlivým modelom, pre reálne oce ovanie v²ak majú diskutabilný charakter. V aka tomu môºeme zhodnoti presnos a efektívnos navrhovanej metódy rie²enia. 9
10 1 Základný poh ad do problematiky nan ných derivátov Rozvoj nan ného trhu v posledných desa ro iach priná²a mnoho moºností pri investovaní a obchodovaní s nan nými nástrojmi. Na trhu sa stretneme s mnohými aktívami, ako sú napríklad akcie a dlhopisy. Akcia je cenný papier, ktorý umoºnuje jeho majite- ovi podiela sa na majetku príslu²nej akciovej spolo nosti, jej riadení a zisku. Cena sa denno denne mení v závislosti od dopytu a ponuky. Ponuka nan ého aktíva na predaj (ask price) je vºdy vy²²ia ako ponuka na kúpu (bid price) pri om trhová cena je výsledkom h adania rovnováhy medzi týmito ponukami. Ak sa spolo nos rozvíja a vytvára zisk, je po nej vy²²í dopyt a cena akcií rastie. Niektoré akcie môºu priná²a pravidelný výnos svojim majite om vo forme dividend, ktorých vý²ka závisí od hospodárenia spolo nosti za uplynulé obdobie. Pri zlom hospodárení a vytvorenej pe aºnej strate nemá akcionár nárok na vyplatenie divided. Akcie sú beºne obchodovate né na burzách cenných papierov, ako napríklad New Yorkská burza cenných papierov (NYSE), burza v tuttgarte (STU), vo Viedni (Wiener Börse AG) a mnohé al²ie. Kedºe ceny sa neustále menia v závislosti od pôsobenia burzového a mimoburzového trhu, dopytu a ponuky, ich asový vývoj sa nedá predpoveda. V matematickom ponímaní hovoríme, ºe má stochastický (náhodný) charakter. Z dlhodobého h adiska má vývoj cien akcií rastúci trend alebo klesajúci. Z krákodobého h adiska zvy ajne výrazne uktuujú, ako môºeme vidie na obrázku 1.1, ktorý zobrazuje pohyby cien akcií spolo nosti Google za obdobie jedného roka. Pod a výkyvov cien rozde ujeme akcie na rizikové, pri om kompenzáciou za podstúpené riziko môºe by vysoký zisk ale taktieº moºnos straty je vysoká. Menej rizikové sú také, ktorých cena je stabilnej²ia a preto sa zisk sa dosiahne s vä ²ou pravdepodobnos ou. Takéto akcie nepriná²ajú vysoký výnos. Za bezpe né nan né aktíva sa povaºujú dlhopisy, ktoré sa dajú chápa ako pôºi ka s presne stanoveným ro ným úrokom. Za bezrizikovú úrokovú mieru berieme úrok ²tátnych dlhopisov, ktoré sú brané ako bezrizikové, hoci sme v nedávnom období boli svedkami krachu Islandského ²tátu (rok 2008) a nie moc priaznivej situácie v Grécku, panielsku, i Taliansku (roky ). Na trhu sa okrem iného obchoduje aj s burzovými indexami alebo úrokovými mierami. 10
11 Akcie google Cena Google as Obr. 1.1: ƒasový vývoj ceny akcií spolo nosti Google Rozvojom nan ného trhu vznikla potreba ochrany investovaných pe azí. Snaha o elimináciu straty z investovaných pe azí do nan ných aktív sa nazýva hedºing. Finan né deriváty predstavujú ur itý druh poistky vo i poklesu, nárastu, alebo nezmenenej ceny akcii. Základným a najjednoduch²ím derivátom je forward, ktorý je zárove aj historicky prvým. Je to právo a sú astne povinnos realizácie obchodu medzi vypisovate om a kupujúcim na kúpu, respektíve predaj aktíva v presne stanovenom ase za vopred dohodnutú expira nú cenu. Ak predpokladáme, ºe cena aktíva je v ase expirácie T rovná F, sú asná cena forwardu (v ase t = 0) sa získa odúro ením budúcej o akávanej hodnoty F podkladového aktíva, P = F e r(t t). Obe strany musia tento obchod uskuto ni nezávisle od vývoja ceny akcie. Medzi al²ie nan né deriváty patria opcie, ktoré dávajú vlastníkovi právo, ale nie povinnos kúpi alebo preda dané aktívum, za vopred dohodnutú cenu vo vopred stanovenom expira nom ase. Ak sa jedná o práve kúpi, hovoríme o call opcii a ak o práve preda, potom o put opcii. Vlastník opcie je v takzvanej dlhej pozícii (long position), vypisovate (predajca) opcie je v krátkej pozícii (short position). Majite opcie má vo i vypisovate ovi výhodu výberu, i si opciu uplatní alebo nie a za túto výhodu si musí priplati takzvanú op nú prémiu. Drºite opcie si ju uplatní len vtedy, ak mu uplatnenie prinesie zisk. V sú asnosti existuje nieko ko druhov opcií, najjednoduch²ie z nich sú Európske (vanilla) opcie. Európsku call opciu si vlastník uplatní len vtedy, ak je 11
12 6 Výnos majitela call opcie 6 Výnos majitela put opcie 4 4 V(S,T) 2 V(S,T) S S Obr. 1.2: Ziskový diagram majite a opcie cena aktíva S v ase expirácie T vy²²ia ako dohodnutá cena E, pretoºe akciu predá za drah²ie, ako ju v aka uplnatnenej opcii kúpi. Pri put opcii má investor zisk, ak je cena aktíva S v stanovenom ase niº²ia ako dohodnutá cena E. Hodnota opcií v expira nom ase teda predstavuje vý²ku zisku, ktorú majite môºe dosiahnu v závislosti od ceny S: call opcia V c (S, T ) = max {S E, 0}, put opcia V p (S, T ) = max {E S, 0}, kde S je cena podkladového aktíva, T je dátum expirácie a E je dohodnutá expira ná cena. Celkový výplatný diagram majite a je e²te zníºený o cenu opcie, ktorá predstavuje zaplatenú op nú prémiu. Zisk, ktorý majite dosiahne v závislosti od ceny S v ase expliráciemôºeme vidie na obrázku 1.2. Predaná opcia, alebo taktieº opcia v short pozícii prinesie vypisovate ovi zisk, iba ak si ju jej drºite neuplatní. Výnos vtedy predstavuje cenu samotnej opcie, ktorú vypisovate zinkasuje jej predajom. Inými slovami, zisk vypisovate a je záporná hodnota zisku majite a, ako vidie aj na obrázku 1.3. Kombináciou kúpy a predaja opcií s rôznymi expira nými cenami vnikajú rôzne hedºovacie stratégie, i uº proti nárastu, poklesu, alebo nezmenej ceny akcie. Základnými a najjednodnoduch²ími stratégiami sú bullish spread a bearish spread. Bullish spread vznikne kúpou opcie s expira nou cenou E 1 a predajom s expira nou cenou E 2, 12
13 1.1 Lineárny model 2 Výnos vypisovatela call opcie 2 Výnos vypisovatela put opcie 0 0 V(S,T) 2 V(S,T) S S Obr. 1.3: Ziskový diagram vypisovate a opcie pri om E 1 < E 2. Pri stratégii bearish spread je kombinácia opa ná, iºe drzíme opciu s expira nou cenou E 2 a predáme s E 1, kde E 1 < E 2. Výplatný diagram v ase T pre obe stratégie sú zobrazené na obrázku 1.4 a sú nasledovné: Bullish spread V (S, T ) = max(s E 1, 0) max(s E 2, 0), E 1 < E 2, Bearish spread V (S, T ) = max(s E 1, 0) + max(s E 2, 0), E 1 < E 2. Ostatné stratégie vzniknú al²ími ubovo nými kombináciami kúpy a predaja call a put opcií. Okrem vanilla opcií poznáme aj Americké opcie, path-dependent opcie a al- ²ie. Americkú opciu si môºe vlastník uplatni hocikedy do asu expirácie, teda pre ubovo né t (0, T ). Hodnota path-dependent opcií závisí nie len od sú asnej hodnoty podkladového aktíva, ale aj od vývoja jeho historickej ceny na celom intervale t [0, T ]. Príkladom takýchto opcií sú Ázijské opcie, Bariérové opcie a Look-back opcie. V práci sa alej zaoberáme len Európskymi opciami. 1.1 Lineárny model Hodnota opcie v ase expirácie je známa, otázne zostáva, akú hodnotu má opcia pre t = 0 teda v ase jej kúpy. Cena musí by stanovená tak, aby nenastala arbitráº. Cena akcie má náhodný pohyb, ktorý dopredu nevieme presne predikova. Hovoríme, ºe cena 13
14 1.1 Lineárny model 8 Bullish spread 2 Bearish spread 6 0 V(S,T) 4 V(S,T) S S Obr. 1.4: Porovnanie stratégii bullish a bearish spread akcie sa riadi geometrickým Brownovým pohybom s parametrami µ a σ. Ke ºe pohyb ceny akcie S = S(t) je náhodný, potrebujeme vyuºi Itoovu lemu, v aka ktorej vieme ur i stochastickú diferenciálnu rovnicu opisujúcu tento náhodný vývoj. Lema 1.1 (Itoóva lema). [15] Nech f(x, t) je hladká funkcia dvoch premenných, pri om premenná x je rie²ením stochastickej diferenciálnej rovnice dx = µ(x, t)dt + σ(x, t)dw, kde W (t) je Wienerov proces. Potom prvý diferenciál funkcie f je daný vz ahom ( df = x fdx + t f + 1 ) 2 σ2 (x, t) xf 2 dt, dôsledkom oho funkcia f vyhovuje stochastickej diferenciálnej rovnici ( df = t f + x fµ(x, t) + 1 ) 2 σ2 (x, t) xf 2 dt + x fσ(x, t)dw. Wienerov proces je náhodný proces, ktorý má normálne rozdelenie s parametrami W (t) N(0, 1). Vývoj ceny akcie modelujeme pomocou stochastickej diferenciánej rovnice ds = µ(s, t)sdt + σ(s, t)sdw. (1.1) kde µ(s, t) je o akácaný výnos akcie, σ(s, t) je jej volatilita, ds je zmena ceny akcie za asový okamih dt a dw je diferenciál Wienerovho procesu. Cena opcie V (S, t) je funkcia dvoch premenných - ceny podkladového aktíva S a asu t. Na vyjadrenie diferenciálu vyuºijeme Itoóvu lemu. dv (S, t) = ( t V + S V Sµ(S, t) σ2 (S, t)s 2 SV ) dt + S V Sσ(S, t)dw. (1.2) 14
15 1.1 Lineárny model Odvodenie ceny derivátu V (S, t) spo íva v odvodení lineárnej Black - Scholesovej rovnice, pri om vyuºijeme Mertonovu my²lienku, kde máme portfólio Π pozostávajúce z Q S mnoºstva akcií vyplácajúcich dividendy, Q V opcií a bezrizikových dlhopisov vyplácajúcich dividendy ([15], str ). Π = SQ S + V Q V + B Dané portfólio chceme ma zaistené vo i moºným výkyvom cien akcií a s nulovým rastom investícii. Na zaistenie vo i výkyvom ho musíme dynamicky v ase prerozde ova, pri om vyuºijeme zdroje zo samotného portfólia. Nulové investície nám vytvárajú prvú podmienku Π = SQ S + V Q V + B = 0 (1.3) a zárove nám z toho vyplýva, ºe hodnota portfólia sa v ase nemení, preto zárove platí aj dπ = d(sq S + V Q V + B) = 0. (1.4) Prenancovanie daného portfólia nám hovorí o zmene mnoºstva Q V δ dlhopisov, o matematicky vieme vyjadtri : opcií, Q S akcií a SdQ S + V dq V + δb = 0. (1.5) Na oce ovanie bezkupónových dlhopisov vyuºívame jednoduchý vz ah B(t) = B(0)e tr kde r je bezriziková miera úro enia. Tento úrok sa zvy ajne udáva ako výnos zo ²tátnych dlhopisov, ktoré sú vo v²eobecnosti povaºované za bezpe né aktívum. Zmena db(t) = rb(t) vyjadruje úro enie dlhopisu, no nesmieme zabúda, ºe dlhopisy sú zárove moºné prostriedky na prerozde ovanie portfólia, pri om na toto prerozdelenie vyuºijeme δb dlhopisov, preto zmena pe aºného objedmu je db(t) = rb(t) + δb Derivovaním (1.4) a vyuºitím podmienky (1.5) dostaneme dπ = d(sq S + V Q V + B) = dsq S + dv Q V + rb + SdQ S + V dq V + δb (1.6) = dsq S + dv Q V + rb. Ke dlhopisy B vyjadríme za pomoci (1.3), získame vz ah dsq S + dv Q V rsq S dt rv Q V dt = 0. (1.7) 15
16 1.1 Lineárny model Po dosadení (1.1) a (1.2) do vz ahu (1.7) a denovaním = Q S Q V, kde predstavuje pomer po tu Q S akcií a po tu Q V opcií drºaných v portfóliu, dostaneme rovnicu ( t V + µ(s, t)s S V + 1 ) 2 σ2 (S, t)s 2 SV 2 µ(s, t)s + rs rv dt (1.8) ( σ(s, t)s σ(s, t)s S V ) dw = 0 Ke ºe berieme do úvahy akciu vyplácajúcu dividendy, stredná hodnota stochastického procesu je v tvare µ q. Volatilitu σ = σ(s, t) môºeme ur i rôznymi spôsobmi, jedným z nich je uvaºova pevnú volatilitu na základe historických dát, prípadne ju vypo íta implicitne. Odstránenie rizikového stochastického faktora dw zabezpe íme výberom = S V. Ak stále udrºujeme takýto pomer akcií a opcií, zabezpe íme si tým elimináciu rizika, pretoºe nám v procese vystupujú len deterministické leny dt a ºiadne stochastické dw. Pomocou tohoto pomeru vieme zisti cenu opcie V (S, t) závislú od ceny akcie S pre as t [0, T ], ktorá je rie²ením lineárnej parciálnej diferenciálnej rovnice t V + (r q)s S V + σ2 2 S2 2 SV rv = 0, (1.9) s po iato nými podmienkami V (S, T ) = max(s E, 0) pre Call opciu a V (S, T ) = max(e S, 0) pre Put opciu. V rovnici σ predstavuje volatilitu procesu, r > 0 je úroková miera bezkupónového dlhopisu, q je výnos z dividend. Pre kon²tantnú σ > 0 sa rovnica (1.9) nazýva lineárna Black-Scholesova diferenciálna rovnica. Predpokladom fungovania tohto modelu sú dos obmedzujúce poºiadavky: - úplnos trhu, - trh je dokonale likvidný, - investor môºe obchodova s ubovo ným po tom akcií bez ovplyvnenia jeho ceny, - ºiadne obmedzenia na shortselling - ºiadne transak né náklady, - dokonalá delite nos cenných papierov - lognormálne rozdelenie cien,... 16
17 1.2 Príklady nelineárnych modelov Takýto model je nerealistický. Môºeme v²ak zmeni kon²tantnú hodnotu σ > 0 na funkciu závislú od viacerých parametrov, pri om dostaneme nelineárnu parciálnu diferenciálnu rovnicu. Volatilita σ zapísaná vo v²eobecnom tvare vyzerá: σ = σ(s 2 SV, 2 S, T t). Pre Black-Scholesovu rovnicu s takouto volatilitou vieme do modelu zahrnú napríklad transak né náklady, neúplnos trhu, likviditu, alebo riziko z nestability portfólia. 1.2 Príklady nelineárnych modelov Vytvorenie modelu, ktorý by sp al predpoklady reálneho trhu je prakticky nemoºné. Kaºdý nelineárny model sa snaºí zabezpe i splnenie zvy ajne jedného alebo dvoch reálnych poºiadaviek. Funkcia volatility je pre kaºdý model rôzna, nan ný derivát kaºdého nelineárneho modelu sp a Black - Scholesovu rovnicu. Lelandov model Lelandov model [13] bol vytvorený na oce ovanie put a call opcie za prítomnosti transak ných nákladov pri kúpe a predaji opcií. Burzy si pri kaºdom obchodovaní ú tujú poplatky, preto uvaºujeme, ºe akcie sa nakupujú za cenu ask, ktorá je od skuto nej rovnováºnej ceny akcie navý²ená o transak ný poplatok, cena bid za ktorú aktívum predávame je o zníºená. Lineárny model je zaloºený na spojitom prerovnávaní portfólia, to by v²ak viedlo k nekone ným nákladom. Predpokladom Lenandovho modelu je, ºe prerozde ujeme portfólio kaºdých t asových jednotiek. Volatilita nadobúda tvar σ(s 2 2 SV, S, T t) = ˆσ 2 (1 Le sign( 2 SV )) (1.10) kde ˆσ > 0 predstavuje kon²tantnú historickú volatilitu vypo ítanú na základe dát, Le je takzvaná Lelandova kon²tanta Le = 2 π C 1 ˆσ t, (1.11) C predstavuje chybu zo zaokrúhlenia transak ných nákladov na 1$ transakcie, t.j. C = Sask S bid, t > 0 je nami ur ená frekvencia prerozde ovania portfólia. V praxi to S znamená to, ºe ím astej²ie prerozde ujeme portfólio, tým sú poplatky vy²²ie. Ak akciu vlastníme, vtedy je hodnota 2 S V > 0 a volatilia daná ako σ = ˆσ2 (1 Le sign( 2 S V )) 17
18 1.2 Príklady nelineárnych modelov je men²ia ako pri klasickom Black - Scholesovom modeli, pri om cena takéhoto nan ného derivátu je pri ostatných nezmenených parametroch niº²ia. Ak akciu nevlastníme a je v tzv. krátkej pozícii, vtedy je cena derivátu konkávna funkcia, S 2V < 0 a volatilita nadobúda vy²²iu hodnotu. RAPM model RAPM, alebo Riziko zahr ujúca metodológia je nelineárny model, ktorý vytvoril Kratka [9] a neskôr bol zov²eobecnený Janda kom a ev ovi om [11]. Tento model zah a transak né náklady podobne ako Lelandov model, no taktieº berie do úvahy rastúce riziko neprerozde ovaného portfólia. Ak uvaºujeme opciu v dlhej pozícii, potom je volatilita v tvare σ 2 = ˆσ ( µ(s SV 2 ) 1/3), (1.12) ak v krátkej, potom σ 2 = ˆσ 2 ( 1 µ(s 2 SV ) 1/3), (1.13) kde ˆσ 2 je volatilita vypo ítaná na základe historických dát, µ = 3( C2 R 2π )1/3, C predstavujú relatívne náklady na 1$ transakcie pri kúpe, alebo predaji akcií S a R koecient prémie za riziko. Tomuto modelu sa viac venujeme v al²ej kapitole. Model so skákajúcimi volatilitami Týmto modelom sa zaoberali Avellaneda a kol. [1], pri om uvaºovali s moºnos neúplnosti trhu. Volatilita nie je presne ur ená a je viazaná. ˆσ 1, 2 ak σ 2 (S 2 SV, 2 S 2 S, T t) V < 0, ˆσ 2, 2 ak S 2V > 0, σ 1, σ 2 je ur itá horná a dolná apriórna hranica, ktorá môºe by ur ená na základe historických dát. Model nelikvidného trhu Existuje aj model, ktorý sa zaoberá vplyvom ve kého investora na cenu podkladového aktíva. Tento model zov²eobecnil Frey a kol. [8] a volatilita podkladového aktívna má tvar: σ 2 = ˆσ 2 (1 ρs 2 S V )2. 18
19 1.2 Príklady nelineárnych modelov V tomto modeli vystupuje parameter ρ, ktorý je parametrom likvidity. Likvidita hovorí o tom, ako dlho trvá, kým sa podarí zameni akciu za iný tovar alebo peniaze. Peniaze sú vo v²eobecnosti dokonale likvidné, lebo výmena za tovar je moºná vºdy a okamºite. Ak je parameter ρ nulový, akcia je dokonale likvidná rovnako ako peniaze a máme lineárnu Black - Scholesovu rovnicu (1.9). Ak je ρ < 0, znamená to, ºe je po tovare vä ²í dopyt ako ponuka, akcia sa ahko predá a v aka tomu cena môºe by vy²²ia. Naopak, ak je ρ > 0, vtedy ponuka prevy²uje dopyt, cena akcie je niº²ia a je aº²ie ju preda. Model so zahrnutou preferenciou investora Model s nelineárnou volatilitou, ktorý vytvorili Barles a Soner [3], vyjadruje preferencie investora pomocou exponenciálnej funkcie uºito nosti: σ 2 (S 2 2 SV, S, T t) = ˆσ 2 (1 + Ψ(a 2 e rτ S 2 2 SV, S, τ)), kde Ψ(x) je rie²ením diferenciálnej rovnice: Ψ 1 (x) = (Ψ(x) + 1) 2, pri om Ψ(0) = 0. xψ(x) x 19
20 2 Odvodenie nelineárnych modelov Hoci je lineárny model jednoduchý na rie²enie a vieme ho explicitne rie²i, kvôli obmedzujúcim predpokladom vznikajú vo výsledkoch v porovnaní s reálnymi dátami zna né odchýlky. Preto, ako uº bolo spomenuté vy²²ie, vznikali zloºitej²ie modely, ktoré boli kvôli svojej nelinearite náro nej²ie na nájdenie rie²enia, ale zahr ujú aspo jeden reálny predpoklad navy²e. V kapitole bliº²ie predstavíme riziko zahr ujúcu metodológiu ( alej ako RAPM) a model nelikvidného trhu. 2.1 RAPM model RAPM model [11] je nelineárny model, ktorý zah a okrem transak ných nákladov vzniknutých pri kúpe a predaji podkladového aktíva, aj riziko spojené s nechráneným portfóliom. ƒím astej²ie sa portfólio prerozde uje, tým sú celkové náklady vy²²ie a naopak, ím menej sa portfólio prerozde uje, tým sa stáva portfólio nechránené, volatilita portfólia je vy²²ia a stáva sa rizikovej²ím. Cie om modelu je nájdenie optimálnej frekvencie prerozde ovania portólia tak, aby sa minimalizovali celkové straty z moºného rizika alebo prerozde ovania. Odvodenie modelu je zaloºené na nasledovných predokladoch. 1. Uvaºujme portfólio zloºené z jednej opcie a delta prislúchajúcich akcií Π = V +δs, pri om prerozde ujeme kaºdých t asových jednotiek. 2. Cena akcie opisuje geometrický Brownov pohyb v diskrétnej forme S = µs t+ σsφ t, a Φ je náhodná premenná z N(0, 1). 3. Opcia je v dlhej pozícií, iºe akciu vlastníme. 4. Transak né náklady sú dané relatívne k cene akcie. Akciu kupujeme za drah²iu cenu S ask = S(1 + C ) a predávame za lacnej²iu S 2 bid = S(1 C ), pri om S = 2 S ask +S bid 2. Uvaºujeme samonancovaciu stratégiu, takºe prostriedky, ktoré chceme vyuºi na kúpu (predaj) opcií, musíme vykry z predaja (kúpy) akcií. Zmena portfólia v ase vyjadruje rozdiel medzi novou hodnotou po prerozdelení a pôvodnou hodnotou Π = Π(t+ t) Π(t). V portfóliu chceme prerozde ovaním minimalizova riziko. Ak je riziko portfólia 20
21 2.1 RAPM model nulové, na to aby nevznikla arbitráº, hodnota portfólia by mala v ase rás rovnakou úrokovou mierou r ako bezrizikové portfólio, Π = rπ t. Akcie sa za bezrizikové nepovaºujú, preto ºiadame za podstúpenie rizika pri investovaní vy²²í výnos. Rozdiel výnosu rizikovej akcie oproti výnosu bezrizikových aktív je prémia za riziko a je tým vy²²ia, ím sú akcie rizikovej²ie. Ako uº bolo vy²²ie spomenuté, daná odmena za riziko je kompenzáciou za transak né náklady a volatilnos portfólia, preto si investor za podstúpenie oboch rizík výnos vo vý²ke r R = r T C + r V P. Ke ºe vo v²eobecnosti môºu akcie vypláca dividendy vo vý²ke qs, celková zmena hodnoty ná²ho portfólia za as t je vyjadrená nasledovne: Π = rπ t δqs t + r R S t (2.1) Ako uvádzajú Janda ka so ev ovi om v [11], na získanie jednotlivých rizík môºeme uvaºova dve samostatné úlohy. Najskôr chví u uvaºujeme nulové straty z volatility portfólia r V P = 0. Chceme prerozdeli portfólio predaním alebo kúpou akcií. Za as t sú asne dochádza k zmene hodnôt opcie a akcie. Celková zmena hodnoty portfólia predstavuje zmenu hodnoty opcie ktorú drºíme, zmenu hodnoty delta drºaných akcií δ S a to celé je e²te zníºené o náklady vynaloºené na prerozdelenie portfólia. Kúpa jednej akcie predstavuje náklady vo vý²ke S C, pre celkovú zmenu δ po tu akcií to je 2 S C 2 δ. Zmenu hodnoty portfólia Π matematicky vyjadríme ako Π = V + δ S S C 2 δ, (2.2) kde C S predstavuje stratu, ktorá vzniká pri kúpe a predaji jednej akcie. Ak na na²e 2 portfólio aplikujeme Itoóvu lemu a spojíme vz ahy (2.1) a (2.2), dostaneme ( t V σ2 S 2 2 SV ) t + ( S V + δ) S S C 2 δ = (rπ δqs r T CS) t. (2.3) Podobne ako v kapitole 1.1 chceme minimalizova straty odstránením stochastických lenov v rovnici. Kedºe ds má náhodný charakter kvôli stochastickému lenu dw, denovaním po tu drºaných akcíí δ = S V tento náhodný len eliminujeme a dostaneme vz ah ( t V σ2 S 2 2 SV ) t S C 2 δ = (r(v S SV ) + S V qs r T C S) t. (2.4) 21
22 2.1 RAPM model Aplikovaním Itoóvej lemy na δ a zanedbaním t a lenov vy²sích rádov získame aproximáciu δ σs S 2 V W. O akávaná hodnota stochastického lena W potom je E[ W ] = 2 π t. Z kapitoly 1.1 vieme, ºe rovnica ( t V σ2 S 2 2 S V ) t r(v SV ) t + S V qs t = 0 je Black - Scholesova rovnica bez transak ných nákladov. Zahrnutím transak ných nákladov do vz ahu (1.9) nám pribudli leny S C 2 δ a r T CS t. Následným vyuºitím aproximácie pre δ získavame ur enie vý²ky odmeny r T C nakladov: r T C = CσS 2π 2 SV za riziko z transak ných 1 t. (2.5) Nie je náhoda, ºe náklady vy²li totoºné ako sú uvedené v Lelandovom modeli, pretoºe model RAPM vychádza pri odvodení práve z my²lienky tohoto modelu. Druhá úloha pozostáva v nájdení odmeny r V P za riziko nechráneného portfólia, pri om tentokrát zanedbáme transak né náklady. ƒím je volatilita porfólia vy²²ia, tým si investor ºiada vy²²iu nan nú odmenu ako kompenzáciu za vy²²ie riziko. Mieru tohto rizika je vhodné mera ako varianciu zmeny hodnoty portfólia pripadajúci na hodnotu akcie za asový interval t: Π var( S r V P = R ), (2.6) t kde kon²tanta R reprezentuje krajnú hodnotu, kedy je e²te investor ochotný vystavi sa riziku. Inak povedané je to koecient prémie za riziko. Aplikovaním Itoóvej lemy na Π = V + δ S dostaneme Π = ( S V + δ)σs W σ2 S 2 2 SV ( W ) 2 + G (2.7) kde G = ( S V + δ)µs t + t V t. Kedºe G obsahuje len deterministické leny, platí E(G) = G. Vieme, ºe W predstavuje Wienerov proces v diskrétnej forme, pri om W = Φ t a Φ je náhodná premenná z normálneho rozdelenia s parametrami N(0, 1), preto platí E[ W ] = 0 a E[ W ] 2 = 1. Nás zaujíma hodnota variancie var( Π) = E[( Π E( Π)) 2 ], preto najskôr vypo ítame Π E[ Π]: Π E[ Π] = ( S V + δ)σsφ t σ2 S 2 2 SV (Φ 2 1) t. (2.8) 22
23 2.1 RAPM model Pri odvodzovaní transak ných nákladov sme stanovili podmienku δ = S V. Zo ²tatistiky platí E[(Φ 2 1) 2 ] = 2. Variancia zmeny hodnoty portfólia je preto rovná: var( Π) = E[( Π E( Π)) 2 ] = E[(( S V + δ)σsφ t σ2 S 2 2 SV (Φ 2 1)) 2 ] (2.9) = E[ 1 2 σ4 S 4 ( 2 SV ) 4 t 2 ]. Pre zjednodu²enie zápisu si denujme Γ = S 2 V. S vyuºitím (2.6) a (2.9) dostaneme r V P = 1 2 Rσ4 S 2 Γ 2 t. (2.10) Získali sme vyjadrenie pre prémie za obe riziká; riziko z transak ných nákladov r T C a riziko z volatility portfólia r V P. Uvaºujme, ºe investor je rizikovo averzný a preto sa snaºíme dané riziko minimalizova. H adáme minimum nasledovnej r R ( t) funkcie: r R = r T C + r V P = CσS 2π Γ 1 t Rσ4 S 2 Γ 2 t. (2.11) Minimum nájdeme derivovaním (2.11) pod a t a výsledok poloºíme rovný nule: 0 = CσS 2π Γ 1 ( t) 2/ Rσ4 S 2 Γ 2. (2.12) Minimálnu hodnotu celkového rizika dosiahneme stanovením optimálnej frekvencie t opt prerozdelenia: pri om K = ( C R t opt = K 2, (2.13) σ 2 SΓ 2/3 1 2π ) 1/3. Spätným dosadením (2.13) do (2.11) získame r R ( t opt ) = 3 2 ( ) C 2 (1/3) R σ 2 SΓ 4/3. (2.14) 2π Týmto sme dostali vyjadrenie optimálnej frekvencie prerozdelenia portfólia a zárove o akávanú hodnotu prémie za riziko. Zo vzorca (2.11) vidie, ako sme aj v úvode kapitoly spomínali, ºe pre t 0,, r T C teda rastú náklady z prerozdelenia portfólia a pre t r V P, teda zniºovaním frekvencie prerozde ovania zvy²ujeme rizikovos portfólia a tým moºné straty. Teraz nám ostáva uº len odvodi parciálnu diferenciálnu rovnicu, ktorá vyhovuje RAPM modelu. Vychádzame z rovnice (2.1). Po aplikovaní Itoóvej lemy a stanovením podmienky δ = S V dostaneme: t V + σ2 2 S2 2 SV + (r q)s S V rv + r R S = 0. (2.15) 23
24 2.1 RAPM model Po dosadení (2.14) do (2.15) a následnou úpravou dostaneme nelineárnu Black - Scholesovu parciálnu diferenciálnu rovnicu t V + σ2 2 S2 Γ(1 + µ(sγ) 1/3 ) + (r q)s S V rv = 0, (2.16) ( ) kde Γ = S 2V, µ = 3 C 2 R 1/3, 2π r je bezriziková miera bezkupónového dlhopisu a q je dividendova sadzba. Na zabezpe enie jednozna ného rie²enia je dôleºité, aby bola splnená podmienka β (H) 0. Tá je zaru ená, ak SΓ ( 3/4 µ) 3. (2.17) Janda ka a ev ovi [11, strana 242] sa tieº venovali analýze správania sa ceny opcie V = V (S, t) v ase blízkej do expirácie T. Ak denujeme τ = T t, tak za as blízky do expirácie povaºujeme τ > 0, pri om τ je malé. Lelandov model predpokladá, ºe frekvencia prerozde ovania je ove a men²ia ako τ [12,13]. Na to, aby bolo zaru ené t opt τ, sta í prida podmienku, ºe sa portfólio prerozde uje v ase blízko expirácie T. Tým pádom sme dostali dva intervaly; interval (0, t ), kde sa portfólio nemôºe prerozde ova a (t, T ), kde sa prerozde ova môºe. Na intervale kde neprerozde ujeme sú transak né náklady nulové, preto µ = 0 a platí lineárna Black - Scholesova rovnica (1.9). Danú lineárnu rovnicu vieme explicitne rie²i (pozri [15], strany 47-57), pri om hodnota opcie pre as t je daná V (S, t ) c = SN(d 1 )e q(t t ) EN(d 2 )e r(t t ), V (S, t ) p = EN( d 2 )e r(t t ) SN( d 1 )e q(t t ), kde N(d) je kumulatívna distribu ná funkcia, d 1 = ln(s/e) + (r q + σ2 /2)(T t ) σ T t, d 2 = d 1 σ T t, (2.18) (2.19) pri om S je cena akcie, E je expira ná cena, r je bezriziková miera úro enia, q sú vyplácané dividendy, σ je variancia portfólia, T je as do expirácie a t je takzvaný switching time. V (S, t ) c je vzorec na získanie hodnoty call opcie a V (S, t ) p na vy íslenie hodnoty put opcie. Switching time môºeme stanovi ako minimálnu frekvenciu pri ktorej prerozde ujeme portfólio: T t = min S>0 t opt(s, t ). (2.20) 24
25 2.2 Transformácia RAPM modelu na Gama rovnicu Ak dostaníme hodnotu t opt, ktorú máme vyjadrenú ako (2.14) do (2.20), následnou úpravou dostaneme T t = C Rσ 2, (2.21) ƒas t berieme do úvahy len na intervale t [0, T ], a t < t < T. Vidíme, ºe T t > 0. Týmto sme získali podmienku C < Rσ 2, (2.22) ktorú musíme pri rie²ení úlohy uvaºova. Na intervale t [0, t ] rie²ime nelineárnu diferenciálnu rovnicu (2.16). Ke ºe explicitné rie²enie vo v²eobecnosti nepoznáme, musíme ju rie²i numericky. 2.2 Transformácia RAPM modelu na Gama rovnicu Predtým ako za neme samotnú nelineárnu parabolickú rovnicu (2.16) rie²i, najskôr si ju upravíme na vhodnej²í tvar. Ako prvé zavedieme substitúciu na nezávislé premenné: ( ) S x := ln, x R, τ = T t, τ (0, T ). (2.23) E Ukázalo sa, ºe je ve mi výhodné vyuºi aj transformáciu a zadenova si pomocnú funkciu Na základe daných substitúcií platí: x S = (Ee x ) x = Ee x = S, H(x, τ) = SΓ = S 2 SV (S, t), (2.24) β(h) = 1 2 σ2 H(1 + µ(h) 1/3 ). (2.25) x V (S, t) = S V (S, t) x S = S S V (S, t), 2 xv (S, t) = S S V (S, t) + S 2 2 SV (S, t) = S S V (S, t) + SH(x, t), (2.26) τ H(x, τ) = t (S 2 SV (S, t)) τt = t (S 2 SV (S, t)), Tieto vz ahy pre derivácie vyuºijeme pri odvodzovaní Gama rovnice. Rovnicu (2.16) dvakrát zderivujeme pod a premennej x. Po prvej derivácii dostávame rovnicu t (S x V ) + Sβ(H) + S x β(h) + (r q)(s S V + S 2 2 SV ) rs S V = 0, S ( t ( x V ) + β(h) + x β(h) + (r q)( S V + SH) r S V ) = 0. (2.27) 25
26 2.2 Transformácia RAPM modelu na Gama rovnicu Hodnota opcií pre ktoré je cena S podkladovéhe aktíva nulová, je taktieº nulová. Zaujímajú nás netriviálne rie²enia, preto rovnicu (2.27) môºeme danou premennou S predeli. Druhou deriváciou uº predelenej rovnice (2.27) dostaneme t (S 2 xv ) + x β(h) + 2 xβ(h) + (r q)(s 2 SV + x H) rs 2 SV = 0. (2.28) Denovali sme si H(x, τ) = S S 2 V (S, t) a po úprave dostaneme takzvanú Gama rovnicu, ktorú neskôr vyuºijeme pri numerickom výpo te: τ H(x, τ) = 2 xβ(h(x, τ)) + x β(h(x, τ)) + (r q) x H(x, τ) qh(x, τ), (2.29) kde τ (τ, T ), x R. Daná rovnica je narozdiel od nelineárnej parabolickej Black - Scholesovej rovnice (2.16) kvázilineárna parabolická rovnica a túto vieme pomerne jednoducho numericky rie²i. Pre call aj put opciu môºeme v²eobecne vyjadri po iato nú podmienku kde Ĥ(x) je Diracova delta funkcia Ĥ(x) = δ(x) v tvare H(x, 0) = Ĥ(x), x R, (2.30) H(x, 0) = Ĥ(x), x R. (2.31) Pripome me, ºe Diracova funkcia je funckia distribu ného charakteru taká, ºe δ(x x 0 )Φ(x)dx = Φ(x 0 ), δ(x)dx = 1, (2.32) pre ubovo nú hladkú funkciu Φ. Ako uº bolo v predchádzajúcej asti povedané, rie²enie h adáme na dvoch intervaloch. Najskôr rie²ime lineárnu Black - Scholesovu rovnicu na intervale τ (0, τ ) pomocou explicitného rie²enia (2.18). Na intervale τ (τ, T ) explicitné rie²enie nepoznáme, ale vieme, ºe nájdené rie²enie funkcie V (S, t) sp ajúce nelineárnu Black - Scholesovu rovnicu (2.16) vyhovuje aj odvodenej beta rovnici (2.25). Ostáva nám uº len ur i okrajové a po iato né podmienky H(, τ), H(, τ) a H(x, τ ) pri om vieme, ºe platí H(x, τ) = S S 2 V (S, t). Ke ºe na hranici switching time τ e²te platí explicitné rie²enie vyhovujúce lineárnej Black - Scholesovej rovnici (2.18), vyuºijeme to, ºe z explicitného rie²enia vieme vyjadri nasledovné parciálne derivácie: S V (S, t) = e q(t t) N(d 1 ), SV 2 (S, t) = e q(t t) N (d 1 ) S, T t 26 (2.33)
27 2.2 Transformácia RAPM modelu na Gama rovnicu kde S 0, t (t, T t ), r je výnos derivátu, q dividendova sadzba a d 1 = σ2 ln(s/e) + (r q + )(T 2 t ). T t Z tohoto ahko vidie, ºe poznáme po iato nú podmienku pre as τ : Ĥ(x) = H(x, τ ) = e qτ N (d 1 ), (2.34) T τ pri om τ > 0 je dostato ne malé. Okrajové podmienky vieme odvodi z nasledovných limitných vz ahov: H(+, τ) = H(, τ) = 0 (2.35) lim d 1 = +, S lim d 1 =, S lim N (d 1 ) = 0. S ± Ke numericky nájdeme rie²enie H(x, T ), musíme ho spätne transformova, aby sme dostali na²e h adané rie²nie V(S,0). Z denície S 2V (S, t) = 1 H(ln(S/E), τ) prvou S integráciou dostaneme S V (S, t) = = = S 1 s H(ln(S/E), T t)ds + K 1(t) 0 ln(s/e) ln(s/e) Ee x Ee x H(x, T t)dx + K 1(t) H(x, T t)dx + K 1 (t). Následnou integráciou odvodíme: ( S ) ln(s/e) V (S, t) = H(x, T t)dx ds + SK 1 (t) + K 2 (t) = = 0 ln(s/e) ( S ) H(x, T t)ds dx + SK 1 (t) + K 2 (t) Ee x max(s Ee x, 0)H(x, T t)dx + SK 1 (t) + K 2 (t), (2.36) kde K 1 (t) = S V (0, t), K 2 (t) = V (0, t) sú premenné nezávislé od S a v V (0, t) = S V (0, t) = 0. Po úprave získame vzorec pre Call opciu V (S, t) = max(s Ee x, 0)H(x, T t)dx. (2.37) 27
28 2.3 Model nelikvidného trhu Analogickým postupom vieme získa vzorec pre Put opciu V (S, t) = max(ee x S, 0)H(x, T t)dx). (2.38) Ako ukáºeme v práci neskôr, ak integrujeme na inom intervale ako [0, S], premenné K 1 (t) a K 2 (t) môºu by nenulové. Budú to také prípady, kedy S V (S, t) a S 2 V (S, t) nebudú ma rie²enie pre S = 0. Doteraz sme sa zaoberali my²lienkou, ºe opcia je v dlhej pozícii a v ase expirácie jej tvar je V (S, T ). V prípade, ºe opciu dlhujeme (teda je v krátkej pozícii), hodnota V (S, T ) v ase expirácie je opa ná k drºanej opcii V (S, T ) = V (S, T ). Pretoºe majite nadodúba zisk uplatnením opcie na úkor dlhovate a, celý proces V (S, t) je opa ný k V (S, t). Z tohto nám vyplýva, ºe v²etky derivácie sú taktieº s opa ným znamienkom a V (S, T ) vyhovuje Black- Scholesovej rovnici t V σ 2 2 SΓ(1 µ(sγ)1/3 ) (r q)s S V + r V = 0. Ke prenásobíme celú rovnicu hodnotou 1, dostávame tvar t V + σ 2 2 S2 Γ(1 µ(sγ) 1/3 ) + (r q)s S V r V = 0, (2.39) pri om V (S, t) = V (S, t) rie²i (2.39). Netreba zabudnú na podmienku parabolickosti, pretoºe rovnica (2.39) má rie²enie len vtedy, ak SΓ (3/4 µ) 3. (2.40) 2.3 Model nelikvidného trhu Na rozdiel od klasického lineárneho modelu, model ktorý odvodil Frey [8], berie do úvahy nelikvidnos na trhu. Táto nelikvidita trhu hovorí, ºe ak investor nakúpi ve ké mnoºstvo akcií, cena týchto akcií sa ur ite zmení. Pre investora je vtedy ove a náro nej²ie preda ve ké mnoºstvo akcií za trhovú cenu, pretoºe dopyt po nich môºe by malý. Predpokladáme, ºe cie om investora je replikácia derivátu dynamickou stratégou zaloºenou na dvoch adaptovaných procesoch (α t, β t ) [16]. Výraz α t (β t ) predstavuje po et rizikových podielov v portfóliu v ase t ( alej ozna ujeme len α(β)). V tomto modeli predpokladáme, ºe zmena ceny podkladového aktíva sa riadi stochastickou diferenciálnou rovnicou ds = µsdt + σsdw + ρsdα, (2.41) 28
29 2.3 Model nelikvidného trhu kde µ je stredná hodnota náhodného procesu, σ je volatilita daného procesu, 0 ρ ˆρ je parameter likvidity a W (t) predstavuje Wienerov proces. Uvaºujeme, ºe dynamická hedºovacia stratégia investora α(β) je hladká funkcia Φ(S, t), ktorá závisí od ceny podkladového aktíva S a asu t. Diferenciál ceny podkladovej akcie ds je daný implicitne (2.41), pretoºe dα znovu obsahuje diferenciál ceny ds. Postupne ukáºeme, ºe ho vieme vyjadri aj explicitne. Uvaºujme ds v tvare ds = b(s, t)sdt + v(s, t)sdw. (2.42) Z Itoóvej lemy, rovnakým postupom ako sme odvodili diferenciál dv (S, t) v (1.2) vieme odvodi, ºe diferenciál hedºovacej stratégie je v tvare ( ) dα = S ΦdS + t Φ + v2 (S, t) 2 2 SΦ dt. (2.43) Ak tento diferenciál dosadíme do (2.41), dostaneme ( ) (1 ρs S Φ) ds = b(s, t)sdt + v(s, t)sdw + ρs t Φ + v2 (S, t) 2 2 SΦ dt. (2.44) Z tohoto vieme ahko ur i strednú hodnotu a varianciu procesu ds ako v(s, t) = b(s, t) = σ 1 ρs S Φ, ( 1 µ + ρ 1 ρs S Φ ( v 2 (S, t) 2 )) SΦ 2. (2.45) Získali sme explicitné vyjadrenie pre ds v tvare ds = ( 1 µ + ρ 1 ρs S Φ ( )) v 2 (S, t) 2 S 2Φ Sdt + σ Sdw. (2.46) 1 ρs S Φ Odvodenie diferenciálu ceny opcie dv (S, t) a Black - Scholesovej rovnice pre model nelikvidného trhu je analogické, ako sme odvodili v kapitole 1.1, s tým rozdielom, ºe zamiesto µ uvaºujeme b(s, t) a namiesto volatility σ(s, t) uvaºujeme v(s, t). Cena opcie V (S, t) vyhovuje diferenciálnej rovnici t V + v2 (S, t) S SV + (r q)s S V rv = 0, (2.47) kde r je bezrizikový úrok a q výnos z dividend. Koecienty r a q zvyknú zanedba, aby sa zjednodu²il výpo et rie²enia. V práci taktieº h adáme rie²enie nelineárnej Black - 29
30 2.4 Transformácia modelu nelikvidného trhu na Gama rovnicu Scholesovej rovnice s nulovými hodnotami pre r a q. Na²a úloha na nájdenie rie²enia ceny opcie V (S, 0) sa nám zjednodu²ila, pri om V (S, t) vyhovuje diferenciálnej rovnici t V + v2 (S, t) S SV = 0, (2.48) po iato ná podmienka V (S, T ) je V c (S, T ) = max {S E, 0}, ak sa jedná o call opciu a V p (S, T ) = max {E S, 0}, ak o put opciu. Zostáva nám e²te vyjadri funkciu Φ. My²lienka spo íva v stratégii minimalizovania takzvaného "zero tracking erroru", inak povedané uhlovej chyby. Nulová odchýlka pod a [8] nastane vtedy, ak funkcia α = Φ(S, t) je denovaná ako delta ceny opcie V (S, t), ktorá rie²i nelineárnu Black-Scholesovu ronicu (2.48): a volatilita v(s, t) rie²enia V (S, t) je v tvare Φ(S, t) = S V (S, t), (2.49) v(s, t) = σ 1 ρs 2 S V. (2.50) Potom h adáme funkciu V (S, t), ktorá je rie²ením nelineárnej Black - Scholesovej rovnice σ 2 t V (1 ρs S 2V S2 SV 2 = 0, (2.51) )2 kde S > 0, t [0, T ]. Oproti lineárnemu modelu nastal rozdiel vo variancii procesu ds. Variancia v nelineárnom modeli nadobúda tvar σ 2 (1 ρs 2 S V )2, pri om v lineárnom hodnotu σ 2. Pre ρ > 0, σ 2 (1 ρs 2 S V )2 > σ 2, variancia v nelineárnom modeli vychádza vy²²ia, o negatívne ovplyvní aj cenu opcie - je drah²ia. Na trhu, kde nie je dokonalá likvidita, si musí dominantný investor priplati. 2.4 Transformácia modelu nelikvidného trhu na Gama rovnicu Ak chceme rie²i diferenciálnu rovnicu 2.51 pre model nelikvidného trhu, musíme podobne ako pre RAPM model v Kapitole 2.2 danú rovnicu transformova na Gama rovnicu. Postup je analogický. Zavedieme substitúciu na nezávislé premenné: ( ) S x := ln, x R, τ = T t, τ (0, T ). (2.52) E Vyuºijeme transformáciu V (S, t) na funkciu H(x, τ) v tvare H(x, τ) = S 2 SV (S, t), (2.53) 30
31 2.4 Transformácia modelu nelikvidného trhu na Gama rovnicu a denujeme pomocnú funkciu beta β(h) = σ2 2 H (1 ρh) 2. (2.54) Vyuºitím (2.54) a dosadením do (2.51) dostaneme diferenciálnu rovnicu t V + β(h)s = 0. (2.55) Funkcia V (S, t) je závisí od premenných S a t, pri om H(x, τ) od x a τ. Aby sme dostali Gama rovnicu, ktorá obsahuje len premenné x a τ, musíme danú rovnicu zderivova pod a premennej x. S vyuºitím vz ahov(2.26), ktoré sme odvodili v Kapitole 2.2, dostaneme t ( S V )S + x β(h)s + β(h)s = 0. (2.56) Cena opcie, ktorej podkladové aktívum má hodnotu S = 0, je taktieº nulová, pre S > 0 môºeme rovnicu (2.56) predeli S a následnou druhou deriváciou pod a x získame Gama rovnicu v tvare τ H = 2 xβ(h) + x β(h). (2.57) Dostali sme kvázilineárnu diferenciálnu rovnicu, ktorú vieme numericky rie²i. Hodnota opcie v ase expirácie je výsledkom rovnakej funkcie, ako pre RAPM model. Pretoºe V c (S, T ) = max {S E, 0} je výplatná funkcia pre call opciu a V p (S, T ) = max {E S, 0} pre put opciu, po iato ná podmienka je opä výsledkom Diracovej funkcie v tvare pri om H(x, 0) = Ĥ(x), x R., (2.58) Ĥ(x) = H(x, τ ) = e qτ N (d 1 ), (2.59) T τ kde τ > 0 je dostato ne malé íslo. Ako vidíme, pre τ = 0 by funkcia nebola spojitá, preto sme znovu museli vyuºi switching time τ. Pre okrajové hodnoty platí H(, τ) = H(, τ) = 0. Pre nájdené rie²enie H(x, T ) vieme spravi spätnú integráciu a získame rie²enie pre call opciu V (S, t) = max(s Ee x, 0)H(x, T t)dx. (2.60) 31
32 2.4 Transformácia modelu nelikvidného trhu na Gama rovnicu Analogicky, vzorec pre Put opciu má tvar V (S, t) = max(ee x S, 0)H(x, T t)dx). (2.61) 32
33 3 Explicitné rie²enie nelineárnych modelov Doteraz sme sa zaoberali rie²ením RAPM modelu implicitne pomocou numerického výpo tu. L.A. Borgadová sa zaoberala týmto modelom [6] a aj al²ími modelmi pomocou metódy geometrickej analýzy. Pouºitím tejto metódy sa dajú nájs viaceré explicitné rie²enia ktoré budú vyhovova RAPM modelu. Ako neskôr ukáºeme, prevodom na Gama rovnicu a h adaním H(x, τ) sa dajú odhali niektoré explicitné rie²enia. Hoci majú dané rie²enia diskutabilný charakter, môºu nám poslúºi pri skúmaní vlastností RAPM modelu, presnosti numerických výpo tov a testov. 3.1 RAPM model bez zahrnutia dividend Jedným z rie²ení, ktoré Bordagová [6] uvádza, je v tvare V (S, t) = k3 i r S ln S (k3 i β)ts + c 1 S + c 2 e rt, (3.1) kde c 1, c 2 R, r 0, β R, φ π/2 a k i musí by kore om rovnice k 3 i (1 µr 1 3 ki ) + 2rβ σ 2 = 0, (3.2) pri om berieme do úvahy iba reálne korene. Pod a znamienka mínus v zátvorke vieme, ºe sa jedná o model, kde je opcia v krátkej pozícii. Overíme, i dané explicitné rie²enie je naozaj rie²ením nelineárnej Black - Scholesovej rovnice (2.16) pre RAPM model bez zahrnutia dividend, ktorá je v tvare t V + rs S V + σ2 2 SΓ(1 µγ1/3 ) rv = 0. (3.3) Najskôr odvodíme jednotlivé parciálne derivácie, ktoré nám vystupujú v diferenciálnej rovnici: t V = (k 3 i β)s + c 2 re rt, S V = k3 i r ln S + k3 i r (k3 i β)t + c 1, 2 SV = k3 i r 1 S. 33
34 3.1 RAPM model bez zahrnutia dividend Ak dosadíme tieto leny do (3.3), dostaneme ( ) k (ki 3 β)s + c 2 re rt 3 + rs i r ln S + k3 i r (k3 i β)t + c 1 ( ( ) ) + σ2 k3 2 S2 i 1 k 3 1/3 ( ) 1 µ i k 3 r i r S r r S ln S (k3 i β)ts + c 1 S + c 2 e rt Po úprave naozaj dostaneme podmienku pre k i (3.1) v tvare k 3 i (1 µr 1 3 ki ) + 2rβ σ 2 = 0. = 0. (3.4) Uvedené rie²enie je naozaj rie²ením RAPM modelu. Zaujíma nás, i výsledok numerického spôsobu rie²enia je totoºný s explicitným rie²ením. Ke chceme získa rie²enie numericky, musíme rovnicu (3.3) transformova na Gama rovnicu τ H(x, τ) = 2 xβ(h(x, τ)) + x β(h(x, τ)) + r x H(x, τ), (3.5) kde H(x, τ) = S S 2, x = ln(s/e) a τ = T t. Z explicitného rie²enia (3.1) vieme ahko nájs tvar funkcie H(x, τ). Ke ºe 2 S V = k3 i r 1 S a zárove vieme, ºe H(x, τ) = S 2 S V, vidíme, ºe H je kon²tantné a teda je nezávislé od τ a ani od x: H(x, τ) = H = k3 i r. Ak funkciu H(x, τ) dosadíme do gama rovnice (3.5), dostaneme na oboch stranách nulovú hodnotu. To znamená, ºe vstupom a výstupom je tá istá kon²tanta H = k3 i r. V porovnaní s funkciou H(x, τ) z Kapitoly 2.2, daná transformácia nadobúdala nekon- ²tatný tvar, pri om platilo H(x, τ ) = eτ N (d 1 ) T τ, τ > 0, H(, τ) = H(+, τ) = 0. (3.6) Vidíme, ºe pre explicitné rie²enie, kde H = k3 i r, nulové okrajové podmienky nikdy nedosiahneme. Taktieº derivácie S V (S, t) a S 2 V (S, t) nie sú denované pre S = 0. Na to, aby bola úloha rie²ite ná, musíme bra do úvahy len nezáporné ceny akcií. Na obrázku 3.1 môºeme vidie priebeh funkcie V (S, t) pre parametre k i = 1, r = 0.1, µ = 0.1 3, β = 0, c 1 = 1, c 2 = 1. 34
35 3.2 Zov²eobecnenie explicitného rie²enia V(S,t) 20 0 V(S,t) t S S Obr. 3.1: Priebeh funkcie V(S, t) Bordagovej rie²enia Otázna e²te ostáva spätná transformácia z H(x, τ) na V (S, t). Funkciu H(x, τ) postupne zintegrujeme. Kedºe derivácie nie sú pre S = 0 denované, za oblas, na ktorej integrujeme si zvolíme interval [1, S]. S V (S, t) = S 1 1 k 3 ln(s/e) i s r ds + K ki 3 1(t) = 0 r dx + K 1(t) = ln(s/e) k3 i r + K 1(t), (3.7) kde K 1 (t) R je integra ná kon²tanta. Na získanie V (S, t) musíme spravi e²te jednu integráciu. V (S, t) = V (S, t) = S ln(s) k3 i r ds + K 1(t)S + K 2 (t), 1 ln(s/e) 0 xee x k3 i r dx + K 1(t)S + K 2 (t), V (S, t) = S (ln(s) ln(e)) k3 i r (S 1)k3 i r + K 1(t)S + K 2 (t), (3.8) pri om K 1 (t) = β + c 1 + ln(e) k3 i r rie²enia sú ekvivalentné. a K 2 (t) = k3 i r + c 2 e rt. Vidie, ºe jednotlivé metódy 3.2 Zov²eobecnenie explicitného rie²enia Skúsme sa najskôr zamyslie sa nad tým, o nám hovorí spätná integrácia z H(x, τ) na V (S, t) v predchádzajúcej asti. Integráciou nám vznikli koecienty K 1 (t) a K 2 (t), ktoré vieme vºdy ur i tak, aby numerické rie²enie vyhovovalo explicitnému rie²eniu. Nastoluje sa otázka, i je rie²enie invariantné vo i posunutiu. Dokáºeme nasledovné tvrdenie: 35
36 3.2 Zov²eobecnenie explicitného rie²enia Tvrdenie 3.1. Nech platí t V σ2 S 2 2 SV (1 µ(s 2 SV ) 1 3 ) + (r q)s S V rv = 0. (3.9) Ak V (S, t) rie²i (3.9), potom Ṽ (S, T ) = V (S, T ) + k 1 (t)s + k 2 (t) (3.10) je opä rie²enie, pri om k 1 (t) a k 2 (t) rie²ia oby ajné diferenciálne rovnice v tvare k 1 (t) = qk 1 (t), k 2 (t) = rk 2 (t). Dôkaz: Zo vz ahu (3.10) najskôr ur íme parciálne derivácie pre t Ṽ = V t + k 1 (t)s + k 2 (t), Ṽ (S, t). S Ṽ = S V + k 1 (t), (3.11) 2 SṼ = 2 SV. Po dosadení do nelineárnej Black - Scholesovej rovnice (2.16) a vyuºitím predpokladu (3.9) dostaneme: k 1 (t)s + k 2 (t) + (r q)sk 1 (t) + k 2 (t) = 0. (3.12) Zo vz ahu 3.12 získavame dve diferenciálne rovnice k 1 (t) = qk 1 (t), k 2 (t) = rk 2 (t) a teda Ṽ (S, T ) = V (S, T )+k 1(T )e q(t t) S+k 2 (T )e r(t t) taktieº rie²i nelineárnu Black - Scholesovu rovnicu (2.16). Kaºdé rie²enie nelineárnej Black - Scholesovej rovnice je invariantné vo i posunutiu. V predchádzajúcom explicitnom rie²ení RAPM modelu nebola zahrnutá miera výnosu z divident q, preto zov²eobecníme Bordagovej rie²enie (3.1) o túto mieru. Predpokladajme, ºe rie²enie existuje v tvare V (S, t) = A(t)S ln S + B(t)S + C(t), (3.13) kde A(t), B(t), C(t) sú koecienty závislé od asu t. t V = Ȧ(t)S ln S + Ḃ(t)S + Ċ(t), S V = A(t) ln S + A(t) + B(t), 2 SV = A(t) S. 36
37 3.2 Zov²eobecnenie explicitného rie²enia Získané leny dosadíme do nelineárnej Black - Scholesovej rovnice (2.16), aby sme na²li podmienky, ktoré musia premenné A(t), B(t), C(t) sp a. Dostávame vz ah Ȧ(t)S ln S + Ḃ(t)S + Ċ(t) + σ2 2 SA(t)(1 µ(a(t))1/3 ) +(r q)s(a(t) ln S + A(t) + B(t)) r(a(t)s ln S + B(t)S + C(t)) = 0. (3.14) Po úpraveme dostaneme: σ2 A(t)S ln S + Ḃ(t)S + Ċ(t) + 2 SA(t)(1 µ(a(t))1/3 ) + rsa(t) q(s(a(t) ln S + A(t) + B(t)) + rc(t) = 0. (3.15) Ak premenné A(t), B(t), C(t) sp ajú rovnicu (3.15), potom zov²eobecnené rie²enie (3.13) sp a nelineárnu Black-Scholesovu rovnicu pre RAPM model (2.16). Rovnicu (3.15) si môºeme rozdeli na tri jednoduché diferenciálne rovnice Ȧ(t) = qa(t), Ḃ(t) = qb(t ) σ2 2 A(t)(1 µ(a(t))1/3 ) (r q)a(t), Ċ(t) = rc(t). Rie²ením prvej a tretej dferenciálnej rovnice zo sústavy dostaneme A(t) = A T e q(t t), (3.16) C(t) = C T e r(t t). (3.17) Rie²enie druhej diferenciálnej rovnice je o nie o zloºitej²ie. Najskôr si dosadíme rie²enie A(t) = A T e q(t t) : Ḃ(t) = qb(t ) σ2 2 A T e q(t t) (1 µ(a T e q(t t) ) 1/3 ) (r q)a T e q(t t). Následne integráciou získame rie²enie B(t) = B T e q(t t) + σ2 2 A T e q(t t) ((T t) µ 3 q (A1/3 T )) + (T t)(r q)a T e q(t t) /3 3 σ2 µat q e 4/3q(T t). (3.18) Zov²eobecnené explicitné rie²enie RAPM modelu teda môºeme napísa v tvare: V (S, t) = A(t)S ln S + B(t)S + C(t), (3.19) 37
Základné stochastické procesy vo financiách
 Technická Univerzita v Košiciach Ekonomická fakulta 20. Január 2012 základné charakteristiky zmena hodnoty W t simulácia WIENEROV PROCES základné charakteristiky základné charakteristiky zmena hodnoty
Technická Univerzita v Košiciach Ekonomická fakulta 20. Január 2012 základné charakteristiky zmena hodnoty W t simulácia WIENEROV PROCES základné charakteristiky základné charakteristiky zmena hodnoty
Základy automatického riadenia - Prednáška 2
 Základy automatického riadenia Predná²ka 2 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita
Základy automatického riadenia Predná²ka 2 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita
Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava
 Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava Oceňovanie amerických opcií p. 2/17 Európske a americké typy derivátov Uvažujme put
Oceňovanie amerických opcií p. 1/17 Oceňovanie amerických opcií Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava Oceňovanie amerických opcií p. 2/17 Európske a americké typy derivátov Uvažujme put
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Ekonomická a nan ná matematika Asymptotické metódy oce ovania ázijských ty
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Ekonomická a nan ná matematika Asymptotické metódy oce ovania ázijských typov nan ných derivátov DIPLOMOVÁ PRÁCA Diplomant: Lenka
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Ekonomická a nan ná matematika Asymptotické metódy oce ovania ázijských typov nan ných derivátov DIPLOMOVÁ PRÁCA Diplomant: Lenka
Zadání čtvrté série
 Pomocný text Vektory V na²om pomocnom texte Vás prevedieme postupne afínnou geometriou, skalárnym sú inom dvoch vektorov, vektorovým sú inom a zmienime sa krátko o orientovanom obsahu a jeho vyuºití. Tento
Pomocný text Vektory V na²om pomocnom texte Vás prevedieme postupne afínnou geometriou, skalárnym sú inom dvoch vektorov, vektorovým sú inom a zmienime sa krátko o orientovanom obsahu a jeho vyuºití. Tento
Durica_Svabova
 Delta and Gamma parameter of the Black model of the futures option pricing Parametre delta a gamma Blackovho modelu oceňovania futures opcií Marek Ďurica, Lucia Švábová Abstract The paper deals with analysis
Delta and Gamma parameter of the Black model of the futures option pricing Parametre delta a gamma Blackovho modelu oceňovania futures opcií Marek Ďurica, Lucia Švábová Abstract The paper deals with analysis
Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x x x 1 s.t. x 1 80 x 1 + x Pre riešenie úlohy vykonáme nasledujúce kroky
 Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x 2 1 + x2 2 + 60x 1 s.t. x 1 80 x 1 + x 2 120 Pre riešenie úlohy vykonáme nasledujúce kroky: 1. Najskôr upravíme ohraničenia do tvaru a následne
Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x 2 1 + x2 2 + 60x 1 s.t. x 1 80 x 1 + x 2 120 Pre riešenie úlohy vykonáme nasledujúce kroky: 1. Najskôr upravíme ohraničenia do tvaru a následne
BRKOS
 Pomocný text Výroková logika autor: Viki Logika je nástroj, ktorý nám umoº uje matematicky uvaºova o veciach okolo nás. Dovo uje nám formalizova tvrdenia, ktoré chceme dokáza a zárove formalizova samotný
Pomocný text Výroková logika autor: Viki Logika je nástroj, ktorý nám umoº uje matematicky uvaºova o veciach okolo nás. Dovo uje nám formalizova tvrdenia, ktoré chceme dokáza a zárove formalizova samotný
PARAMETRE RHO A VEGA PRE FORWARD-START OPCIE Marek Ďurica ÚVOD Nakoľko časový vývoj cien aktív je nestály a sú možné aj prudké poklesov cien aktív, je
 PARAMETRE RHO A VEGA PRE FORWARD-START OPCIE Marek Ďurica ÚVOD Nakoľko časový vývoj cien aktív je nestály a sú možné aj prudké poklesov cien aktív, je snahou investorov minimalizovať možné straty, ktoré
PARAMETRE RHO A VEGA PRE FORWARD-START OPCIE Marek Ďurica ÚVOD Nakoľko časový vývoj cien aktív je nestály a sú možné aj prudké poklesov cien aktív, je snahou investorov minimalizovať možné straty, ktoré
UNIVERZITA KOMENSKÉHO V BRATISLAVE fakulta matematiky, fyziky a informatiky Aproximácia cien dlhopisov v dvojfaktorových modeloch úrokových mier Diplo
 UNIVERZITA KOMENSKÉHO V BRATISLAVE fakulta matematiky, fyziky a informatiky Aproximácia cien dlhopisov v dvojfaktorových modeloch úrokových mier Diplomová práca 011 Bc. Jana Halga²ová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE fakulta matematiky, fyziky a informatiky Aproximácia cien dlhopisov v dvojfaktorových modeloch úrokových mier Diplomová práca 011 Bc. Jana Halga²ová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VALUE-AT-RISK A CONDITIONAL VALUE-AT-RISK AKO NÁSTROJE NA MERANIE RIZIKA P
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VALUE-AT-RISK A CONDITIONAL VALUE-AT-RISK AKO NÁSTROJE NA MERANIE RIZIKA PORTFÓLIA DIPLOMOVÁ PRÁCA 2016 Bc. Michaela JA URKOVÁ
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VALUE-AT-RISK A CONDITIONAL VALUE-AT-RISK AKO NÁSTROJE NA MERANIE RIZIKA PORTFÓLIA DIPLOMOVÁ PRÁCA 2016 Bc. Michaela JA URKOVÁ
PROFIL INVESTORA - PRÁVNICKÁ OSOBA Klient Obchodné meno: IČO: CIF: Sídlo: Ulica: Obec: PSČ: Krajina: (ďalej tiež ako "Klient") UniCredit Bank Czech Re
 PROFIL INVESTORA - PRÁVNICKÁ OSOBA Klient Obchodné meno: IČO: CIF: Sídlo: Ulica: Obec: PSČ: Krajina: (ďalej tiež ako "Klient") UniCredit Bank Czech Republic and Slovakia, a.s., pobočka zahraničnej banky,
PROFIL INVESTORA - PRÁVNICKÁ OSOBA Klient Obchodné meno: IČO: CIF: Sídlo: Ulica: Obec: PSČ: Krajina: (ďalej tiež ako "Klient") UniCredit Bank Czech Republic and Slovakia, a.s., pobočka zahraničnej banky,
4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia p
 4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia pre funkcie viacerých premenných je univerzálna metóda,
4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia pre funkcie viacerých premenných je univerzálna metóda,
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Hodnotenie výkonnosti portfóli
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Hodnotenie výkonnosti portfólia Diplomová práca imon HORÁƒEK BRATISLAVA 2010 Univerzita
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Hodnotenie výkonnosti portfólia Diplomová práca imon HORÁƒEK BRATISLAVA 2010 Univerzita
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Podobnos slov (Diplomová práca) Martin Vl ák Vedúci: RN
 Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Podobnos slov (Diplomová práca) Martin Vl ák Vedúci: RNDr. Michal Forí²ek Phd. Bratislava, 2011 ii Martin
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Podobnos slov (Diplomová práca) Martin Vl ák Vedúci: RNDr. Michal Forí²ek Phd. Bratislava, 2011 ii Martin
A 1
 Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) Matematická analýza IV (ÚMV/MAN2d/10) RNDr. Lenka Halčinová, PhD.
 III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
PORTFÓLIO KLASIK HIGH RISK USD High risk rozložená investícia dôraz sa kladie na vysoký výnos pri vysokej volatilite ZÁKLADNÉ INFORMÁCIE OPTIMÁLNE POR
 PORTFÓLIO KLASIK HIGH RISK USD rozložená investícia dôraz sa kladie na vysoký výnos pri vysokej volatilite Referenčná mena: USD Odporúčaný investičný horizont: Päť rokov 100% 2.000 USD / jednorazovo alebo
PORTFÓLIO KLASIK HIGH RISK USD rozložená investícia dôraz sa kladie na vysoký výnos pri vysokej volatilite Referenčná mena: USD Odporúčaný investičný horizont: Päť rokov 100% 2.000 USD / jednorazovo alebo
Lorentzova sila a jej (zov²eobecnená") potenciálna energia Marián Fecko KTF&DF, FMFI UK, Bratislava Na predná²ke sme sa dozvedeli, ºe Lorentzova sila
 Lorentzova sila a jej (zov²eobecnená") potenciálna energia Marián Fecko KTF&DF, FMFI UK, Bratislava Na predná²ke sme sa dozvedeli, ºe Lorentzova sila (pôsobiaca na bodový náboj e v danom elektrickom a
Lorentzova sila a jej (zov²eobecnená") potenciálna energia Marián Fecko KTF&DF, FMFI UK, Bratislava Na predná²ke sme sa dozvedeli, ºe Lorentzova sila (pôsobiaca na bodový náboj e v danom elektrickom a
Biharmonická rovnica - ciže co spôsobí pridanie jedného laplasiánu
 iºe o spôsobí pridanie jedného laplasiánu tyc struna Obsah ƒo je to biharmonická rovnica 2 Malý výlet do teórie pruºnosti 3 Rovnice, okrajové podmienky, rie²enia 4... a kde ostala matematická fyzika? ƒo
iºe o spôsobí pridanie jedného laplasiánu tyc struna Obsah ƒo je to biharmonická rovnica 2 Malý výlet do teórie pruºnosti 3 Rovnice, okrajové podmienky, rie²enia 4... a kde ostala matematická fyzika? ƒo
U N I V E R Z I T A K O M E N S K É H O Fakulta matematiky, fyziky a informatiky Katedra informatiky Vybrané kapitoly z teoretickej informatiky-ii Rie
 U N I V E R Z I T A K O M E N S K É H O Fakulta matematiky, fyziky a informatiky Katedra informatiky Vybrané kapitoly z teoretickej informatiky-ii Rie²enie aºkých problémov (Pomocné texty k predná²ke 2AIN205)
U N I V E R Z I T A K O M E N S K É H O Fakulta matematiky, fyziky a informatiky Katedra informatiky Vybrané kapitoly z teoretickej informatiky-ii Rie²enie aºkých problémov (Pomocné texty k predná²ke 2AIN205)
Microsoft Word - 6 Výrazy a vzorce.doc
 6 téma: Výrazy a vzorce I Úlohy na úvod 1 1 Zistite definičný obor výrazu V = 4 Riešte sústavu 15 = 6a + b, = 4a c, 1 = 4a + b 16c Rozložte na súčin výrazy a) b 4 a 18, b) c 5cd 10c d +, c) 6 1 s + z 4
6 téma: Výrazy a vzorce I Úlohy na úvod 1 1 Zistite definičný obor výrazu V = 4 Riešte sústavu 15 = 6a + b, = 4a c, 1 = 4a + b 16c Rozložte na súčin výrazy a) b 4 a 18, b) c 5cd 10c d +, c) 6 1 s + z 4
DP.pdf
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A TATISTIKY Krátkodobé efekty dôchodkových ²okov domácností DIPLOMOVÁ PRÁCA Bratislava 2011 Bc.
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A TATISTIKY Krátkodobé efekty dôchodkových ²okov domácností DIPLOMOVÁ PRÁCA Bratislava 2011 Bc.
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE PRÍJMOV A VÝDAVKOV NA ZDRAVOTNÚ STAROSTLIVOS Diplomová práca B
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE PRÍJMOV A VÝDAVKOV NA ZDRAVOTNÚ STAROSTLIVOS Diplomová práca Bratislava, 2011 Bc. Jana a ová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE PRÍJMOV A VÝDAVKOV NA ZDRAVOTNÚ STAROSTLIVOS Diplomová práca Bratislava, 2011 Bc. Jana a ová UNIVERZITA KOMENSKÉHO
Informačná a modelová podpora pre kvantifikáciu prvkov daňovej sústavy SR
 Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BEHAVIORÁLNE VPLYVY NA SIETE FINAN NÝCH SUBJEKTOV Diplomová práca 2013 Bc.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BEHAVIORÁLNE VPLYVY NA SIETE FINAN NÝCH SUBJEKTOV Diplomová práca 2013 Bc. Michal Mudro UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BEHAVIORÁLNE VPLYVY NA SIETE FINAN NÝCH SUBJEKTOV Diplomová práca 2013 Bc. Michal Mudro UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Pouºitie teórie extrémnych hodnôt vo finan níctve DIPLOMOVÁ PRÁCA Bratisla
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Pouºitie teórie extrémnych hodnôt vo finan níctve DIPLOMOVÁ PRÁCA Bratislava 2008 Enik Kovácsová UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Pouºitie teórie extrémnych hodnôt vo finan níctve DIPLOMOVÁ PRÁCA Bratislava 2008 Enik Kovácsová UNIVERZITA KOMENSKÉHO V BRATISLAVE
Princípy tvorby softvéru Modelovanie domény
 Princípy tvorby softvéru Robert Luko ka lukotka@dcs.fmph.uniba.sk M-255 Princípy tvorby softvéru ƒo je to doménový model? Doménový model je konceptuálny model (reprezentuje koncepty (entity) a vz ahy medzi
Princípy tvorby softvéru Robert Luko ka lukotka@dcs.fmph.uniba.sk M-255 Princípy tvorby softvéru ƒo je to doménový model? Doménový model je konceptuálny model (reprezentuje koncepty (entity) a vz ahy medzi
Čiastka 205/2004
 Strana 4282 Zbierka zákonov č. 481/2004 Čiastka 205 481 o zvý še ní sumy za o pat ro va cie ho prí spev ku Vlá da pod a 4 ods. 4 zá ko na č. 236/1998 Z. z. o za o pat ro va com prí spev ku v zne ní zá
Strana 4282 Zbierka zákonov č. 481/2004 Čiastka 205 481 o zvý še ní sumy za o pat ro va cie ho prí spev ku Vlá da pod a 4 ods. 4 zá ko na č. 236/1998 Z. z. o za o pat ro va com prí spev ku v zne ní zá
9. Elastické vlastnosti kry²tálov Cie om tejto predná²ky je zhrnú základné poznatky z mechaniky kontinua. Úlohou je ur i, ako sa deformuje daný kus lá
 9. Elastické vlastnosti kry²tálov Cie om tejto predná²ky je zhrnú základné poznatky z mechaniky kontinua. Úlohou je ur i, ako sa deformuje daný kus látky pri zadaných mechanických pôsobeniach. Budeme predpoklada,
9. Elastické vlastnosti kry²tálov Cie om tejto predná²ky je zhrnú základné poznatky z mechaniky kontinua. Úlohou je ur i, ako sa deformuje daný kus látky pri zadaných mechanických pôsobeniach. Budeme predpoklada,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BAKALÁRSKA PRÁCA Bratislava 2011 Roman Kukumberg
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BAKALÁRSKA PRÁCA Bratislava 2011 Roman Kukumberg Proximal-gradient, metóda konvexného programovania BAKALÁRSKA PRÁCA Roman Kukumberg
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BAKALÁRSKA PRÁCA Bratislava 2011 Roman Kukumberg Proximal-gradient, metóda konvexného programovania BAKALÁRSKA PRÁCA Roman Kukumberg
Teória pravdepodobnosti Zákony velkých císel
 10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁ SKÁ PRÁCE Estera Vörösová Stochastické modely pro posloupnosti nervových impuls Katedr
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁ SKÁ PRÁCE Estera Vörösová Stochastické modely pro posloupnosti nervových impuls Katedra pravd podobnosti a matematické statistiky Vedoucí
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁ SKÁ PRÁCE Estera Vörösová Stochastické modely pro posloupnosti nervových impuls Katedra pravd podobnosti a matematické statistiky Vedoucí
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom
 2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22
 Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22 Príklad 1 AR(2) proces z prednášky: x t =1.4x t 1 0.85x t 2 +u t V R-ku: korene charakteristického polynómu
Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22 Príklad 1 AR(2) proces z prednášky: x t =1.4x t 1 0.85x t 2 +u t V R-ku: korene charakteristického polynómu
PriklSadzPop_CM_11_12_17
 Príklady k Informáciám o nákladoch a pridružených poplatkoch za investičné a vedľajšie služby poskytované vo vzťahu k derivátovým finančným nástrojom a cenným papierom na Capital Markets Tatra banky, a.s.
Príklady k Informáciám o nákladoch a pridružených poplatkoch za investičné a vedľajšie služby poskytované vo vzťahu k derivátovým finančným nástrojom a cenným papierom na Capital Markets Tatra banky, a.s.
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú in
 Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
trendy-3-1.pdf
 RECENZOVANÉ P VODNÍ V DECKÉ STAT KONVERTIBILNÉ OBLIGÁCIE A ŠPECIFIKÁ ICH HODNOCOVANIA 1 Doc. Ing. Božena Hrvo ová, CSc., Doc. Dr. Ing. Anna Polednáková Ekonomická univerzita v Bratislave, Fakulta podnikového
RECENZOVANÉ P VODNÍ V DECKÉ STAT KONVERTIBILNÉ OBLIGÁCIE A ŠPECIFIKÁ ICH HODNOCOVANIA 1 Doc. Ing. Božena Hrvo ová, CSc., Doc. Dr. Ing. Anna Polednáková Ekonomická univerzita v Bratislave, Fakulta podnikového
CDT
 EBA/GL/2016/09 04/01/2017 Usmernenia o korekciách modifikovanej durácie v prípade dlhových nástrojov podľa druhého pododseku článku 340 ods. 3 nariadenia (EÚ) 575/2013 1. Povinnosti týkajúce sa dodržiavania
EBA/GL/2016/09 04/01/2017 Usmernenia o korekciách modifikovanej durácie v prípade dlhových nástrojov podľa druhého pododseku článku 340 ods. 3 nariadenia (EÚ) 575/2013 1. Povinnosti týkajúce sa dodržiavania
Stochastické procesy Beáta Stehlíková Finančné deriváty, SvF STU, LS 2011/2012 Stochastické procesy p.1/29
 Stochastické procesy Beáta Stehlíková Finančné deriváty, SvF STU, LS 2011/2012 Stochastické procesy p.1/29 I. Wienerov proces, Brownov pohyb Stochastické procesy p.2/29 Stochastické procesy Stochastický
Stochastické procesy Beáta Stehlíková Finančné deriváty, SvF STU, LS 2011/2012 Stochastické procesy p.1/29 I. Wienerov proces, Brownov pohyb Stochastické procesy p.2/29 Stochastické procesy Stochastický
MO_pred1
 Modelovanie a optimalizácia Ľudmila Jánošíková Katedra dopravných sietí Fakulta riadenia a informatiky Žilinská univerzita, Žilina Ludmila.Janosikova@fri.uniza.sk 041/5134 220 Modelovanie a optimalizácia
Modelovanie a optimalizácia Ľudmila Jánošíková Katedra dopravných sietí Fakulta riadenia a informatiky Žilinská univerzita, Žilina Ludmila.Janosikova@fri.uniza.sk 041/5134 220 Modelovanie a optimalizácia
Office real estate fund o. p. f. - PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodáreníí správcovskej
 Office real estate fund o. p. f. - PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodáreníí správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.218
Office real estate fund o. p. f. - PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodáreníí správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.218
SRPkapitola06_v1.docx
 Štatistické riadenie procesov Regulačné diagramy na reguláciu porovnávaním 6-1 6 Regulačné diagramy na reguláciu porovnávaním Cieľ kapitoly Po preštudovaní tejto kapitoly budete vedieť: čo sú regulačné
Štatistické riadenie procesov Regulačné diagramy na reguláciu porovnávaním 6-1 6 Regulačné diagramy na reguláciu porovnávaním Cieľ kapitoly Po preštudovaní tejto kapitoly budete vedieť: čo sú regulačné
J&T SELECT zmiešaný o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoloč
 J&T SELECT zmiešaný o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 30.6.2018 J&T
J&T SELECT zmiešaný o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 30.6.2018 J&T
Vzt'ah tenzorov T ij a σ ij v mechanike tekutín Marián Fecko KTF&DF, FMFI UK, Bratislava Ciel'om je pozriet' sa vzt'ah tenzorov T ij a σ ij. Oba súvis
 zt'ah tenzorov T ij a σ ij v mechanike tekutín Marián Fecko KTF&DF, FMFI UK, Bratislava Ciel'om je pozriet' sa vzt'ah tenzorov T ij a σ ij. Oba súvisia s bilanciou hybnosti tekutiny. Táto bilancia sa dá
zt'ah tenzorov T ij a σ ij v mechanike tekutín Marián Fecko KTF&DF, FMFI UK, Bratislava Ciel'om je pozriet' sa vzt'ah tenzorov T ij a σ ij. Oba súvisia s bilanciou hybnosti tekutiny. Táto bilancia sa dá
Axióma výberu
 Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
GOLDENBURG GROUP LTD G O L D E N B U R G G R O U P L T D Siafi Street, Porto Bello BLD, 3rd Floor, Office 30 3, 3042 Limassol, Cyprus P
 GOLDENBURG GROUP LTD G O L D E N B U R G G R O U P L T D Siafi Street, Porto Bello BLD, 3rd Floor, Office 3 3, 342 Limassol, Cyprus P +357 22 837, F +357 243 76, info@fxglobal.com Reg. No: HE328474, TAX
GOLDENBURG GROUP LTD G O L D E N B U R G G R O U P L T D Siafi Street, Porto Bello BLD, 3rd Floor, Office 3 3, 342 Limassol, Cyprus P +357 22 837, F +357 243 76, info@fxglobal.com Reg. No: HE328474, TAX
Prenosový kanál a jeho kapacita
 Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Matematika 2 - cast: Funkcia viac premenných
 Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
J&T SELECT zmiešaný o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoloč
 J&T SELECT zmiešaný o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.217 J&T SELECT
J&T SELECT zmiešaný o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.217 J&T SELECT
Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. Katedra matematických metód, Fa
 Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. stefan.pesko@fri.uniza.sk Katedra matematických metód, Fakulta riadenia a informatiky, Žilinská univerzita v
Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. stefan.pesko@fri.uniza.sk Katedra matematických metód, Fakulta riadenia a informatiky, Žilinská univerzita v
Čiastka 064/2004
 Strana 1598 Zbierka zákonov č. 135/2004 Čiastka 64 135 VY HLÁŠ KA Mi nis ter stva ži vot né ho pros tre dia Slo ven skej re pub li ky z 27. februára 2004 o dekontaminácii zariadení s obsahom polychlórovaných
Strana 1598 Zbierka zákonov č. 135/2004 Čiastka 64 135 VY HLÁŠ KA Mi nis ter stva ži vot né ho pros tre dia Slo ven skej re pub li ky z 27. februára 2004 o dekontaminácii zariadení s obsahom polychlórovaných
Slide 1
 Diferenciálne rovnice Základný jazyk fyziky Motivácia Typická úloha fyziky hľadanie časových priebehov veličín, ktoré spĺňajú daný fyzikálny zákon. Určte trajektóriu telesa rt ( )???? padajúceho v gravitačnom
Diferenciálne rovnice Základný jazyk fyziky Motivácia Typická úloha fyziky hľadanie časových priebehov veličín, ktoré spĺňajú daný fyzikálny zákon. Určte trajektóriu telesa rt ( )???? padajúceho v gravitačnom
Viacrozmerné úlohy RBC-typu
 Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Viacrozmerné úlohy RBC-typu (Diplomová práca) Bc. Vladimír Balla tudijný odbor: Ekonomická a nan ná matematika Vedúci práce: Prof.
Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Viacrozmerné úlohy RBC-typu (Diplomová práca) Bc. Vladimír Balla tudijný odbor: Ekonomická a nan ná matematika Vedúci práce: Prof.
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1.2 Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru
 8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1
 Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1 Metódy riešenia úloh nelineárneho programovania využívajúce Lagrangeovu funkciu 2 Veta: Bod ˆx je optimálne riešenie úlohy (U3)
Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1 Metódy riešenia úloh nelineárneho programovania využívajúce Lagrangeovu funkciu 2 Veta: Bod ˆx je optimálne riešenie úlohy (U3)
Numerické riešenie všeobecnej (klasickej) DMPK rovnice.
 Numerické riešenie všeobecnej (klasickej) DMPK rovnice. J. Brndiar, R. Derian, P. Markos 11.6.27 1 Úvod Vodivost a transfér matica DMPK vs. zovšeobecnená DMPK rovnica 2 Numerické riešenie Ciel e Predpríprava
Numerické riešenie všeobecnej (klasickej) DMPK rovnice. J. Brndiar, R. Derian, P. Markos 11.6.27 1 Úvod Vodivost a transfér matica DMPK vs. zovšeobecnená DMPK rovnica 2 Numerické riešenie Ciel e Predpríprava
1 Portál pre odborné publikovanie ISSN Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika
 1 Portál pre odborné publikovanie ISSN 1338-0087 Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika 28.04.2010 Článok spočíva v predstavení a opísaní algoritmu
1 Portál pre odborné publikovanie ISSN 1338-0087 Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika 28.04.2010 Článok spočíva v predstavení a opísaní algoritmu
GOLDENBURG GROUP LTD G O L D E N B U R G G R O U P L T D Siafi Street, Porto Bello BLD, 3rd Floor, Office 30 3, 3042 Limassol, Cyprus P
 GOLDENBURG GROUP LTD G O L D E N B U R G G R O U P L T D Siafi Street, Porto Bello BLD, 3rd Floor, Office 30 3, 3042 Limassol, Cyprus P +357 2200 8307, F +357 2403 0076, info@fxglobal.com Reg. No: HE328474,
GOLDENBURG GROUP LTD G O L D E N B U R G G R O U P L T D Siafi Street, Porto Bello BLD, 3rd Floor, Office 30 3, 3042 Limassol, Cyprus P +357 2200 8307, F +357 2403 0076, info@fxglobal.com Reg. No: HE328474,
text k predná²ke a úlohy k cvi eniam z vybraných kapitol z matematiky mi²o demetrian 1 1 Funkcionálne rady, rovnomerná konvergencia 1.1 ƒíselné rady -
 text k predná²ke a úohy k cvi eniam z vybraných kapito z matematiky mi²o demetrian Funkcionáne rady, rovnomerná konvergencia. ƒísené rady - opakovanie denícia konvergencie íseného radu: uvaºujeme ísený
text k predná²ke a úohy k cvi eniam z vybraných kapito z matematiky mi²o demetrian Funkcionáne rady, rovnomerná konvergencia. ƒísené rady - opakovanie denícia konvergencie íseného radu: uvaºujeme ísený
Stat1_CV1 VES
 Štatistika 1 Cvičenie č. 1 Triedenie, Aritmetický priemer Príklad č. 1 Pri sledovaní výkonnosti zamestnancov sa v 20 sledovaných dňoch zistili nasledovné údaje o počte vybavených klientov počas smeny v
Štatistika 1 Cvičenie č. 1 Triedenie, Aritmetický priemer Príklad č. 1 Pri sledovaní výkonnosti zamestnancov sa v 20 sledovaných dňoch zistili nasledovné údaje o počte vybavených klientov počas smeny v
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY STRIEBORNÁ EKONOMIKA Diplomová práca Bratislava 2012 Bc. Zuzana Benkovská
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY STRIEBORNÁ EKONOMIKA Diplomová práca Bratislava 2012 Bc. Zuzana Benkovská UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY STRIEBORNÁ EKONOMIKA Diplomová práca Bratislava 2012 Bc. Zuzana Benkovská UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
Pokrocilé programovanie XI - Diagonalizácia matíc
 Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Štruktúra Modelu Výsledky odhadu Záver Trh práce v krajinách strednej Európy: Small Search and Matching Model Martin Železník Národná Banka Slovenska
 Trh práce v krajinách strednej Európy: Small Search and Matching Model Národná Banka Slovenska Humusoft, 06.06.2013 Obsah 1 Štruktúra Modelu Domácnosti Firmy Trh práce Nastavenie miezd Uzavretie modelu
Trh práce v krajinách strednej Európy: Small Search and Matching Model Národná Banka Slovenska Humusoft, 06.06.2013 Obsah 1 Štruktúra Modelu Domácnosti Firmy Trh práce Nastavenie miezd Uzavretie modelu
Experimenty s ekonomickAmi princApmi
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Mgr. Simona Miklo²ovi ová Autoreferát dizerta nej práce Experimenty s ekonomickými princípmi Vplyv informácií a nákladov na h
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Mgr. Simona Miklo²ovi ová Autoreferát dizerta nej práce Experimenty s ekonomickými princípmi Vplyv informácií a nákladov na h
Microsoft PowerPoint - Ch+ęmia 2008
 CHÉMIA 2008 LIPTOVSKÝ JÁN, Hotel SOREA Máj 17. 19. september 2008 Chemie Pharma Schweiz BEZPE NÝ MANA MENT CHEMICKÝCH LÁTOK 18. september 2008 Bezpe nos nos v chemických podnikoch z poh adu poznatkov OZCH
CHÉMIA 2008 LIPTOVSKÝ JÁN, Hotel SOREA Máj 17. 19. september 2008 Chemie Pharma Schweiz BEZPE NÝ MANA MENT CHEMICKÝCH LÁTOK 18. september 2008 Bezpe nos nos v chemických podnikoch z poh adu poznatkov OZCH
Analýza hlavných komponentov
 Value at Risk Voľba parametrov výpočtu VaR Confidence level Dĺžka časového obdobia Hodnota investícií do jednotlivých finančných nástrojov Identifikácia rizikových faktorov Spôsob zohľadnenia korelácií
Value at Risk Voľba parametrov výpočtu VaR Confidence level Dĺžka časového obdobia Hodnota investícií do jednotlivých finančných nástrojov Identifikácia rizikových faktorov Spôsob zohľadnenia korelácií
J&T BOND EUR o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s
 J&T BOND EUR o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.216 J&T BOND EUR
J&T BOND EUR o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.216 J&T BOND EUR
OBAL1-ZZ.vp
 Rodné íslo/ íslo povolenia na pobyt VZOR TYP A RO NÉ ZÚ TOVANIE poistného na verejné zdravotné poistenie ( alej len poistné ) zamestnanca za rok 2006 pod a 19 zákona. 580/2004 Z. z. o zdravotnom poistení
Rodné íslo/ íslo povolenia na pobyt VZOR TYP A RO NÉ ZÚ TOVANIE poistného na verejné zdravotné poistenie ( alej len poistné ) zamestnanca za rok 2006 pod a 19 zákona. 580/2004 Z. z. o zdravotnom poistení
0068-statnice-ekonomika-podniku pdf
 Ekonomika podniku - okruh. 9 ANALÝZA NÁKLADOV PODNIKU NA ZÁKLADE FINAN NÉHO Ú TOVNÍCTVA Náklady - pe ažné ocenenie spotreby podnikových výrobných faktorov vynaložených podnikom na jeho výkony a ostatné
Ekonomika podniku - okruh. 9 ANALÝZA NÁKLADOV PODNIKU NA ZÁKLADE FINAN NÉHO Ú TOVNÍCTVA Náklady - pe ažné ocenenie spotreby podnikových výrobných faktorov vynaložených podnikom na jeho výkony a ostatné
XXVI b 07 Navrh VZN granty spojene.pdf
 Mestská as Bratislava - Ružinov Materiál na rokovanie Miestneho zastupite stva mestskej asti Bratislava Ružinov d a 19. 3. 2014 Návrh všeobecne záväzného nariadenia mestskej asti Bratislava Ružinov...zo
Mestská as Bratislava - Ružinov Materiál na rokovanie Miestneho zastupite stva mestskej asti Bratislava Ružinov d a 19. 3. 2014 Návrh všeobecne záväzného nariadenia mestskej asti Bratislava Ružinov...zo
Polroná správa k o hospodárení s majetkom v Rastovom príspevkovom d.d.f. ING Tatry - Sympatia, d.d.s., a.s. Bratislava, august 2007
 Polroná správa k 30.6.2007 o hospodárení s majetkom v Rastovom príspevkovom d.d.f. ING Tatry - Sympatia, d.d.s., a.s. Bratislava, august 2007 VZOR Informácie o majetku v doplnkovom dôchodkovom fonde Dfo
Polroná správa k 30.6.2007 o hospodárení s majetkom v Rastovom príspevkovom d.d.f. ING Tatry - Sympatia, d.d.s., a.s. Bratislava, august 2007 VZOR Informácie o majetku v doplnkovom dôchodkovom fonde Dfo
Princípy tvorby softvéru Programovacie paradigmy
 Princípy tvorby softvéru lukotka@dcs.fmph.uniba.sk www.dcs.fmph.uniba.sk/~lukotka M-255 PTS - ƒo to je programovacia paradigma A programming paradigm is a style, or way, of programming. Paradigm can also
Princípy tvorby softvéru lukotka@dcs.fmph.uniba.sk www.dcs.fmph.uniba.sk/~lukotka M-255 PTS - ƒo to je programovacia paradigma A programming paradigm is a style, or way, of programming. Paradigm can also
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Optimálne navrhovanie experimentov DIPLOMOVÁ PRÁCA 2012 Bc. Samuel Zmeko
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Optimálne navrhovanie experimentov DIPLOMOVÁ PRÁCA 2012 Bc. Samuel Zmeko UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Optimálne navrhovanie experimentov DIPLOMOVÁ PRÁCA 2012 Bc. Samuel Zmeko UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
J&T BOND EUR o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s
 J&T BOND EUR o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.217 J&T BOND EUR
J&T BOND EUR o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.217 J&T BOND EUR
O možnosti riešenia deformácie zemského povrchu z pohladu metódy konecných prvkov konference pro studenty matematiky
 O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
1.pdf
 Ú FOND 1-02 31570020000000003475 Názov spravovaného fondu Globálny akciový dôchodkový fond AXA d.d.s., a.s., príspevkový d.d.f. SÚVAHA k 31.12.2015 v eurách Ozna enie POLOŽKA 31.12.2015 31.12.2014 a b
Ú FOND 1-02 31570020000000003475 Názov spravovaného fondu Globálny akciový dôchodkový fond AXA d.d.s., a.s., príspevkový d.d.f. SÚVAHA k 31.12.2015 v eurách Ozna enie POLOŽKA 31.12.2015 31.12.2014 a b
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UƒENIE INVARIANTNÝCH SENZO-MOTORICKÝCH REPREZENTÁCIÍ POHYBOV UCHOPOVANIA P
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UƒENIE INVARIANTNÝCH SENZO-MOTORICKÝCH REPREZENTÁCIÍ POHYBOV UCHOPOVANIA POMOCOU NEURÓNOVÝCH SIETÍ Diplomová práca 2018 Bc. Jakub
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UƒENIE INVARIANTNÝCH SENZO-MOTORICKÝCH REPREZENTÁCIÍ POHYBOV UCHOPOVANIA POMOCOU NEURÓNOVÝCH SIETÍ Diplomová práca 2018 Bc. Jakub
Priebeh funkcie
 Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
PS_J&T BOND EUR
 J&T BOND EUR o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.215 J&T BOND EUR
J&T BOND EUR o. p. f. PRVÁ PENZIJNÁ SPRÁVCOVSKÁ SPOLOČNOSŤ POŠTOVEJ BANKY, správ. spol., a.s. Polročná správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde k 3.6.215 J&T BOND EUR
Strana 5526 Zbierka zákonov č. 590/2003 Čiastka NARIADENIE VLÁDY Slovenskej republiky zo 17. decembra 2003 o skúškach odbornej spôsobilosti pr
 Strana 5526 Zbierka zákonov č. 590/2003 Čiastka 241 590 NARIADENIE VLÁDY Slovenskej republiky zo 17. decembra 2003 o skúškach odbornej spôsobilosti príslušníkov obecnej polície a o odbornej príprave príslušníkov
Strana 5526 Zbierka zákonov č. 590/2003 Čiastka 241 590 NARIADENIE VLÁDY Slovenskej republiky zo 17. decembra 2003 o skúškach odbornej spôsobilosti príslušníkov obecnej polície a o odbornej príprave príslušníkov
MergedFile
 BILANCIA AKTÍV A PASÍV Bil (NBS) 1-12 Názov banky/pobočky zahraničnej banky: Kód banky/pobočky zahraničnej banky: Hlásenie ku dňu: Druh hlásenia t1 Infinity Capital, o.c.p., a.s. S3103110028 30.06.2017
BILANCIA AKTÍV A PASÍV Bil (NBS) 1-12 Názov banky/pobočky zahraničnej banky: Kód banky/pobočky zahraničnej banky: Hlásenie ku dňu: Druh hlásenia t1 Infinity Capital, o.c.p., a.s. S3103110028 30.06.2017
Strana 5634 Zbierka zákonov č. 558/2002 Čiastka VYHLÁŠKA Ministerstva financií Slovenskej republiky zo 6. augusta 2002, ktorou sa ustanovuje r
 Strana 5634 Zbierka zákonov č. 558/2002 Čiastka 218 558 VYHLÁŠKA Ministerstva financií Slovenskej republiky zo 6. augusta 2002, ktorou sa ustanovuje rozsah, spôsob a termíny predkladania výkazov, hlásení
Strana 5634 Zbierka zákonov č. 558/2002 Čiastka 218 558 VYHLÁŠKA Ministerstva financií Slovenskej republiky zo 6. augusta 2002, ktorou sa ustanovuje rozsah, spôsob a termíny predkladania výkazov, hlásení
Ekon Supply of labour by John Pencavel
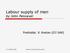 Labour supply of men by John Pencavel Prednáša: V. Kvetan (EÚ SAV) Obsah kapitoly Úvod Empirické regulácie Trendy v pracovnom správaní Cross sekčné odchýlky v pracovnom správaní Koncepčný rámec Kanonický
Labour supply of men by John Pencavel Prednáša: V. Kvetan (EÚ SAV) Obsah kapitoly Úvod Empirické regulácie Trendy v pracovnom správaní Cross sekčné odchýlky v pracovnom správaní Koncepčný rámec Kanonický
Meno: Škola: Ekonomická olympiáda 2017/2018 Test krajského kola SÚŤAŽ REALIZUJE PARTNERI PROJEKTU
 Meno: Škola: Ekonomická olympiáda 2017/2018 Test krajského kola SÚŤAŽ REALIZUJE PARTNERI PROJEKTU Ekonomická olympiáda Test krajského kola 2017/2018 Pokyny pre študentov: Test obsahuje štyri časti. Otázky
Meno: Škola: Ekonomická olympiáda 2017/2018 Test krajského kola SÚŤAŽ REALIZUJE PARTNERI PROJEKTU Ekonomická olympiáda Test krajského kola 2017/2018 Pokyny pre študentov: Test obsahuje štyri časti. Otázky
Študijný program (Študijný odbor) Školiteľ Forma štúdia Téma Elektronické zbraňové systémy (8.4.3 Výzbroj a technika ozbrojených síl) doc. Ing. Martin
 doc. Ing. Martin Marko, CSc. e-mail: martin.marko@aos.sk tel.: 0960 423878 Metódy kódovania a modulácie v konvergentných bojových rádiových sieťach Zameranie: Dizertačná práca sa bude zaoberať modernými
doc. Ing. Martin Marko, CSc. e-mail: martin.marko@aos.sk tel.: 0960 423878 Metódy kódovania a modulácie v konvergentných bojových rádiových sieťach Zameranie: Dizertačná práca sa bude zaoberať modernými
Operačná analýza 2
 Niektoré náhodné procesy majú v praxi veľký význam, pretože sa často vyskytujú, napr.: Poissonov proces proces vzniku a zániku Wienerov proces stacionárne procesy,... Poissonov proces je homogénny Markovov
Niektoré náhodné procesy majú v praxi veľký význam, pretože sa často vyskytujú, napr.: Poissonov proces proces vzniku a zániku Wienerov proces stacionárne procesy,... Poissonov proces je homogénny Markovov
ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30
 ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30 ARMA modely - motivácia I. Odhadneme ACF a PACF pre dáta a nepodobajú sa
ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30 ARMA modely - motivácia I. Odhadneme ACF a PACF pre dáta a nepodobajú sa
Preco kocka stací? - o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, ked sú velké
 o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
Žiadosť o prídavok na dieťa
 A Údaje o žiadate ovi Žiados o prídavok na die a Údaje v žiadosti vyp ajte pali kovým písmom a zodpovedajúci údaj ozna te pod a tohto vzoru Priezvisko Meno Rodinný stav 1) Dátum narodenia Rodné íslo (Identifika
A Údaje o žiadate ovi Žiados o prídavok na die a Údaje v žiadosti vyp ajte pali kovým písmom a zodpovedajúci údaj ozna te pod a tohto vzoru Priezvisko Meno Rodinný stav 1) Dátum narodenia Rodné íslo (Identifika
Matematicko-fyzikálna fakulta Univerzity Karlovej v Prahe SPRÁVA O TUDENTSKOM FAKULTNOM GRANTE Marek Martaus Testování prototyp modul vnit ního detekt
 Matematicko-fyzikálna fakulta Univerzity Karlovej v Prahe SPRÁVA O TUDENTSKOM FAKULTNOM GRANTE Marek Martaus Testování prototyp modul vnit ního detektoru ATLAS v CERN Ústav jadrovej a asticovej fyziky
Matematicko-fyzikálna fakulta Univerzity Karlovej v Prahe SPRÁVA O TUDENTSKOM FAKULTNOM GRANTE Marek Martaus Testování prototyp modul vnit ního detektoru ATLAS v CERN Ústav jadrovej a asticovej fyziky
Snímka 1
 Fyzika - prednáška 8 Ciele 3. Kmity 3.1 Netlmený harmonický kmitavý pohyb 3. Tlmený harmonický kmitavý pohyb Zopakujte si Výchylka netlmeného harmonického kmitavého pohybu je x = Asin (ω 0 t + φ 0 ) Mechanická
Fyzika - prednáška 8 Ciele 3. Kmity 3.1 Netlmený harmonický kmitavý pohyb 3. Tlmený harmonický kmitavý pohyb Zopakujte si Výchylka netlmeného harmonického kmitavého pohybu je x = Asin (ω 0 t + φ 0 ) Mechanická
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 Jednotkový koreň(unit roo
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Microsoft Word - BE_RTS_28_2018_SK_PROF.docx
 Úvod UniCredit Bank Czech Republic and Slovakia, a.s., pobočka zahraničnej banky, so sídlom Šancová 1/A, 813 33 Bratislava, IČO: 47 251 336, zapísaná v obchodnom registri Okresného súdu Bratislava I, oddiel:
Úvod UniCredit Bank Czech Republic and Slovakia, a.s., pobočka zahraničnej banky, so sídlom Šancová 1/A, 813 33 Bratislava, IČO: 47 251 336, zapísaná v obchodnom registri Okresného súdu Bratislava I, oddiel:
OTP Banka Slovensko, a.s., Štúrova 5, Bratislava IČO: V ÝR O Č N Á S P R Á V A za rok 2018 (v zmysle 77 zákona o cenných papieroch) Br
 OTP Banka Slovensko, a.s., Štúrova 5, 813 54 Bratislava IČO: 31318916 V ÝR O Č N Á S P R Á V A za rok 2018 (v zmysle 77 zákona o cenných papieroch) Bratislava, 26. apríla 2019 a) INDIVIDUÁLNA ÚČTOVNÁ ZÁVIERKA
OTP Banka Slovensko, a.s., Štúrova 5, 813 54 Bratislava IČO: 31318916 V ÝR O Č N Á S P R Á V A za rok 2018 (v zmysle 77 zákona o cenných papieroch) Bratislava, 26. apríla 2019 a) INDIVIDUÁLNA ÚČTOVNÁ ZÁVIERKA
Microsoft PowerPoint - Horniaček_Prezentácia_Transferové oceňovanie
 Rozšírenie pravidiel transferového oceňovania na vzťahy medzi tuzemskými závislými osobami od 1.1.2015 - základný právny rámec po novele ZDP č. 333/2014 Z. z., príp. 253/2015 Z. z. 1 Transferové oceňovanie
Rozšírenie pravidiel transferového oceňovania na vzťahy medzi tuzemskými závislými osobami od 1.1.2015 - základný právny rámec po novele ZDP č. 333/2014 Z. z., príp. 253/2015 Z. z. 1 Transferové oceňovanie
Štatúty NOVIS Poistných Fondov ŠTATÚT NOVIS GARANTOVANE RASTÚCI POISTNÝ FOND 1. Základné ustanovenia NOVIS Garantovane Rastúci Poistný Fond vytvára a
 ŠTATÚT NOVIS GARANTOVANE RASTÚCI POISTNÝ FOND NOVIS Garantovane Rastúci Poistný Fond vytvára a spravuje NOVIS Poisťovňa a.s., so sídlom Námestie Ľudovíta Štúra 2, 811 02 Bratislava, Úplné označenie fondu
ŠTATÚT NOVIS GARANTOVANE RASTÚCI POISTNÝ FOND NOVIS Garantovane Rastúci Poistný Fond vytvára a spravuje NOVIS Poisťovňa a.s., so sídlom Námestie Ľudovíta Štúra 2, 811 02 Bratislava, Úplné označenie fondu
Vzhľadom k tomu, že Žiadosť o platbu č
 Postup na identifikáciu žiadateľa ako podniku v ťažkostiach podľa Usmernenia Spoločenstva o štátnej pomoci na záchranu a reštrukturalizáciu firiem v ťažkostiach (2004/C244/02) Pred tým, ako bude uvedený
Postup na identifikáciu žiadateľa ako podniku v ťažkostiach podľa Usmernenia Spoločenstva o štátnej pomoci na záchranu a reštrukturalizáciu firiem v ťažkostiach (2004/C244/02) Pred tým, ako bude uvedený
Operačná analýza 2
 Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Modelovanie nového produktu na trhu: Bassov model Beáta Stehlíková Cvičenia z časových radov, FMFI UK Modelovanie nového produktu na trhu: Bassov mode
 Modelovanie nového produktu na trhu: Bassov model Beáta Stehlíková Cvičenia z časových radov, FMFI UK Modelovanie nového produktu na trhu: Bassov model p.1/19 Úvod Frank Bass (1926-2006) - priekopník matematických
Modelovanie nového produktu na trhu: Bassov model Beáta Stehlíková Cvičenia z časových radov, FMFI UK Modelovanie nového produktu na trhu: Bassov model p.1/19 Úvod Frank Bass (1926-2006) - priekopník matematických
