Zbierka úloh z Matematiky 2
|
|
|
- Júlia Stárková
- pred 1 rokmi
- Prehliadani:
Prepis
1 Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Zbierka úloh z Matematiky Anna Grinčová Jana Petrillová Košice 09
2
3 Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Zbierka úloh z Matematiky Anna Grinčová Jana Petrillová Košice 09
4 Recenzovali: RNDr. Miriam Andrejiová, PhD. doc. RNDr. Viktor Pirč, CSc.. vydanie Za odbornú stránku učebného textu zodpovedajú autori. Rukopis neprešiel redakčnou ani jazykovou úpravou. c Anna Grinčová, Jana Petrillová ISBN
5 Obsah Úvod 6 Nekonečné rady 7. Pojem nekonečného číselného radu a jeho súčet Harmonický a geometrický rad Kritériá konvergencie číselných radov Funkcionálne a mocninové rady Diferenciálny počet funkcie viacerých premenných 6. Funkcia n premenných Parciálne derivácie funkcie n premenných Parciálne derivácie zloženej funkcie Dotyková rovina Lokálne extrémy funkcie n premenných Viazané extrémy funkcie dvoch premenných Diferenciálne rovnice 57. Diferenciálne rovnice prvého rádu so separovateľnými premennými Lineárne diferenciálne rovnice prvého rádu Lineárne diferenciálne rovnice druhého rádu s konštantnými koeficientmi Funkcia komplexnej premennej Analytická funkcie a derivácia funkcie komplexnej premennej Rezíduum funkcie Integrál funkcie komplexnej premennej Laplaceova transformácia Laplaceova transformácia Spätná Laplaceova transformácia Riešenie diferenciálnych rovníc pomocou spätnej Laplaceovej transformácie.. 9 Použitá literatúra 99
6 6 Úvod Táto učebná pomôcka je určená pre študentov prvého ročníka bakalárskej formy štúdia Fakulty elektrotechniky a informatiky Technickej univerzity v Košiciach (FEI TU), ale môže poslúžiť aj študentom iných fakúlt. Učebnica je rozdelená do piatich kapitol, ktoré obsahujú základné teoretické poznatky potrebné k riešeniu príkladov, vzorové riešené aj neriešené úlohy k učivu, ktoré je preberané v predmete Matematika II. Cieľom tejto učebnej pomôcky nebolo podať ucelený teoretický prehľad riešenej problematiky, preto je vhodné kombinovať používanie tejto učebnice s vysokoškolskou učebnicou Matematická analýza II autorov Jozef Džurina, Anna Grinčová a Viktor Pirč aj s voľne dostupnými e-learningovými materiálmi Katedry matematiky a teoretickej informatiky FEI TU v Košiciach. Na záver ďakujeme RNDr. Miriam Andrejiovej, PhD. a doc. RNDr. Viktorovi Pirčovi CSc. za starostlivé prečítanie rukopisu a za cenné pripomienky, ktorými prispeli k zlepšeniu textu tejto učebnice. Zároveň sa chceme vopred ospravedlniť za možné jazykovo-štylistické chyby, pretože daný text neprešiel redakčnou ani jazykovou úpravou.
7 7 Nekonečné rady. Pojem nekonečného číselného radu a jeho súčet Definícia. Nech {a n } je postupnosť reálnych čísel. Potom výraz a n = a + a + + a n + nazývame nekonečný číselný rad, kde číslo a n nazývame n tým členom nekonečného číselného radu. Definícia. Postupnosť {s n } definovanú s = a, s = a + a, s = a + a + a,..., s n = a + a + + a n nazývame postupnosť čiastočných súčtov. Definícia. Ak existuje konečná ita s = s n, tak číslo s nazývame súčtom radu a n a hovoríme, že rad a n je konvergentný. Označujeme s = a n. Definícia.4 Ak neexistuje konečná ita s n, tak je rad a n divergentný. Definícia.5 Ak je nekonečný číselný rad a n = a + a + + a n + konvergentný, tak hovoríme, že nekonečný číselný rad a n je absolútne konvergentný. Definícia.6 Ak je nekonečný číselný rad a n konvergentný a rad a n je divergentný, tak hovoríme, že nekonečný číselný rad a n je relatívne konvergentný. Veta. Ak je rad a n absolútne konvergentný, tak je rad a n konvergentný. Veta. (Nutná podmienka konvergencie nekonečného číselného radu) Ak je rad a n konvergentný, tak a n = 0. Príklad. Nájdime súčet radu n + n +. Riešenie: Najprv urobíme rozklad n tého člena radu na súčet elementárnych zlomkov. Z toho vyplýva n + n + = (n + )(n + ) = ( n + ). n +
8 8 NEKONEČNÉ RADY Teda n tý čiastočný súčet je ( s n = ) ( + ) ( ) ( n ) ( + n n ) ( + n + n + ). n + Vidíme, že niektoré členy sa odčítajú, preto po úprave dostaneme s n = n +. Súčet radu je ( s = s n = ) = n +.. Harmonický a geometrický rad Zovšeobecnený harmonický rad má tvar n α pre α > 0. Tento rad je divergentný pre α a konvergentný pre α >. Špeciálnym prípadom zovšeobecneného harmonického radu pre α = je harmonický rad a má tvar. Tento rad je divergentný. n Geometrický rad má tvar a q n = a +a q +a q + +a q n +, kde a 0. Tento rad n=0 je konvergentný pre q < a divergentný pre q. Súčet nekonečného geometrického radu je s = a, kde q <. q Príklad. Nájdime súčet radu ( n ( ) ) n+. n= Riešenie: Pre daný rad určíme prvý člen a a kvocient q. Prvý člen a získame dosadením n = do n-tého člena radu Kvocient q určíme takto a = ( ) + ( q = a n+ a n ) = 4 9. ( n+ = ) ( )n+ ( ) ( ) n+ n =. Pretože platí q = <, súčet tohto geometrického radu je s = a q = 4 9 ( ) = 4 5.
9 . Kritériá konvergencie číselných radov 9. Kritériá konvergencie číselných radov Veta. (D Alembertovo podielové kritérium) Nech a n je nekonečný číselný rad a nech n N platí, že a n 0. (a) Ak (b) Ak a n+ a n a n+ a n <, tak je rad a n absolútne konvergentný. >, tak je rad a n divergentný. Príklad. Vyšetrime konvergenciu radu ( Riešenie: n tý člen radu je rovný a n = n Na základe D Alembertovho kritéria dostávame ( a n+ n+ a n = n+ ( ) n = ) n n ( ) n. ) n a (n+) člen radu je rovný an+ = n+ Z toho vyplýva, že daný číselný rad konverguje. Veta.4 (Cauchyho odmocninové kritérium) Nech a n je nekonečný číselný rad. n n + = n n + = <. (a) Ak n a n <, tak je rad a n absolútne konvergentný. (b) Ak n a n >, tak je rad a n divergentný. ( ) n+ n Príklad.4 Vyšetrime konvergenciu radu. 5n + ( ) n+. Riešenie: n tý člen radu je rovný a n = ( n n+. 5n+) Na základe Cauchyho odmocninového kritéria dostávame n n an = = = ( 5 ( n 5n + ( ) ( n n. 5n + 5n + ) ( ) 0 = <. ) n+ ( n = ) n Z toho vyplýva, že daný číselný rad konverguje. 5n + = ) n+ n ( n 5n + ( n = ). 5n + ( n 5n + ) + n = ) n =
10 0 NEKONEČNÉ RADY Poznámka: Ak jednotlivé ity pri D Alembertovom podielovom kritériu a Cauchyho odmocninovom kritériu sú rovné, potom pomocou týchto kritérií nevieme rozhodnúť, či daný rad je konvergentný alebo divergentný. Musíme teda použiť iné kritérium. Veta.5 (Cauchyho integrálne kritérium) Nech pre rad f(n) = a n. a n existuje spojitá funkcia f(x) nerastúca na K, ) a nech n > K: (a) Ak K (b) Ak K f(x)dx <, tak je rad a n absolútne konvergentný. f(x)dx =, tak rad je a n divergentný. Príklad.5 Vyšetrime konvergenciu radu n= n ln n. Riešenie: Položme f(x) =. Definičný obor tejto funkcie je D(f) = (0, ) {}. Funkcia x ln x je teda spojitá na intervale, ). Je zrejmé, že pre každé n je f(n) = = a n. Pretože f (+ln x) (x) = < 0, je funkcia f(x) klesajúca na intervale, ) a možno teda (x ln x) použiť Cauchyho integrálne kritérium. Platí x ln x a dx = a = a (ln ln a ln ln ) = Z toho vyplýva, že daný číselný rad diverguje. dx = x ln x [ln ln a x ]a = a ln ln a ln =. =. n ln n Veta.6 (Leibnizovo kritérium) Nech ( ) n+ a n je rad so striedavými znamienkami. Nech postupnosť {a n } je nerastúca. Potom rad ( ) n+ a n je konvergentný práve vtedy, ak a n = 0. Príklad.6 Vyšetrime konvergenciu radu Riešenie: ( ) n+. n ( ) n+ n je rad so striedavými znamienkami, kde a n = n. Naviac platí n N : n < n + n < (n + ) n < (n + ) n > (n + ).
11 . Kritériá konvergencie číselných radov Postupnosť {a n } pre a n = n n = 0, podľa Leibnizovho kritéria je rad Definícia.7 Majme rady a n, je klesajúca, z čoho vyplýva, že je aj nerastúca. Keďže ( ) n+ n konvergentný. b n, pričom b n 0 pre všetky n N. Rad b n na- zývame majorantný rad k radu a n a rad a n nazývame minorantný rad k radu b n, ak pre každé n N a n b n. Veta.7 (Majorantné porovnávacie kritérium) Majme rady a n a b n, kde 0 a n b n pre n =,,.... Ak majorantný rad b n konverguje, tak konverguje aj rad a n. Ak minorantný rad a n diverguje, tak diverguje aj rad b n. Veta.8 (Limitné porovnávacie kritérium) Nech pre každé n N je a n 0 a b n > 0. a (a) Ak existuje vlastná ita n bn a rad b n konverguje, tak konverguje aj rad a n. a (b) Ak existuje vlastná ita n bn rôzna od nuly alebo je táto ita nevlastná a rad b n diverguje, tak diverguje aj rad a n. Poznámka: Použitie porovnávacieho kritéria vyžaduje skúsenosti na skonštruovanie majorantného resp. minorantného radu na základe hypotézy o konvergencii, resp. divergencii vyšetrovaného radu. Často sa používa na toto porovnávanie zovšeobecnený harmonický rad. Príklad.7 Vyšetrime konvergenciu radu n + n + 4n. Riešenie: n tý člen radu je rovný a n = n+. Skúsime porovnať daný rad s harmonickým n +4n radom, o ktorom vieme, že je divergentný. Teda položíme b n n =. Keďže platí n a n = b n n+ n +4n n Podľa itného porovnávacieho kritéria je aj rad Príklad.8 Vyšetrime konvergenciu radu = n(n + ) n + 4n = 0. n+ divergentný. n +4n n + 4n n 5 n +.
12 NEKONEČNÉ RADY Riešenie: n tý člen radu je rovný a n = n +4n n 5 n+. Skúsime porovnať daný rad s radom o ktorom vieme, že je konvergentný. Teda položíme b n = n. Keďže platí a n = b n n +4n n 5 n+ n n (n + 4n) = n 5 n + = n 5 + 4n 4 n 5 n + =. Táto ita je vlastná a podľa itného porovnávacieho kritéria je rad n +4n konver- n 5 n+ gentný., n.4 Funkcionálne a mocninové rady Definícia.8 Nech {f n (x)} je postupnosť funkcií definovaných na intervale a, b, potom výraz f n (x) nazývame nekonečný funkcionálny rad. Pre konvergenciu funkcionálnych radov môžeme použiť upravené D Alembertovo podielové a Cauchyho odmocninové kritérium. Teda ak f n+(x) n f n(x) < resp. fn (x) <, tak funkcionálny rad konverguje v x. Definícia.9 Ak f n (x) = a n (x a) n, rad stredom v bode a. n=0 a n (x a) n Pre každý mocninový rad a n (x a) n nastáva jeden z prípadov: n=0 rad konverguje len v bode x = a ρ = 0, rad konverguje pre x R ρ =, nazývame mocninový rad so ρ > 0, že na intervale (a ρ, a + ρ) daný rad konverguje a na množine R/ a ρ, a + ρ daný rad diverguje. Číslo ρ sa nazýva polomer konvergencie a interval (a ρ, a + ρ) označuje interval konvergencie. Ak existuje a n+ a n = λ resp. n a n = λ, tak pre polomer konvergencie mocninového radu a n (x a) n platí n=0 ρ = λ pre 0 < λ <, ρ = pre λ = 0, ρ = 0 pre λ =.
13 .4 Funkcionálne a mocninové rady Príklad.9 Nájdime interval, na ktorom mocninový rad Riešenie: Riešenie tejto úlohy urobíme dvoma spôsobmi. (x + ) n n (n + )(n + ) konverguje. Riešenie spôsobom A: Použijeme D Alembertovo kritérium pre konvergenciu funkcionálnych radov. f n (x) = f n+ (x) f n (x) (x+)n a f n (n+)(n+) n+(x) = (x+)n+. Potom n+ (n+)(n+) = (x+) n+ n+ (n+)(n+) (x+) n n (n+)(n+) = (n + ) (x + ) (n + ) = x +. f Podľa D Alembertovho kritéria je rad konvergentný vtedy, ak platí n+ (x) f n(x) <. Pre daný rad teda musí platiť podmienka x + <, z čoho dostávame x + < < (x + ) < < x + < 5 < x <. Pre všetky x ( 5, ) rad (x+) n n (n+)(n+) konverguje. Ešte musíme vyšetriť konvergenciu radu v krajných hodnotách a k tomu použijeme kritériá konvergencie číselných radov.. Pre x = 5 dostaneme číselný rad ( ) n n (n + )(n + ) = ( ) n (n + )(n + ). Dostávame rad so striedavými znamienkami, kde a n = { kritéria zistíme, či daný rad konverguje. O postupnosti nerastúca a keďže = 0, rad ( ) n (n+)(n+) (n+)(n+). Pre x = dostaneme číselný rad (n+)(n+) (n+)(n+) a podľa Leibnizovho } je konvergentný. n n (n + )(n + ) = (n + )(n + ). vieme, že je Daný číselný rad má súčet s = (pozri Príklad.) a teda je konvergentný. Obor konvergencie radu (x + ) n n (n + )(n + ) je interval 5,. Riešenie spôsobom B: D Alembertovo kritérium použijeme na určenie polomeru konvergencie mocninového radu. a n = n (n+)(n+) a a n+ = n+ (n+)(n+). Potom λ = a n+ a n = n+ (n+)(n+) n (n+)(n+) = (n + ) (n + ) =.
14 4 NEKONEČNÉ RADY Polomer konvergencie ρ = =. Stred radu je a =. Interval konvergencie je (a ρ, a+ρ) = λ (, + ) = ( 5, ). Konvergenciu radu v krajných hodnotách určíme rovnako ako v (x + ) n Riešení A. Obor konvergencie radu je interval 5,. n (n + )(n + ) Príklad.0 Nájdime interval, na ktorom mocninový rad x n 4 n konverguje. n Riešenie: Daný mocninový rad má stred v bode a = 0 a a n = 4n. Cauchyho odmocninové n kritérium použijeme na určenie polomeru konvergencie mocninového radu a využijeme vzťah n n =. Platí λ = n n a n = 4 n n = 4 n = 4 n n = 4. n Polomer konvergencie ρ = =. Stred radu je a = 0. Interval konvergencie je (a ρ, a + λ 4 ρ) = (0 4, ) = ( 4, 4 ). Ešte musíme vyšetriť konvergenciu radu v krajných hodnotách a k tomu použijeme kritériá konvergencie číselných radov.. Pre x = 4 dostaneme číselný rad ( ) n n. Dostávame rad so striedavými znamienkami, kde a n = a podľa Leibnizovho kritéria n zistíme, či daný rad konverguje. O postupnosti { n} vieme, že je nerastúca a keďže = 0, rad ( ) n je konvergentný. n n. Pre x = 4 dostaneme číselný rad n. Tento rad je harmonický rad, preto je divergentný. x n 4 n Obor konvergencie radu je interval n 4, ). 4 Veta.9 (Veta o derivovaní a integrovaní mocninového radu) Nech ρ > 0 je polomer konvergencie mocninového radu a n (x a) n a nech funkcia s(x) = x (a ρ, a + ρ). Potom pre každé x (a ρ, a + ρ) platí n=0 a n (x a) n,
15 .4 Funkcionálne a mocninové rady 5 s (x) = n a n (x a) n, x s(t) dt = a n=0 a n (x n+ a)n+. Príklad. Derivovaním alebo integrovaním vhodného radu nájdime súčet radu na vhodnom intervale. n x n Riešenie: Keďže platí (x n ) = nx n, môžeme napísať ( ) n x n = x n. Rad x n je geometrický rad, kde a = x, q = x, a teda tento rad je konvergentný pre x <. Potom súčet tohto geometrického radu je s = a q = je rovný s = ( ) x = x ( x) pre x (, ). x. Teda súčet radu x n x n Definícia.0 Nech funkcia f(x) má v bode a derivácie všetkých rádov. Mocninový rad f (n) (a) (x a) n = f(a) + f (a) (x a) + f (a) (x a) + + f (n) (a) (x a) n + n!!! n! n=0 nazývame Taylorov rad funkcie so stredom v bode a. Uvedieme rozvoj niektorých funkcií do Taylorovho radu so stredom v bode a = 0: ln( + x) = sin x = cos x = e x = n=0 x n n! ( ) n=0 n+ xn pre x R, n ( ) n x n+ (n + )! ( ) n xn (n)! n=0 pre x (,, pre x R, pre x R.
16 6 NEKONEČNÉ RADY Príklad. Rozviňme funkciu f(x) = x ln( + x ) do Taylorovho radu. Riešenie: Ak namiesto x dosadíme x do vzťahu ln( + x) = ( ) n+ xn, dostaneme n ln( + x ) = ( ) Potom vynásobíme obe strany x a úpravou dostaneme n+ xn n. x ln( + x ) = x ( ) n+ xn n = ( ) n+ xn+ n pre x (,. Príklad. Nájdime prvé tri členy rozvoja funkcie f(x) = x e x do Taylorovho radu v bode a = 0. Riešenie: Z definície Taylorovho radu vyplýva f(x) f(0) + f (0)! (x 0) + f (0)! (x 0) + f (0)! (x 0) x e x. Keďže platí f (x) = e x + x e x f (0) =, f (x) = e x + e x + x e x = e x + x e x f (0) =, f (x) = e x + e x + x e x = e x + x e x f (0) =, rozvoj funkcie f(x) = x e x do Taylorovho radu v bode a = 0 je x e x 0 +! x +! x +! x. Definícia. Nech f(x), x l, l je po častiach spojitá, periodická funkcia s periódou T = l. Trigonometrický rad a 0 + a n cos πnx l + b n sin πnx, l kde a 0 = l l l f(x) dx,
17 .4 Funkcionálne a mocninové rady 7 a n = l l l f(x) cos πnx l dx, b n = l l l f(x) sin πnx l n =,,..., nazývame Fourierov rad funkcie f(x) a píšeme f(x) a 0 + ( a n cos πnx l dx, Koeficienty a 0, a n a b n nazývame Fourierove koeficienty. + b n sin πnx ). l Definícia. Nech f(x), x l, l je po častiach spojitá, párna, periodická funkcia s periódou T = l. Trigonometrický rad kde a 0 a n = l + l 0 a n cos πnx, l f(x) cos πnx dx, l n = 0,,..., nazývame kosínusový Fourierov rad funkcie f(x). Definícia. Nech f(x), x l, l je po častiach spojitá, nepárna, periodická funkcia s periódou T = l. Trigonometrický rad kde b n = l l 0 b n sin πnx, l f(x) sin πnx dx, l n =,,..., nazývame sínusový Fourierov rad funkcie f(x). V praxi sa stretávame s dejmi, ktoré sa pravidelne opakujú. Sú to tzv. periodické deje, ktoré možno popísať periodickými funkciami. Ak f(x) je periodická funkcia s periódou T, tak a D(f) platí a+t f(x) dx = T f(x) dx. a 0
18 8 NEKONEČNÉ RADY Fourierove rady sú funkcionálne rady, ktorými popisujeme periodicky sa opakujúce deje. Ak chceme pomocou kosínusového resp. sínusového Fourierovho radu vyjadriť po častiach spojitú funkciu f(x), ktorá nie je ani párna ani nepárna, musíme ju najprv párne resp. nepárne predĺžiť: Párne predĺženie funkcie f(x) z intervalu 0, l na interval l, l sa nazýva funkcia { f(x) pre x 0, l, f p (x) = f( x) pre x l, 0. Nepárne predĺženie funkcie f(x) z intervalu 0, l na interval l, l sa nazýva funkcia f(x) pre x (0, l, f n (x) = 0 pre x = 0, f( x) pre x l, 0). Príklad.4 Nájdime Fourierov rad funkcie f(x) = x + na intervale x,. Riešenie: Zo zadania vyplýva, že perióda je T = l =. Funkcia f(x) = x + nie je na intervale x, ani párna ani nepárna a pre n =,,... platí a 0 = l a n = l = l l l l f(x) dx = f(x) cos πnx l [ (x + ) sin(πnx) πn b n = l = l l [ x (x + ) dx = + x dx = ] f(x) sin πnx l [ (x + ) cos(πnx) πn dx = ] ] = + + = u = x + u = (x + ) cos(πnx) dx = v = cos(πnx) + sin(πnx) πn v = sin(πnx) πn = [ dx = cos(πnx) ] = cos(πn) cos( πn) = 0 π n π n π n u = x + u = (x + ) sin(πnx) dx = v = sin(πnx) cos(πnx) πn dx = ( )n πn = ( )n = ( )n+ πn πn Dosadením do predpisu Fourierovho radu dostávame f(x) a 0 + ( a n cos πnx + b n sin πnx ) = + l l [ sin(πnx) + π n [ ( ) n+ πn v = cos(πnx) πn ] ] sin(πnx). =
19 .4 Funkcionálne a mocninové rady 9 Príklad.5 Rozviňme funkciu f(x) = 4 x, x 0, π do kosínusového Fourierovho radu. Riešenie: Pretože hľadáme kosínusový Fourierov rad, musíme funkciu f(x) najprv dodefinovať tak, aby bola na rozšírenom intervale párna. Dostávame párnu funkciu { 4 x pre x 0, π, f p (x) = 4 + x pre x π, 0. y 4 π π x Obr. : Graf funkcie f p (x) Takto dodefinovaná funkcia má periódu T = π l = π a pre n =,,... platí a 0 = l l 0 l f(x) dx = π a n = l 0 u = 4 x = v = cos(nx) = [ cos(nx) π n b n = 0. π f(x) cos πnx dx = l π ] π 0 0 (4 x) dx = π u = v = sin(nx) = π π 0 ] π [4x x = 0 π (4 x) cos πnx π = π n ( cos(πn) + cos 0 n n dx = π [ (4 x) sin(nx) n ) ] π ) (4π π = 8 π, π π (4 x) cos(nx) dx = π = πn [ ( )n ], Dosadením do predpisu kosínusového Fourierovho radu dostávame 0 sin(nx) n dx = f(x) a 0 + a n cos πnx l = 8 π + πn [ ( )n ] cos(nx).
20 0 NEKONEČNÉ RADY Príklad.6 Rozviňme funkciu f(x) = 4 x, x 0, π do sínusového Fourierovho radu. Riešenie: Pretože hľadáme sínusový Fourierov rad, musíme funkciu f(x) najprv dodefinovať tak, aby bola na rozšírenom intervale nepárna. Dostávame nepárnu funkciu 4 x pre x (0, π, f n (x) = 0 pre x = 0, 4 x pre x π, 0). y 4 π 4 π x Obr. : Graf funkcie f n (x) Takto dodefinovaná funkcia má periódu T = π l = π a pre n =,,... platí a n = 0, l π b n = f(x) sin πnx dx = (4 x) sin πnx l l π π dx = (4 x) sin(nx) dx = π u = 4 x u = = v = sin(nx) v = cos(nx) = [ (4 x) cos(nx) ] π π cos(nx) dx = π n n 0 π n 0 = [ (π 4) cos(nπ) + 4 ] [ ] π sin(nx) = π n n π n πn [(π 4) ( )n + 4]. Dosadením do predpisu sínusového Fourierovho radu dostávame 0 π f(x) b n sin πnx l = πn [(π 4) ( )n + 4] sin(nx).
21 .4 Funkcionálne a mocninové rady Neriešené úlohy: V nasledujúcich úlohách nájdite súčet radu: n=0 (n + )(n + ) (5n 4)(5n + ) (n )(n + ) n + 5n + 6 n + 7n + n + 9n + 0 n + 4n + n + 6n + 8 n + 8n + 5 n + 0n + 4 n + n n + 5n + 4 4n + 8n + 9n + n 9n n 7 49n 7n 7 49n n n + n
22 NEKONEČNÉ RADY n= n= n=5 n= n= 9n + n 5 4 9n n 5 6 9n + 6n 8 6n n 5 n 6 4n 9 (n )(n 4) n n(n + )(n + ) n + n(n )(n ) (n + n + )(n + ) n + n + n n + n + n n n + n + n n + n n + n 5 n n 5 n ( ) n n 4 ( ) n n
23 .4 Funkcionálne a mocninové rady n=0 0 4 n+ 5 6 n n+ n=0 n+ 7 4 n n= ( ) n 5 ( ) n 5 7 ( ) n n+ 8 n 5 n= ( ) n+ ( ) n 45 n= ( ) n n+ ( ) n n+ ( ) 5 n n+ 6 4 n n n 6 n n 5 n + n 6 n 5 n 4 V nasledujúcich úlohách vyšetrite pomocou D Alembertovho kritéria konvergenciu radu: ( ) n n 8 ( ) n n + ( ) n 5 n 7 ( ) n 6 n + 5 ( ) n (n + )! 4 ( ) n 7 n 5 a n+ a n =, konverguje 8 a n+ a n =, konverguje a n+ a n = 5, konverguje 7 a n+ a n = 6, diverguje 5 a n+ a n = 0, konverguje a n+ a n = 7, diverguje 5
24 4 NEKONEČNÉ RADY n= n= 4n + n. n ( ) n 5 a n+ a n =, konverguje 5 n n n + n. n. n n + 4 a n+ a n a n+ a n a n+ a n (n ) n n (n + ) n (n + 4) n n n! n + n (n )!. 0 n. n! (n + )! n (n )! 5 n n! n! n (n + ) 6 n (n ) n! n (n + )! n n (n + )! ( ) n (n )! 7 n! ( ) n n 7 (n + )! (n!) (n)! a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n =, konverguje =, konverguje =, konverguje =, diverguje =, konverguje =, konverguje =, diverguje = 0, konverguje = 0, konverguje = 0, diverguje = 5, konverguje =, diverguje = 0, konverguje =, diverguje = 0, konverguje = 7, konverguje = 0, konverguje = 4, konverguje
25 .4 Funkcionálne a mocninové rady n! (n)! n (n)! (n + )! n (n + 5) n! n n n n (n!) n (n + )! n n! n n n n! n n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n a n+ a n (n + )! 0 n n. 0 n. n! (n)! a n+ a n a n+ a n n e n n n n! n n (n + )! ( ) n (n + )! ( ) n n (n + )! ( ) n n a n+ a n a n+ a n a n+ a n a n+ a n e n n + n (n )! a n+ a n a n+ a n (n )! 0 n+ (n )!. 0 n+ a n+ a n a n+ a n a n+ a n = 0, konverguje = 0, konverguje =, diverguje = e, konverguje = 0, konverguje = 0, konverguje = e, konverguje = e, diverguje =, diverguje = 0, konverguje = e, konverguje = e, konverguje = 6, diverguje = 0, konverguje = e, konverguje = 0, konverguje =, diverguje =, diverguje V nasledujúcich úlohách vyšetrite pomocou Cauchyho odmocninového kritéria konvergenciu radu:
26 6 NEKONEČNÉ RADY n a n n =, konverguje 4 ( + ) n an = n, konverguje n 6 ( ) n n + n an =, konverguje n ( 4n + n 5 n= ( n 4n ( 5n n + arctg n n ( n n + ( 8n + n ( n + 5 n ( n + n + ( 4n + n ( 0n + n ( n n + ( n + n ( 5n + n n ( n ( n + 5 n ( n n + n= ) n ) n ) n ) n ) n + ) n+ ) n ) n+ ) n+ ) n+ ) n ) n ) n ) n+ ) n n an =, diverguje n an =, konverguje 4 n an = 5, diverguje n an = 0, konverguje n an = 4, konverguje 9 n a n =, diverguje n an =, konverguje 9 n an = 4, konverguje 9 n an = 4, diverguje n an = 0, diverguje n an =, konverguje 9 n an =, konverguje n 5 an =, diverguje n an =, konverguje e n an = e 7, diverguje n an =, konverguje e 4
27 .4 Funkcionálne a mocninové rady n ) n ( n + n ( n + n + ( + n ) n ) n ( ) n ( 6 + ) n 5 n ( ) n ( ) n n + 7 n n an = e 0, diverguje n an =, diverguje n an = e, konverguje n an = 6e, diverguje 5 n an = e, konverguje 7 (n ) n n n n n a n = e, konverguje (n + ) n n n n n a n = e, konverguje n (n + ) n n a n n = e, diverguje (n + ) n V nasledujúcich úlohách vyšetrite pomocou Cauchyho integrálneho kritéria konvergenciu radu: n= n= n= 4n + n 5 n + 4n + 7 diverguje diverguje diverguje diverguje n + n diverguje n n + n n n + n n + diverguje diverguje konverguje konverguje
28 8 NEKONEČNÉ RADY n + n n n + n= n= n= n + 9 n 4 n 4 7n + n 6 n ln n n ln n ln n n ln n n ln n n e n n diverguje diverguje diverguje konverguje konverguje diverguje konverguje diverguje konverguje diverguje konverguje V nasledujúcich úlohách vyšetrite pomocou Leibnizovho kritéria konvergenciu radu: ( ) n+ n ( ) n+ ln(n + ) ( ) n+ (n + ) n + ( ) n+ n ( ) n+ n ( ) n+ (n + ) n ( ) n+ (n) n a n = 0, konverguje a n = 0, konverguje a n =, diverguje a n = 0, konverguje a n = 0, konverguje a n =, diverguje a n =, diverguje
29 .4 Funkcionálne a mocninové rady ( ) n+ n ln n ( ) n+ n n= a n = 0, konverguje n a n = 0, konverguje ( ) n+ sin π n a n = 0, konverguje V nasledujúcich úlohách vyšetrite pomocou porovnávacieho kritéria konvergenciu radu: n= n= n= 4n + n 5 n + 4n + 7 diverguje diverguje diverguje diverguje n + n diverguje n n + n n n + n 4 n + 9 n 4 n 4 7n + n 6 n,6 5 n n 7 n diverguje diverguje konverguje konverguje konverguje konverguje konverguje konverguje diverguje diverguje
30 0 NEKONEČNÉ RADY ( ) n 5 konverguje 7 ( ) n 7 diverguje 5 ( ) n konverguje n+ konverguje 6 4 n 5 n n diverguje V nasledujúcich úlohách nájdite interval, na ktorom daný funkcionálny rad konverguje: x n (n )! n! x n x n n n n x n 9 n n x n 4 n (, ) {0}, ) (, ) (, ) x n (, ) n x n n, n (x + ) n n ( x ) n (, ) (, ) ( ) n x(x + n) (, ) n n e nx (0, ) nx e nx 0, ) ln n x ( ) e, e
31 .4 Funkcionálne a mocninové rady V nasledujúcich úlohách určte polomer konvergencie mocninového radu: n xn (n ) (x )n x n n! n! x n 0 5 n n 5 n x n 5 n n xn n xn 5 ( ) n x n n n n (n + ) n xn (n + )(n + ) (x + n )n n k n! xn n! x n (n )! 0 n x n n 0 00 n x n n + 00 n n xn n n (x + ) n 0 (n )! n n x n e n n n! xn e n! (x )n e nn
32 NEKONEČNÉ RADY (n)! (n)! n n xn (n!) x n (n)! 4e 7 4 V nasledujúcich úlohách nájdite interval, na ktorom daný mocninový rad konverguje: n xn, (n ) (x )n 0, ) x n n! (, ) n! x n {0} n 5 n x n 5 n n n xn n xn ( ) n x n n n n (n + ) n xn ( 5, ) 5, ) 5, ) 5, ) (, ) (n + )(n + ) n (x + )n 4, n k n! xn n! x n (n )! 0 n n x n 00 n n + x n n n xn n n (x + ) n (, ) (, ) 0, ) 0 ) 00, 00 ( ), { }
33 .4 Funkcionálne a mocninové rady V nasledujúcich úlohách derivovaním alebo integrovaním vhodného radu nájdite súčet daného radu na vhodnom intervale:. (n + )x n ( x) n=0. (n + )(n + )x n ( x) n=0 n 5. 5 n xn (5 x) 4. (n + )x n + x ( x ) n=0 5. (x )n ln x + n ln (x ) n=0 V nasledujúcich úlohách pomocou základných mocninových radov určte Taylorov rad danej funkcie so stredom v bode a = 0: 6. f(x) = e x n=0 x n n n! 7. f(x) = e x n n! xn n=0 8. f(x) = e x ( ) n n n! xn n=0 x n+ 9. f(x) = x e x n! n=0 0. f(x) = xe x n n! xn+ n=0. f(x) = x e x ( ) n n. f(x) = xe x n=0 n=0 x n+ n n!. f(x) = x ( ) n e x n! n=0 4. f(x) = x e x x n+ n! n=0 5. f(x) = x e x ( ) n 6. f(x) = x ln( + x) n! ( ) n+ n=0 n n! xn+ x n+ x n+ x n+
34 4 NEKONEČNÉ RADY 7. f(x) = x ln( + x) 8. f(x) = ln( + x ) 9. f(x) = x ln( + x ) 40. f(x) = x sin x 40. f(x) = x cos x 4. f(x) = sin x V nasledujúcich úlohách nájdite Fourierov rad funkcie na danom intervale: ( ) n+ n ( ) n+ n ( ) n+ n=0 n=0 n=0 n x n+ x n x n+ ( ) n (n + )! xn+ ( ) n (n)! xn+ ( ) n (n + )! x4n+ ( ) n+ 4. f(x) = x, x, sin(nπx) nπ sin(nx) 4. f(x) = x, x 0, π π n f(x) = x, x π, π n ( )n+ sin(nx) 45. f(x) = x, x π, π ( ) n+ sin(nx) n 46. f(x) = x, x 0, π π 4 n sin(nx) { 0, pre x π, 0) 47. f(x) =, pre x (0, π + πn [ ( )n ] sin(nx) { π x, pre x π, 0) 48. f(x) = 0, pre x (0, π 49. f(x) = x, x π, π 50. f(x) = x, x π, π π 4 + [ ( ) n cos(nx) + ( )n πn n V nasledujúcich úlohách rozviňte funkciu f(x) do kosínusového radu: ] sin(nx) π + πn [( )n ] cos(nx) π + 4 n ( )n cos(nx)
35 .4 Funkcionálne a mocninové rady 5 5. f(x) = x, x 0, + (π n) [( )n ] cos(nπx) 5. f(x) = x, x 0, π π 4 + π n [( )n ] cos(nx) 5. f(x) = π 4 x, x 0, π π n [( )(n+) + ] cos(nx) 54. f(x) = x π, x 0, π + 4 n ( )n cos(nx) π 55. f(x) = x(π x), x 0, π 6 n [( )n+ ] cos(nx) 56. f(x) = x x, x 0, + 4 (π n) [( )n+ ] cos nπx V nasledujúcich úlohách rozviňte funkciu f(x) do sínusového radu: ( ) n+ 57. f(x) = x, x 0, sin(nπx) nπ 58. f(x) = x, x 0, π ( ) n+ sin(nx) n 59. f(x) = π 4 x, x 0, π n [( )n + ] sin(nx) [ ] 60. f(x) = x ( ) n, x 0, π π ( ) n sin(nx) π n n 4 6. f(x) = x(π x), x 0, π πn [ ( )n ] sin(nx) 6. f(x) = x x, x 0, 8 (π n) [( )(n+) + ] sin nπx
36 6 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH Diferenciálny počet funkcie viacerých premenných. Funkcia n premenných Definícia. n rozmerný euklidovský priestor E n je množina všetkých usporiadaných n tíc X = (x, x,..., x n ) reálnych čísel, pričom je definovaná vzdialenosť ρ ľubovoľných dvoch n tíc X = (x, x,..., x n ), Y = (y, y,..., y n ) vzťahom ρ = (x y ) + (x y ) + + (x n y n ). n ticu X = (x, x,..., x n ) reálnych čísel nazývame bodom priestoru E n a čísla x, x,..., x n súradnice tohto bodu. Definícia. Okolie bodu A resp. ɛ ové okolie O ɛ (A) bodu A E n je množina všetkých bodov X E n, ktorých vzdialenosť od bodu A je menšia ako ɛ. Platí O ɛ (A) = {X E n, ρ(a, X) < ɛ}. Definícia. Nech M E n. Bod A nazývame hromadným bodom množiny M, ak v každom okolí bodu A existuje aspoň jeden bod množiny M rôzny od bodu A. Poznámka: Hromadný bod množiny M nemusí patriť do množiny M. Definícia.4 Nech M E n. Funkcia n premenných je predpis f, ktorý každému X M priradí práve jedno y R. Píšeme y = f(x) alebo y = f(x, x,..., x n ). Definícia.5 Množinu M nazývame definičným oborom funkcie f a označujeme D(f). Príklad. Nájdime definičný obor funkcie f(x, y) = ln(9 x y ). Riešenie: Funkcia f(x, y) je definovaná pre body [x, y] spĺňajúce podmienku 9 x y > 0. Po úprave dostávame x + y < 9. Definičný obor funkcie f(x, y) je vnútro kruhu so stredom v bode [0, 0] a polomerom r = (pozri Obr. ). Definícia.6 Nech je funkcia f(x) definovaná v istom okolí bodu A = (a, a,..., a n ), ktorý je hromadným bodom jej definičného oboru D(f). Číslo b nazývame itou funkcie f(x) v bode A, ak pre každé ɛ > 0 existuje také δ > 0, že pre všetky X O δ (A), X A je f(x) O ɛ (b). Píšeme X A f(x) = b. Ak existuje f(x) = b, tak pre každú podmnožinu M D(f), ktorej hromadným bodom X A je bod A, platí f(x) = b a hovoríme, že b je ita funkcie f v bode A vzhľadom X A A M na množinu M.
37 . Parciálne derivácie funkcie n premenných 7 y x Obr. : Grafické zobrazenie definičného oboru funkcie ln(9 x y ) v rovine Poznámka: Ak pre dve množiny M D(f) a L D(f) sú ity X A X M rôzne, potom X A f(x) = b neexistuje. Základné vlastnosti ity funkcie viacerých premenných: f(x) a f(x) X A X L Nech funkcie f a g majú v bode A itu, f(x) = b R a g(x) = b R. Potom X A X A má v bode A itu aj funkcia: c f +c g, kde c, c sú ľubovoľné konštanty a platí X A (c f(x)+c g(x)) = c b +c b, f. g a platí X A f(x). g(x) = b b, f g f(x) a platí = b X A g(x) b, ak b 0. Príklad. Vypočítajme itu funkcie Riešenie: x y (x,y) (0,0) x +y (x,y) (0,0) x y x + y. je typu 0. Keďže ju nevieme ďalej upraviť, overíme si, či vôbec 0 daná ita existuje. Položíme y = kx, k 0 (sú to priamky prechádzajúce bodom (0, 0)). Po dosadení dostávame (x,y) (0,0) x y x + y = (x,y) (0,0) x kx x + (kx) = (x,y) (0,0) k + k = k + k. Daná ita závisi od k a teda pre rôzne hodnoty k, je hodnota ity rôzna. Z toho vyplýva, že x y (x,y) (0,0) x +y neexistuje.. Parciálne derivácie funkcie n premenných Definícia.7 Nech f je funkcia n premenných (x, x,..., x n ), n, definovaná na nejakom okolí bodu A = (a, a,..., a n ). Hovoríme, že funkcia f má v bode A konečnú parciálnu
38 8 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH deriváciu prvého rádu podľa premennej x i, ak existuje konečná ita f(a,..., a i, x i, a i+,..., a n ) f(a,..., a i, a i, a i+,..., a n ). x i a i x i a i Hodnotu tejto ity označujeme (A) x i alebo f x i (A). Ak je daná funkcia f n premenných, tak pri počítaní jej parciálnej derivácie podľa premennej x i postupujeme rovnako, ako pri počítaní derivácie funkcie jednej premennej. Teda použitím vzorcov pre derivovanie elementárnych funkcií a viet pre derivovanie. Pri derivovaní funkcie f podľa premennej x i budeme funkciu f považovať za funkciu jednej premennej a to premennej x i. Ostatné premenné v predpise funkcie f budeme považovať za konštanty. Parciálna derivácia funkcie f je opäť funkciou n premenných. Definícia.8 Nech f je funkcia n premenných, n, ktorá má na množine M parciálne derivácie prvého rádu x, x,..., x n. Parciálna derivácia druhého rádu podľa premených x i a x j je parciálna derivácia podľa premennej x i parciálnej derivácie funkcie f podľa premennej x j. Označujeme f x j x i a špeciálne, ak x i = x j, píšeme f. x i Poznámka: Ak sú parciálne derivácie f(a) x j x i = f(a) x i x j. f x j x i a f x i x j spojité v bode A D(f), tak platí Príklad. Určme parciálne derivácie funkcie f(x, y) = x y + y + x e 5y podľa jednotlivých premenných. Riešenie: Pri počítaní (x,y) premennú y považujeme za konštantu a funkciu f(x, y) derivujeme ako funkciu jednej premennej x, čím x dostaneme (x, y) x = 6xy + e 5y. Podobne pri počítaní (x,y) premennú x považujeme za konštantu a funkciu f(x, y) derivujeme y ako funkciu jednej premennej y, čím dostaneme (x, y) y = x + + 5x e 5y. Príklad.4 Nájdime parciálne derivácie funkcie f(x, y, z) = x + y z y z x premenných v bode A = (,, ). podľa jednotlivých Riešenie: Najprv nájdeme parciálne derivácie funkcie f(x, y, z) podľa jednotlivých premenných (x, y, z) x = y + z x, (x, y, z) y = x y + z, (x, y, z) z = y z x.
39 . Parciálne derivácie funkcie n premenných 9 Nakoniec dosadíme súradnice bodu A do jednotlivých parciálnych derivácií, čím dostaneme [ (A) = x y + z ] = x + = [, (A) = x y y + ] = z 4 + = 4, A (A) z = [ y z ] = =. x A A Príklad.5 Vypočítajme všetky parciálne derivácie druhého rádu funkcie f(x, y) = x y + y + xe 5y. Riešenie: Parciálne derivácie prvého rádu funkcie f(x, y) = x y + y + xe 5y sme vypočítali v Príklade.. Potom parciálne derivácie druhého rádu funkcie f(x, y) sú rovné f(x, y) x = x (6xy + e5y ) = 6y, f(x, y) x y = y (6xy + e5y ) = 6x + 5e 5y, f(x, y) y = y (x + + 5x e 5y ) = 5x e 5y, f(x, y) y x = x (x + + 5x e 5y ) = 6x + 5e 5y. Vidíme, že f(x, y) x y = f(x, y) y x... Parciálne derivácie zloženej funkcie Definícia.9 Nech funkcia f je definovaná na množine M E m a nech X = (x, x,..., x n ). Nech g (X), g (X),..., g m (X) je m funkcií n premenných, ktoré sú definované na množine P E n. Nech pre každé X P je bod (g (X), g (X),..., g m (X)) M. Potom funkciu F (X) = f(g (X), g (X),..., g m (X)) nazývame zloženou funkciou, ktorej definičný obor je množina P. Definícia.0 Nech X = (x, x,..., x n ) a F (X) = f(g (X), g (X),..., g m (X)) je zložená funkcia. Nech funkcie g i (X), i =,,..., m sú v bode A = (a, a,..., a n ) D(g i ) diferencovateľné. Nech funkcia f je v bode B = (g (A), g (A),..., g m (A)) D(f) diferencovateľná. Potom zložená funkcia F je diferencovateľná v bode A, pričom pre jej parciálne derivácie platí: F (A) x i = (B) g (A) g x i + (B) g (A) g x i + + (B) g m (A), i =,,... n. g m x i Príklad.6 Vypočítajme parciálne derivácie prvého rádu funkcie f(u, v) = uv, ak u = x 5y, v = xy + y.
40 40 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH Riešenie: Máme zloženú funkciu F (x, y) = f(u, v), pričom u = ϕ(x, y), v = ψ(x, y). Potom parciálne derivácie danej zloženej funkcie sú F x = u u x + v v x F y = u u y + v v y = v + u y = (xy + y) + y(x 5y), = v ( 5) + u (x + ) = 5(xy + y) + (x 5y)(x + ). Príklad.7 Vypočítajme parciálne derivácie prvého rádu funkcie f(u, v) = u v, ak u = ex, v = x. Riešenie: Máme zloženú funkciu F (x) = f(u, v), pričom u = ϕ(x), v = ψ(x). Potom parciálne derivácie danej zloženej funkcie sú df dx = du u dx + dv v dx = v ex + u ( v ) ( x ) = xe x + e x. Príklad.8 Vypočítajme parciálne derivácie prvého rádu funkcie f(u) = ln u, ak u = xy. Riešenie: Máme zloženú funkciu F (x, y) = f(u), pričom u = ϕ(x, y). Potom parciálne derivácie danej zloženej funkcie sú F x = df du u x = u y = xy y = x, F y = df u du y = u x = xy x = y... Dotyková rovina Definícia. Nech funkcia z = f(x, y) je spojitá a diferencovateľná v okolí bodu A = (x 0, y 0, z 0 ). Potom rovnica dotykovej roviny ρ ku grafu tejto funkcie v bode A je ρ : (x 0, y 0 ) x (x x 0 ) + (x 0, y 0 ) (y y 0 ) (z z 0 ) = 0 y a rovnica normály n ku grafu tejto funkcie v bode A je kde z 0 = f(x 0, y 0 ). n : x = x 0 + (x 0, y 0 ) t, x y = y 0 + (x 0, y 0 ) t, y z = z 0 t, t R.
41 . Lokálne extrémy funkcie n premenných 4 Príklad.9 Nájdime rovnicu dotykovej roviny ρ a normály n ku grafu funkcie danej rovnicou f(x, y) = arctg y x v bode A = (,,?). Riešenie: Z rovnice dotykovej roviny (x 0, y 0 ) x vyplýva, že potrebujeme určiť z 0 (x x 0 ) + (x 0, y 0 ) (y y 0 ) (z z 0 ) = 0 y z 0 = f(x 0, y 0 ) = f(, ) = arctg = π 4 a parciálne derivácie funkcie f(x, y) = arctg y x v bode A = (,, π 4 ) (x 0, y 0 ) x [ = ( y )] + ( y x ) x (x 0,y 0 ) Dosadením do rovnice dotykovej roviny dostávame =, (x 0, y 0 ) y ρ : (x ) + ( (y ) z π ) = 0, 4 [ ] = + ( y x ) x (x 0,y 0 ) =. po úprave ρ : x y + z π = 0. Zostáva nájsť rovnicu normály n ku grafu funkcie f(x, y) v bode A. Normála je priamka kolmá na dotykovú rovinu ρ a normálový vektor dotykovej roviny ρ je smerový vektor normály. Rovnica dotykovej roviny je ρ : x y + z π = 0, súradnice normálového vektora dotykovej roviny ρ sú (,, ). Potom parametrický tvar normály n ku grafu funkcie f(x, y) v bode A = (x 0, y 0, z 0 ) = (,, π) je 4 x = x 0 + t = + t, y = y 0 t = t, z = z 0 + t = π 4 + t, t R.. Lokálne extrémy funkcie n premenných Definícia. Hovoríme, že funkcia f(x) n premnenných má v bode A ostré lokálne maximum (lokálne maximum), ak pre každý bod X, X A z okolia bodu A platí f(x) < f(a) (f(x) f(a)). Definícia. Hovoríme, že funkcia f(x) n premnenných má v bode A ostré lokálne minimum (lokálne minimum), ak pre každý bod X, X A z okolia bodu A platí f(x) > f(a) (f(x) f(a)).
42 4 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH Definícia.4 Bod A, v ktorom parciálne derivácie prvého rádu sú rovné nule, nazývame stacionárny bod. Definícia.5 Stacionárne body a body, v ktorých parciálne derivácie neexistujú, sa nazývajú kritické body. Poznámka: Funkcia môže mať lokálny extrém len v kritickom bode. Nech bod A je stacionárnym bodom funkcie f(x) a nech v bode A je funkcia f(x) dva razy diferencovateľná. Potom: funkcia f(x) má v bode A ostré lokálne minimum (maximum), ak druhý diferenciál d f(a, X) > 0 (d f(a, X) < 0) pre každý bod X A, funkcia f(x) nemá v bode A lokálny extrém, ak existujú body X, X také, že d f(a, X ) a d f(a, X ) majú rôzne znamienka. Veta. (Postačujúca podmienka existencie extrému funkcie dvoch premenných) Nech bod A je stacionárnym bodom funkcie f(x, y) a nech má funkcia v okolí bodu A spojité parciálne derivácie prvého a druhého rádu. Nech determinant f(a) f(a) x = x y > 0. f(a) y x f(a) y Potom, ak = f(a) x 0, má funkcia f(x, y) v bode A lokálny extrém, a to lokálne minimum, ak súčasne platí = f(a) x > 0, lokálne maximum, ak súčasne platí = f(a) x < 0. Ak (A) < 0, tak nemá funkcia f(x, y) v bode A extrém (bod A sa nazýva sedlový bod). Poznámka: Ak (A) = 0, tak o lokálnom extréme pomocou uvedenej vety nevieme rozhodnúť. Je potrebné vyšetrovať funkciu f(x, y) v okolí stacionárneho bodu A inými metódami (napríklad testujeme funkčné hodnoty v okolí bodu A). Veta. (Postačujúca podmienka existencie extrému funkcie troch premenných) Nech bod A je stacionárnym bodom funkcie f(x, y, z) a nech má funkcia v okolí bodu A spojité parciálne derivácie prvého a druhého rádu. Nech determinant f(a) f(a) x = x y > 0. f(a) y x f(a) y Potom má funkcia f(x, y, z) v bode A lokálny extrém, a to
43 . Lokálne extrémy funkcie n premenných 4 lokálne minimum, ak súčasne platí = f(a) x f(a) f(a) x x y = f(a) f(a) y x f(a) z x y f(a) z y lokálne maximum, ak súčasne platí = f(a) x f(a) f(a) x x y = f(a) f(a) y x f(a) z x y f(a) z y > 0 a zároveň > 0, f(a) x z f(a) y z f(a) z < 0 a zároveň < 0. f(a) x z f(a) y z f(a) z Príklad.0 Nájdime lokálne extrémy funkcie f(x, y) = x + y + x y x 4. Riešenie: Najprv potrebujeme určiť stacionárne body. Nato musíme vypočítať parciálne derivácie prvého rádu funkcie f(x, y) (x, y) x = 6x + 6x, Stacionárne body nájdeme riešením sústavy rovníc (x, y) y = y. 6x + 6x = 0 y = 0. Stacionárne body sú A = (, ), B = (, ) C = (, ) a D = (, ). Využitím Vety. overíme extrémy v týchto stacionárnych bodoch. Vypočítame druhé parciálne derivácie f(x, y) x = x (6x + 6x ) = x + 6, f(x, y) x y = y (6x + 6x ) = 0, f(x, y) y = y (y ) = 6y, f(x, y) y x = x (y ) = 0. a určíme postupne hodnoty determinantov a v stacionárnych bodoch. 8 0 Pre stacionárny bod A platí (A) = 0 6 = 08 > 0 (A) = 8 > 0 v bode A je lokálne minimum. 8 0 Pre stacionárny bod B platí (B) = 0 6 = 08 < 0 (B) = 8 0 v bode B nie je extrém a bod B je sedlový bod. 8 0 Pre stacionárny bod C platí (C) = 0 6 = 08 < 0 (B) = 8 0
44 44 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH v bode C nie je extrém a bod C je sedlový bod. 8 0 Pre stacionárny bod D platí (D) = 0 6 v bode D je lokálne maximum. = 08 > 0 (D) = 8 < 0.4 Viazané extrémy funkcie dvoch premenných Definícia.6 Nech funkcia f(x, y) je definovaná na množine M a množinu L nech tvoria všetky body z M, ktoré vyhovujú rovnici g(x, y) = 0. Lokálne extrémy funkcie f(x, y) na množine L nazývame viazanými lokálnymi extrémami a podmienku g(x, y) = 0, ktorá určuje množinu L, nazývame väzbou. Pri hľadaní extrémov môžu nastať dva prípady: ak sa z väzby g(x, y) = 0 dá jednoznačne vyjadriť niektorá premenná, dosadíme ju do funkcie f(x, y), dostaneme funkciu jednej premennej a viazaný extrém danej funkcie hľadáme ako lokálny extrém funkcie jednej premennej, ak sa z väzby g(x, y) = 0 nedá jednoznačne vyjadriť žiadna premenná, zostrojíme Lagrangeovu funkciu L(x, y) = f(x, y) + λg(x, y), λ R. Vypočítame jej parciálne derivácie podľa premenných x a y L x = x + λ g x, L y = y + λ g y a stacionárne body Lagrangeovej funkcie L(x, y) nájdeme riešením sústavy rovníc x + λ g x = 0 y + λ g y = 0 g(x, y) = 0. Závery pre existenciu viazaného lokálneho extrému sú rovnaké ako pri lokálnych extrémoch, avšak ak Lagrangeova funkcia nemá lokálny extrém, o existencii viazaného lokálneho extrému funkcie f(x, y) nevieme povedať nič. V takom prípade musíme hľadať viazaný extrém iným spôsobom. Poznámka: Ak Lagrangeova funkcia L(x, y) má extrém, tak tento extrém je extrémom funkcie f(x, y) (naopak to neplatí). Príklad. Nájdime viazané extrémy funkcie f(x, y) = e xy, ak x + y =.
45 .4 Viazané extrémy funkcie dvoch premenných 45 Riešenie: Z funkcie g(x, y) = 0, t. j. x+y = 0, predstavujúcej väzbu môžeme jednoznačne vyjadriť ľubovoľnú z dvoch premenných, napr. y = x. Takto vyjadrené y dosadíme do funkcie f(x, y) a dostaneme funkciu jednej premennej f(x) = e x( x) = e x x. Vypočítame deriváciu prvého rádu funkcie f(x) f (x) = ( x)e x x a položíme ju rovnú nule, čím dostávame rovnicu ( x)e x x = 0. Riešením danej rovnice dostaneme stacionárny bod A = (, ). Potom určíme hodnotu derivácie druhého rádu funkcie f(x) v stacionárnom bode A f (A) = [( x)e x x] [ = (4x 8x + )e x x] = e < 0. A A Funkcia f(x, y) = e xy s väzbou x + y = má v bode A lokálne maximum a f(a) = e. Príklad. Nájdime viazané extrémy funkcie f(x, y) = x + y, ak x + y = 5. Riešenie: Keďže z funkcie g(x, y) = 0, t. j. x + y 5 = 0, predstavujúcej väzbu nemôžeme jednoznačne vyjadriť žiadnu z dvoch premenných, zostrojíme Lagrangeovu funkciu L(x, y) = x + y + λ(x + y 5), λ R a hľadáme jej extrémy. Najprv vypočítame parciálne derivácie prvého rádu Lagrangeovej funkcie L x = + xλ, L y = + yλ. Stacionárne body funkcie L(x, y) nájdeme riešením sústavy rovníc + xλ = 0 + yλ = 0 g(x, y) = x + y 5 = 0. Ak z prvej rovnice vyjadríme x, z druhej y a dosadíme ich do tretej rovnice, tak dostaneme rovnicu 4λ + λ 5 = 0. Riešením danej rovnice dostaneme λ =, λ = a určíme stacionárne body v závislosti na λ, λ. Pre λ = je A = (, ), pre λ = je B = (, ). Ďalej postupujeme podobne ako v Príklade.0. Vypočítame parciálne derivácie druhého rádu a určíme ich hodnoty v stacionárnych bodoch. Platí
46 46 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH L(x, y) x = λ, L(x, y) y x = 0, L(x, y) L(x, y) = λ, = 0. y x y 0 Pre stacionárny bod A platí (A) = 0 = > 0 (A) = > 0 v bode A viazané lokálne minimum a f(a) = 5. 0 Pre stacionárny bod B platí (B) = 0 = > 0 (B) = > 0 v bode B je viazané lokálne maximum a f(b) = 5. Neriešené úlohy: V nasledujúcich úlohách určte definičný obor funkcie f(x, y) a znázornite ho graficky:. f(x, y) = x + y x y x. f(x, y) = x + 7 ex y. f(x, y) = x + y x +. f(x, y) = x + y x y. f(x, y) = xy x + y 4. f(x, y) = y xy x y 4. f(x, y) = ln x x y + x + y 5. f(x, y) = e xy x 6 + xy x 4 5. f(x, y) = y x y + ex+y 6. f(x, y) = ln ( + xy) + e x y 6. f(x, y) = + x y 7. f(x, y) = ln (xy 4) + y x + y 5 x + 7. f(x, y) = y x f(x, y) = x ln ( x y ) 8. f(x, y) = y x 9. f(x, y) = ln (x + e y ) + y x + 9. f(x, y) = 4 y x 0. f(x, y) = x ln y y ln x + xy 0. f(x, y) = 6 x y. f(x, y) = x+y + x y ln(x y). f(x, y) = x + y + x + 5 V nasledujúcich úlohách vypočítajte itu danej funkcie:. x + y (x,y) (0,4). (x,y) (4, ) 4. (x,y) (0,0) 5. (x,y) (0,) x y 9 x y 6 x + y 4 x y x + (y ) + x + (y ) 4
47 .4 Viazané extrémy funkcie dvoch premenných arcsin (x,y) (0, ) x y x sin(xy) 7. (x,y) (,0) ( xy ) sin x 8. (x,y) (0, ) 9. (x,y) (4,0) x tg (xy) y + y 0. arctgy neexistuje (x,y) (0,0) x xy. neexistuje (x,y) (0,0) x + y x + y. neexistuje (x,y) (0,0) x y x + y. neexistuje (x,y) (0,0) y x y 4. neexistuje (x,y) (0,0) x + y xy x y + 5. neexistuje (x,y) (,) x + y x 4y + 5 xy x + y 6. neexistuje (x,y) (,) (x + ) + (y ) x 7. neexistuje (x,y,z) (0,0,0) x + y + z (x z + ) 8. neexistuje (x,y,z) (,0,0) (x + ) + y + z V nasledujúcich úlohách určte parciálne derivácie funkcie f(x, y) podľa jednotlivých premenných: 9. f(x, y) = x + y 5xy 40. f(x, y) = ln(y 4x + 8) 4. f(x, y) = arctg x + y 4. f(x, y) = (x + 5y) sin x 4. f(x, y) = x + y x 44. f(x, y) = x y x + y 45. f(x, y) = 9 y x x + 7 ex y x = x 5y, x = 4 y 4x + 8, y = y = y 5x π 4 y y 4x + 8 x = 8x 8 + (x + y ), y = 8y 8 + (x + y ) = sin x + (x + 5y) cos x x = 5 sin x y x = y + ( x), y = x x = 4xy (x + y ), y = 4x y (x + y ) x = y x 4x (x + 7) ex y
48 48 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH 46. f(x, y) = x + y x f(x, y) = ln x x y + x + y 48. f(x, y) = y x y + ex+y 49. f(x, y) = + x y x + y f(x, y) = y x f(x, y) = y x y = x e x (y ) x = x (x ) y (x + ), y = x + x = y ln x x 4x (x y) (x + y ) y = 5. f(x, y) = 4 y x x = 5. f(x, y) = 6 x y x = 54. f(x, y) = x + y + x f(x, y) = y xy x y 56. f(x, y) = e xy x f(x, y) = ln ( + xy) + e x y x = 58. f(x, y) = ln (xy 4) + y x f(x, y) = x ln ( x y ) ln x (x y) 4y (x + y ) x(y ) = x (x y ) + ex+y y = x y + 6y + e x+y (x y ) x = x + y x + xy 5 (x + y 5) y = yx + 8y xy (x + y 5) x = y x + 5, y = y x + 5 x = y x, y = y y x x 4 (y x ), y = y 4 (y x ) x 6 x y, y = y 6 x y x = x x + y + x x + 5 y = y x + y x = y xy (x y) x y y = xy + x y 4x y (x y) x y x = exy (yx 6y x) (x 6) x 6, y = xexy x 6 y + xy + ex y, y = y (x + ), y = x = y xy 4 x = ln ( x y ) y = xy x y x + xy ex y x x y x xy 4 + x +
49 .4 Viazané extrémy funkcie dvoch premenných f(x, y) = ln (x + e y ) + y x + 6. f(x, y) = x ln y y ln x + xy 6. f(x, y) = x+y x y + ln(x y) x = x x + e y y x + y = ey x + e + y y x + x = ln y y x + y xy y = ln x + x y + x xy x = y x y (x y) x + y + x x y y = x x y (x y) x + y x y 6. f(x, y) = x + y x y 64. f(x, y) = xy x + y x = y = x = y = x x + y 4 y x + y 4 x 9 x y y 9 x y xy + y 4y (x + y ) x + y 65. f(x, y) = e x y + x y x = y e x y + yx y, 66. f(x, y) = xye x+y x = yex+y ( + x), 67. f(x, y) = xe x y x = ( + x)ex y, 68. f(x, y) = ye x +y x xy + x 4x (x + y ) x + y y = x y e x y + x y ln x +y = xyex, 69. f(x, y) = (x y )e xy x = ( + xy y4 )e xy 70. f(x, y) = cos(x y) x + y 7. f(x, y) = cotg x y x + y 7. f(x, y) = (x + y) sin xy y = xex+y ( + y) y = xex y y = ( + y x +y )e y = ( y + x xy )e xy (x + y) sin(x y) cos(x y) = x (x + y) (x + y) sin(x y) cos(x y) = y (x + y) x = y (x + y) sin x y, y = x (x + y) x+y sin x y x+y x = x sin xy + (yx + y ) cos xy y = sin xy + (x + yx) cos xy
50 50 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH 7. f(x, y) = x sin y + ln tg x y x = sin y x sin y + y sin x cos x y y y = x cos y x sin y x y sin x cos x y y V nasledujúcich úlohách určte parciálne derivácie danej funkcie podľa jednotlivých premenných v bode A: 74. f(x, y) = arctg x y, A = (0, ) (A) (A) =, = 0 x y 75. f(x, y) = x y + e xy (A), A = (, ) = + e (A), = + e x y 76. f(x, y) = e sin y (A) (A) x, A = (, 0) = 0, = x y 77. f(x, y) = 4 y x, A = (0, ) x = 0, y = 78. f(x, y) = (A) 6 x y, A = (, ) = x, (A) = y 79. f(x, y) = ln ( + xy) + e x y (A), A = (, ) = x 4, (A) = 5 y f(x, y) = ln x x y + (A), A = (, ) = x + y x, (A) = y ( π 8. f(x, y) = y sin(x y ), A =, π ) (A) = π x 4, (A) = π y 4 8. f(x, y, z) = y cos x + z cos y + x sin z, ( A = 0, π, π ) 8. f(x, y, z) = ln(x + y + z ), A = (,, ) (A) = x (A) x, (A) y = 7, (A) y = π, (A) z = 7, (A) z = 7 = 0 V nasledujúcich úlohách určte parciálne derivácie zloženej funkcie podľa jednotlivých premenných: df 84. f(x, y) = x y, x = t, y = t + dt = 85. f(x, y) = x y, x = e t, y = e 5t df dt = 4et + 5e 5t 86. f(x, y) = x y, x = ln t, y = df t dt = t + t 87. f(x, y) = df xy, x = t, y = t + dt = t + t + t 88. f(x, y) = xy, x = e t, y = e 5t df dt = et + e t e t e t 89. f(x, y) = xy, x = ln t, y = df t dt = ln t t ln t t
51 .4 Viazané extrémy funkcie dvoch premenných f(x, y) = y ln x, x = t, y = t + df dt = ln t + t + t 9. f(x, y) = y ln x, x = e t, y = e 5t df dt = e 5t ( 0t + ) 9. f(x, y) = y ln x, x = ln t, y = t df dt = ln t ln(ln t) t ln t 9. f(x, y) = x y, x = ln t, y = + e t df dt = + e t t + et ln t + e t 94. f(x, y) = arcsin (x y), x = t, y = 4t df dt = t (t 4t ) 95. f(x, y) = x y y x, x = u + v, y = u v u = u u + 4u + v v v u v v = u + u + u v v + u v 96. f(x, y) = x y y x, x = e u, y = e v u = eu+ v e u+ v 97. f(x, y) = x y y x, x = ln(u + v), y = u + v v = eu+ v + e u+ v u = v = ln(u + v) ln (u + v) ln(u + v) (u + v) (u + v) x 98. f(x, y) = y, x = (u + v), y = v u x 99. f(x, y) = y, x = e4u v, y = uv 00. f(x, y) = x y, x = u v, y = u + v u = v (v u), v = u = eu v (u ) uv v = eu v (v + ) u v u = v = 0. f(x, y) = x ln y, x = u v, y = u v u = u v 0. f(x, y) = x, x = u v, y = v + u y u (v u) v (u + v) u v u+v u (u + v) u v u+v ( ln(u v) + u ) u v ( ) ln(u v) + v u v v = u v u v = (u v)(u + v) (u + v) = (v u)(9u + v) (u + v)
52 5 DIFERENCIÁLNY POČET FUNKCIE VIACERÝCH PREMENNÝCH V nasledujúcich úlohách nájdite rovnicu dotykovej roviny ρ a normály n ku grafu funkcie f(x, y) v dotykovom bode A: 0. f(x, y) = (y x ), A = (,,?) ρ : 4x 4y z + 4 = 0 n : x = + 4t, y = 4t, z = 4 t, t R 04. f(x, y) = 4 x y, A = (,,?) ρ : x + y + z 4 = 0 n : x = + t, y = + t, z = + t, t R 05. f(x, y) = x 4y, A = (,,?) ρ : 8x 8y z 4 = f(x, y) = x + y, A = (, 4,?) ρ : x + 4y 5z = f(x, y) = sin x, A = (π,,?) ρ : x πy + z = 0 y n : x = + 8t, y = 8t, z = 4 t, t R n : x = + t, y = 4 + 4t, z = 5 5t, t R ( π ) 08. f(x, y) = e y sin x, A = 4, 0,? n : x = π + t, y = πt, z = t, t R ρ : x + y z + ( π ) = 0 4 n: x = π 4 + t, y = t, z = t, t R V nasledujúcich úlohách nájdite rovnicu dotykovej roviny ρ ku grafu danej funkcie, pričom dotyková rovina je rovnobežná s danou rovinou σ: 09. f(x, y) = 4x + y, σ : x + y z + = 0 ρ : 8x + 8y 4z 5 = 0 0. f(x, y) = 4 x y, σ : x + y z = 0 ρ : x + y z + 6 = 0. f(x, y) = x + y, σ : x + y + z = ρ : 6(x + ) + (y + 4 ) + ( z 45 6) = 0. f(x, y) = + (x ) + y, σ : z = 0 ρ : z = 0 V nasledujúcich úlohách nájdite lokálne extrémy funkcie f(x, y):. f(x, y) = 4 x y lok. max. v (0, 0) 4. f(x, y) = 0 x y lok. max. v (0, 0) 5. f(x, y) = x + y lok. min. v (0, 0) 6. f(x, y) = x + y + lok. min. v (0, 0) 7. f(x, y) = x + y x + lok. min. v (, 0) 8. f(x, y) = x + y + 4y + lok. min. v (0, ) 9. f(x, y) = 4 x y x lok. max. v (, 0) 0. f(x, y) = x + y 4x + 4y + 8 lok. min. v (, ). f(x, y) = x y + x y nemá extrém. f(x, y) = x y + 6x + y lok. max. v (, ) f(x, y) = (x ) + 4y lok. min. v (, 0)
Matematika 2 - cast: Funkcia viac premenných
 Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
Matematika 2 časť: Funkcia viac premenných RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Spojitosť
Priebeh funkcie
 Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
A 1
 Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
Matematika A :: Test na skúške (ukážka) :: 05 Daná je funkcia g : y 5 arccos a) Zistite oblasť definície funkcie b) vyjadrite inverznú funkciu g Zistite rovnice asymptot (so smernicou bez smernice) grafu
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) Matematická analýza IV (ÚMV/MAN2d/10) RNDr. Lenka Halčinová, PhD.
 III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
1 Priebeµzné písomné zadanie µc.1. Príklady je potrebné vypoµcíta t, napísa t, a odovzda t, na kontrolu na nasledujúcej konzultácii. Nasledujúce integ
 Priebeµzné písomné zadanie µc.. Príklady je potrebné vypoµcíta t, napísa t, a odovzda t, na kontrolu na nasledujúcej konzultácii. Nasledujúce integrály vypoµcítajte pomocou základných pravidiel derivovania.
Priebeµzné písomné zadanie µc.. Príklady je potrebné vypoµcíta t, napísa t, a odovzda t, na kontrolu na nasledujúcej konzultácii. Nasledujúce integrály vypoµcítajte pomocou základných pravidiel derivovania.
4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia p
 4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia pre funkcie viacerých premenných je univerzálna metóda,
4. Pravidlo ret azenia. Často sa stretávame so skupinami premenných, ktoré zložitým spôsobom závisia od iných skupín premenných. Pravidlo ret azenia pre funkcie viacerých premenných je univerzálna metóda,
Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1
 Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1 A Pomocou Charpitovej metódy vyriešte rovnicu. x u x + y u y = u u x y u 2 = xy u u x y 3. u 2 y = u y u 4. u 2 x = u x u u x = B.
Jozef Kiseľák Sada úloh na precvičenie VIII. 15. máj 2014 A. (a) (b) 1 A Pomocou Charpitovej metódy vyriešte rovnicu. x u x + y u y = u u x y u 2 = xy u u x y 3. u 2 y = u y u 4. u 2 x = u x u u x = B.
1. KOMPLEXNÉ ČÍSLA 1. Nájdite výsledok operácie v tvare x+yi, kde x, y R. a i (5 2i)(4 i) b. i(1 + i)(1 i)(1 + 2i)(1 2i) (1 7i) c. (2+3i) a+bi d
 KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom
 2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x x x 1 s.t. x 1 80 x 1 + x Pre riešenie úlohy vykonáme nasledujúce kroky
 Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x 2 1 + x2 2 + 60x 1 s.t. x 1 80 x 1 + x 2 120 Pre riešenie úlohy vykonáme nasledujúce kroky: 1. Najskôr upravíme ohraničenia do tvaru a následne
Cvičenie 9 Riešené príklady 1. Príklad min f(x 1, x 2 ) = x 2 1 + x2 2 + 60x 1 s.t. x 1 80 x 1 + x 2 120 Pre riešenie úlohy vykonáme nasledujúce kroky: 1. Najskôr upravíme ohraničenia do tvaru a následne
Teória pravdepodobnosti Zákony velkých císel
 10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
10. Zákony veľkých čísel Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. apríla 2014 1 Zákony veľkých čísel 2 Centrálna limitná veta Zákony veľkých čísel Motivácia
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1.2 Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru
 8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
Informačná a modelová podpora pre kvantifikáciu prvkov daňovej sústavy SR
 Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Microsoft Word - 6 Výrazy a vzorce.doc
 6 téma: Výrazy a vzorce I Úlohy na úvod 1 1 Zistite definičný obor výrazu V = 4 Riešte sústavu 15 = 6a + b, = 4a c, 1 = 4a + b 16c Rozložte na súčin výrazy a) b 4 a 18, b) c 5cd 10c d +, c) 6 1 s + z 4
6 téma: Výrazy a vzorce I Úlohy na úvod 1 1 Zistite definičný obor výrazu V = 4 Riešte sústavu 15 = 6a + b, = 4a c, 1 = 4a + b 16c Rozložte na súčin výrazy a) b 4 a 18, b) c 5cd 10c d +, c) 6 1 s + z 4
Operačná analýza 2
 Súradnicové sústavy a zobrazenia Súradnicové sústavy v rovine (E 2 ) 1. Karteziánska súradnicová sústava najpoužívanejšia súradnicová sústava; určená začiatkom O, kolmými osami x, y a rovnakými jednotkami
Súradnicové sústavy a zobrazenia Súradnicové sústavy v rovine (E 2 ) 1. Karteziánska súradnicová sústava najpoužívanejšia súradnicová sústava; určená začiatkom O, kolmými osami x, y a rovnakými jednotkami
Operačná analýza 2
 Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Microsoft Word - mpicv11.doc
 1. Vypočítajte obsah plochy ohraničenej súradnicovými osami a grafom funkcie y = x. a) vypočítame priesečníky grafu so súradnicovými osami x=... y = = y =... = x... x= priesečníku grafu funkcie so ; a
1. Vypočítajte obsah plochy ohraničenej súradnicovými osami a grafom funkcie y = x. a) vypočítame priesečníky grafu so súradnicovými osami x=... y = = y =... = x... x= priesečníku grafu funkcie so ; a
Slide 1
 Diferenciálne rovnice Základný jazyk fyziky Motivácia Typická úloha fyziky hľadanie časových priebehov veličín, ktoré spĺňajú daný fyzikálny zákon. Určte trajektóriu telesa rt ( )???? padajúceho v gravitačnom
Diferenciálne rovnice Základný jazyk fyziky Motivácia Typická úloha fyziky hľadanie časových priebehov veličín, ktoré spĺňajú daný fyzikálny zákon. Určte trajektóriu telesa rt ( )???? padajúceho v gravitačnom
Funkcie viac premenných
 Funkcie viac premenných January 21, 215 Regulárne zobrazenia Nech je zobrazenie X = Φ(T) dané rovnicami: x 1 = ϕ 1 (t 1, t 2,, t n), x 2 = ϕ 2 (t 1, t 2,, t n), x n = ϕ n(t 1, t 2,, t n), a ak majú funkcie
Funkcie viac premenných January 21, 215 Regulárne zobrazenia Nech je zobrazenie X = Φ(T) dané rovnicami: x 1 = ϕ 1 (t 1, t 2,, t n), x 2 = ϕ 2 (t 1, t 2,, t n), x n = ϕ n(t 1, t 2,, t n), a ak majú funkcie
Ďalšie vlastnosti goniometrických funkcií
 Ďalšie vlastnosti goniometrických funkcií Na obrázku máme bod B na jednotkovej kružnici, a rovnobežne s y-ovou osou bodom B vznikol pravouhlý trojuholník. Jeho prepona je polomer kružnice má veľkosť 1,
Ďalšie vlastnosti goniometrických funkcií Na obrázku máme bod B na jednotkovej kružnici, a rovnobežne s y-ovou osou bodom B vznikol pravouhlý trojuholník. Jeho prepona je polomer kružnice má veľkosť 1,
Microsoft Word - Final_test_2008.doc
 Záverečná písomka z Matematiky pre kog. vedu konaná dňa 3. 1. 008 Príklad 1. Odpovedzte na otázky z výrokovej logiky: (a Ako je definovaná formula (b Aký je rozdiel medzi tautológiou a splniteľnou formulou
Záverečná písomka z Matematiky pre kog. vedu konaná dňa 3. 1. 008 Príklad 1. Odpovedzte na otázky z výrokovej logiky: (a Ako je definovaná formula (b Aký je rozdiel medzi tautológiou a splniteľnou formulou
S rok 2 roky t = 4 1 rok MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku informatiku Monika Molnárová Košice 2018
 S 230 280 270 0 1 2 3 4 5 1 rok 2 roky t = 4 1 rok MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku informatiku Monika Molnárová Košice 2018 MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku
S 230 280 270 0 1 2 3 4 5 1 rok 2 roky t = 4 1 rok MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku informatiku Monika Molnárová Košice 2018 MATEMATIKA I A REPETITÓRIUM Z MATEMATIKY pre Hospodársku
9.1 MOMENTY ZOTRVACNOSTI \(KVADRATICKÉ MOMENTY\) A DEVIACNÝ MOMENT PRIEREZU
 Učebný cieľ kapitoly Po preštudovaní tejto kapitoly by ste mali ovládať: Charakteristiku kvadratických momentov prierezových plôch. Ako je definovaný kvadraticky moment plochy k osi a k pólu. Ako je definovaný
Učebný cieľ kapitoly Po preštudovaní tejto kapitoly by ste mali ovládať: Charakteristiku kvadratických momentov prierezových plôch. Ako je definovaný kvadraticky moment plochy k osi a k pólu. Ako je definovaný
Axióma výberu
 Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Axióma výberu 29. septembra 2012 Axióma výberu Axióma VIII (Axióma výberu) ( S)[( A S)(A ) ( A S)( B S)(A B A B = ) ( V )( A S)( x)(v A = {x})] Pre každý systém neprázdnych po dvoch disjunktných množín
Microsoft Word - Transparencies03.doc
 3. prednáška Teória množín II relácie o operácie nad reláciami o rovnosť o usporiadanosť funkcie o zložená funkcia o inverzná funkcia. Verzia: 20. 3. 2006 Priesvitka: 1 Relácie Definícia. Nech X a Y sú
3. prednáška Teória množín II relácie o operácie nad reláciami o rovnosť o usporiadanosť funkcie o zložená funkcia o inverzná funkcia. Verzia: 20. 3. 2006 Priesvitka: 1 Relácie Definícia. Nech X a Y sú
Informačné technológie
 Informačné technológie Piatok 15.11. 2013 Matúš Péči Barbora Zahradníková Soňa Duchovičová Matúš Gramlička Začiatok/Koniec Z K Vstup/Výstup A, B Načítanie vstupných premenných A, B resp. výstup výstupných
Informačné technológie Piatok 15.11. 2013 Matúš Péči Barbora Zahradníková Soňa Duchovičová Matúš Gramlička Začiatok/Koniec Z K Vstup/Výstup A, B Načítanie vstupných premenných A, B resp. výstup výstupných
Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1
 Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1 Metódy riešenia úloh nelineárneho programovania využívajúce Lagrangeovu funkciu 2 Veta: Bod ˆx je optimálne riešenie úlohy (U3)
Neineárne programovanie zimný semester 2018/19 M. Trnovská, KAMŠ, FMFI UK 1 Metódy riešenia úloh nelineárneho programovania využívajúce Lagrangeovu funkciu 2 Veta: Bod ˆx je optimálne riešenie úlohy (U3)
Slide 1
 SÚSTAVA TRANSF. VZŤAHY Plošné, objemové element Polárna Clindrická rcos rsin rcos r sin z z ds rddr dv rddrdz rcossin Sférická r sin sin dv r sin drd d z rcos Viacrozmerné integrál vo fzike Výpočet poloh
SÚSTAVA TRANSF. VZŤAHY Plošné, objemové element Polárna Clindrická rcos rsin rcos r sin z z ds rddr dv rddrdz rcossin Sférická r sin sin dv r sin drd d z rcos Viacrozmerné integrál vo fzike Výpočet poloh
Základné stochastické procesy vo financiách
 Technická Univerzita v Košiciach Ekonomická fakulta 20. Január 2012 základné charakteristiky zmena hodnoty W t simulácia WIENEROV PROCES základné charakteristiky základné charakteristiky zmena hodnoty
Technická Univerzita v Košiciach Ekonomická fakulta 20. Január 2012 základné charakteristiky zmena hodnoty W t simulácia WIENEROV PROCES základné charakteristiky základné charakteristiky zmena hodnoty
Microsoft Word - skripta3b.doc
 6. Vlastnosti binárnych relácií V tejto časti sa budeme venovať šiestim vlastnostiam binárnych relácií. Najprv si uvedieme ich definíciu. Reláciu R definovanú v množine M nazývame: a ) reflexívnou, ak
6. Vlastnosti binárnych relácií V tejto časti sa budeme venovať šiestim vlastnostiam binárnych relácií. Najprv si uvedieme ich definíciu. Reláciu R definovanú v množine M nazývame: a ) reflexívnou, ak
Microsoft Word - Zaver.pisomka_januar2010.doc
 Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Pokrocilé programovanie XI - Diagonalizácia matíc
 Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy
 Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy) alebo analyticky (výpočet súradníc bodov elipsy).
Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy) alebo analyticky (výpočet súradníc bodov elipsy).
O možnosti riešenia deformácie zemského povrchu z pohladu metódy konecných prvkov konference pro studenty matematiky
 O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
O možnosti riešenia deformácie zemského povrchu z pohľadu metódy konečných prvkov 19. konference pro studenty matematiky Michal Eliaš ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Katedra matematiky 7. 9. 6. 2011
Snímka 1
 Fyzika - prednáška 8 Ciele 3. Kmity 3.1 Netlmený harmonický kmitavý pohyb 3. Tlmený harmonický kmitavý pohyb Zopakujte si Výchylka netlmeného harmonického kmitavého pohybu je x = Asin (ω 0 t + φ 0 ) Mechanická
Fyzika - prednáška 8 Ciele 3. Kmity 3.1 Netlmený harmonický kmitavý pohyb 3. Tlmený harmonický kmitavý pohyb Zopakujte si Výchylka netlmeného harmonického kmitavého pohybu je x = Asin (ω 0 t + φ 0 ) Mechanická
Microsoft Word - Algoritmy a informatika-priesvitky02.doc
 3. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi základné formálne prostriedky
3. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi základné formálne prostriedky
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/ ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných r
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 009/010 59. ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných reálnych čísel, ktoré sú riešením sústavy rovníc a b c
SK MATEMATICKÁOLYMPIÁDA skmo.sk 009/010 59. ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných reálnych čísel, ktoré sú riešením sústavy rovníc a b c
Microsoft Word - FRI”U M 2005 forma B k¾úè.doc
 Fakulta riadenia a informatik Žilinskej univerzit ( ) ( 6 ) 6 = 3 () 8 (D) 8 m Závislosť hmotnosti m častice od jej rýchlosti v je vjadrená vzťahom m =, kde m je v c pokojová hmotnosť častice, c je rýchlosť
Fakulta riadenia a informatik Žilinskej univerzit ( ) ( 6 ) 6 = 3 () 8 (D) 8 m Závislosť hmotnosti m častice od jej rýchlosti v je vjadrená vzťahom m =, kde m je v c pokojová hmotnosť častice, c je rýchlosť
VZTAH STUDENTŮ VŠ K DISCIPLÍNÁM TEORETICKÉ INFORMATIKY
 5. vedecká konferencia doktorandov a mladých vedeckých pracovníkov LIMITA A DERIVÁCIA FUNKCIE UKÁŽKA KVANTITATÍVNEHO VÝSKUMU Ján Gunčaga The present paper is devoted to a qualitative research related to
5. vedecká konferencia doktorandov a mladých vedeckých pracovníkov LIMITA A DERIVÁCIA FUNKCIE UKÁŽKA KVANTITATÍVNEHO VÝSKUMU Ján Gunčaga The present paper is devoted to a qualitative research related to
Matematický model činnosti sekvenčného obvodu 7 MATEMATICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčnéh
 7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
Model tesnej väzby (TBH) Peter Markoš, KF FEI STU April 21, 2008 Typeset by FoilTEX
 Model tesnej väzby (TBH) Peter Markoš, KF FEI STU April 21, 28 Typeset by FoilTEX Obsah 1. TBH: definícia: elektrónový, elektromagnetický 2. Disperzné vzt ahy 3. Spektrum, okrajové podmienky 4. TBH vs.
Model tesnej väzby (TBH) Peter Markoš, KF FEI STU April 21, 28 Typeset by FoilTEX Obsah 1. TBH: definícia: elektrónový, elektromagnetický 2. Disperzné vzt ahy 3. Spektrum, okrajové podmienky 4. TBH vs.
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 1. 3. marca 2006 2. 10. marca 2006 c RNDr. Monika Molnárová, PhD. Obsah 1 Aritmetické vektory a matice 4 1.1 Aritmetické vektory........................
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 1. 3. marca 2006 2. 10. marca 2006 c RNDr. Monika Molnárová, PhD. Obsah 1 Aritmetické vektory a matice 4 1.1 Aritmetické vektory........................
SK MATEMATICKÁOLYMPIÁDA skmo.sk 63. ročník Matematickej olympiády 2013/2014 Riešenia úloh česko-poľsko-slovenského stretnutia 1. Dokážte, že kladné re
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 63. ročník Matematickej olympiády 2013/2014 Riešenia úloh česko-poľsko-slovenského stretnutia 1. Dokážte, že kladné reálne čísla a, b, c spĺňajú rovnicu a 4 + b 4 + c 4
SK MATEMATICKÁOLYMPIÁDA skmo.sk 63. ročník Matematickej olympiády 2013/2014 Riešenia úloh česko-poľsko-slovenského stretnutia 1. Dokážte, že kladné reálne čísla a, b, c spĺňajú rovnicu a 4 + b 4 + c 4
9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty 1. Systém lineárnych rovníc Systém
 9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty. Systém lineárnych rovníc Systém lineárnych rovníc, ktorý obsahuje m rovníc o n neznámych
9. kapitola Maticová algebra II systém lineárnych rovníc, Frobeniova veta, Gaussova eliminačná metóda, determinanty. Systém lineárnych rovníc Systém lineárnych rovníc, ktorý obsahuje m rovníc o n neznámych
Prenosový kanál a jeho kapacita
 Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Preco kocka stací? - o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, ked sú velké
 o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
Pocítacové modelovanie - Šírenie vln v nehomogénnom prostredí - FDTD
 Počítačové modelovanie Šírenie vĺn v nehomogénnom prostredí - FDTD Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2016/2017 Úvod Hľadáme riešenia časovo závislej parciálnej diferenciálnej
Počítačové modelovanie Šírenie vĺn v nehomogénnom prostredí - FDTD Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2016/2017 Úvod Hľadáme riešenia časovo závislej parciálnej diferenciálnej
Seriál XXXII.II Mechanika, FYKOS
 Seriál: Mechanika Úvod Na úvod vás vítam pri čítaní druhej časti seriálu u. Začiatkom druhej série sa ešte raz vrátime k značeniu, kde si rýchlo ukážeme ako fungujú indexy, ktoré nám umožnia písať jednu
Seriál: Mechanika Úvod Na úvod vás vítam pri čítaní druhej časti seriálu u. Začiatkom druhej série sa ešte raz vrátime k značeniu, kde si rýchlo ukážeme ako fungujú indexy, ktoré nám umožnia písať jednu
Študijný program (Študijný odbor) Školiteľ Forma štúdia Téma Požiadavky na prijatie Výzbroj a technika ozbrojených síl (8.4.3 Výzbroj a technika ozbro
 (8.4.3 ) doc. Ing. Martin Marko, CSc. e mail: martin.marko@aos.sk tel.:0960 423878 Elektromagnetická kompatibilita mobilných platforiem komunikačných systémov. Zameranie: Analýza metód a prostriedkov vedúcich
(8.4.3 ) doc. Ing. Martin Marko, CSc. e mail: martin.marko@aos.sk tel.:0960 423878 Elektromagnetická kompatibilita mobilných platforiem komunikačných systémov. Zameranie: Analýza metód a prostriedkov vedúcich
Klasická metóda CPM
 Operačná analýza 2-02a Klasická metóda CPM Úvod Je daná úloha časového plánovania U s množinou elementárnych činností E a reálnou funkciou c: E R ktorá každej činnosti A E priradí jej dobu trvania c(a).
Operačná analýza 2-02a Klasická metóda CPM Úvod Je daná úloha časového plánovania U s množinou elementárnych činností E a reálnou funkciou c: E R ktorá každej činnosti A E priradí jej dobu trvania c(a).
Hranoly (11 hodín) September - 17 hodín Opakovanie - 8. ročník (6 hodín) Mesiac Matematika 9. ročník 5 hodín/týždeň 165 hodín/rok Tematický celok Poče
 Hranoly ( hodín) September - 7 hodín Opakovanie - 8. ročník (6 hodín) Mesiac Matematika 9. ročník 5 hodín/týždeň 65 hodín/rok Tematický celok Počet hodín 6 Téma Obsahový štandard Výkonový štandard Opakovanie
Hranoly ( hodín) September - 7 hodín Opakovanie - 8. ročník (6 hodín) Mesiac Matematika 9. ročník 5 hodín/týždeň 65 hodín/rok Tematický celok Počet hodín 6 Téma Obsahový štandard Výkonový štandard Opakovanie
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú in
 Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
px II. Reálna funkcia viac premenných (Prezentácia k prednáškam) Matematická analýza IV (ÚMV/MAN2d/10) RNDr. Lenka Halčinová, PhD.
 px (Prezentácia k prednáškam) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 21. marca 2019 Na úvod si zodpovedzme tieto otázky # 1 Prečo funkcia viac premenných? # 2 Čo sa očakáva, že v tejto chvíli mám v malíčku?
px (Prezentácia k prednáškam) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 21. marca 2019 Na úvod si zodpovedzme tieto otázky # 1 Prečo funkcia viac premenných? # 2 Čo sa očakáva, že v tejto chvíli mám v malíčku?
Technická Univerzita Košice Matematicko počítačové modelovanie Vysokoškolská učebnica Košice 2013
 Technická Univerzita Košice Matematicko počítačové modelovanie Vysokoškolská učebnica Košice 013 Technická Univerzita Košice Matematicko počítačové modelovanie Vysokoškolská učebnica Jozef Džurina Blanka
Technická Univerzita Košice Matematicko počítačové modelovanie Vysokoškolská učebnica Košice 013 Technická Univerzita Košice Matematicko počítačové modelovanie Vysokoškolská učebnica Jozef Džurina Blanka
(ıkolské kolo-PYT)
 Súťažné úlohy školského kola. Školský rok 2006/2007. Kategória P 3 1. Súčet dvoch čísel je 156. Prvý sčítanec je rozdiel čísel 86 a 34. Aký je druhý sčítanec? 2. Vypočítaj: 19 18 + 17 16 + 15 14 = 3. V
Súťažné úlohy školského kola. Školský rok 2006/2007. Kategória P 3 1. Súčet dvoch čísel je 156. Prvý sčítanec je rozdiel čísel 86 a 34. Aký je druhý sčítanec? 2. Vypočítaj: 19 18 + 17 16 + 15 14 = 3. V
text k predná²ke a úlohy k cvi eniam z vybraných kapitol z matematiky mi²o demetrian 1 1 Funkcionálne rady, rovnomerná konvergencia 1.1 ƒíselné rady -
 text k predná²ke a úohy k cvi eniam z vybraných kapito z matematiky mi²o demetrian Funkcionáne rady, rovnomerná konvergencia. ƒísené rady - opakovanie denícia konvergencie íseného radu: uvaºujeme ísený
text k predná²ke a úohy k cvi eniam z vybraných kapito z matematiky mi²o demetrian Funkcionáne rady, rovnomerná konvergencia. ƒísené rady - opakovanie denícia konvergencie íseného radu: uvaºujeme ísený
Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22
 Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22 Príklad 1 AR(2) proces z prednášky: x t =1.4x t 1 0.85x t 2 +u t V R-ku: korene charakteristického polynómu
Autoregresné (AR) procesy Beáta Stehlíková Časové rady, FMFI UK Autoregresné(AR) procesy p.1/22 Príklad 1 AR(2) proces z prednášky: x t =1.4x t 1 0.85x t 2 +u t V R-ku: korene charakteristického polynómu
Microsoft Word - Diskusia11.doc
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky MATEMATIKA - 011 sem vlepiť čiarový kód uchádzača Test obsahuje 30 úloh. Na jeho vypracovanie máte 90 minút. Každá úloha spolu
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky MATEMATIKA - 011 sem vlepiť čiarový kód uchádzača Test obsahuje 30 úloh. Na jeho vypracovanie máte 90 minút. Každá úloha spolu
Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovsk
 Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovská cesta 1, 034 01 Ružomberok, Slovakia e-mail: marian.trenkler@ku.sk
Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovská cesta 1, 034 01 Ružomberok, Slovakia e-mail: marian.trenkler@ku.sk
8
 8. Funkcie pre prácu s údajmi 8.1. Základné funkcie pre prácu s údajmi MATLAB umožňuje aj štatistické spracovanie údajov. Jednotlivé prvky sú zadávané ako matica (vektor). V prípade matice sa operácie
8. Funkcie pre prácu s údajmi 8.1. Základné funkcie pre prácu s údajmi MATLAB umožňuje aj štatistické spracovanie údajov. Jednotlivé prvky sú zadávané ako matica (vektor). V prípade matice sa operácie
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 Jednotkový koreň(unit roo
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Testy z CSS_2015_16
 Previerkové otázky na skúšku z ČSS 1. Vyjadrite slovne a matematicky princíp superpozície pre lineárnu diskrétnu sústavu. 2. Čo fyzikálne predstavuje riešenie homogénnej a nehomogénnej lineárnej diferenčne
Previerkové otázky na skúšku z ČSS 1. Vyjadrite slovne a matematicky princíp superpozície pre lineárnu diskrétnu sústavu. 2. Čo fyzikálne predstavuje riešenie homogénnej a nehomogénnej lineárnej diferenčne
Výsledky, návody a poznámky π π a. 5 1 ln 2. 6 π (π + 2). Návod: urobit substitúciu x = t a použit vetu 1.2.
 Výsledky, návody poznámky π 4. 3 π 3 3. 4. 5 ln. 6 π 7 8 4 (π + ). Návod: urobit substitúiu = t použit vetu.. 9 ln. 3 π Návod: vezmite do úvhy, že + 4 + = + + ( ) urobte substitúiu = t; dostnete dt t +,
Výsledky, návody poznámky π 4. 3 π 3 3. 4. 5 ln. 6 π 7 8 4 (π + ). Návod: urobit substitúiu = t použit vetu.. 9 ln. 3 π Návod: vezmite do úvhy, že + 4 + = + + ( ) urobte substitúiu = t; dostnete dt t +,
Snímka 1
 Fyzika - prednáška 12 Ciele 5. Fyzikálne polia 5.4 Stacionárne magnetické pole 5.5 Elektromagnetické pole Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Fyzika - prednáška 12 Ciele 5. Fyzikálne polia 5.4 Stacionárne magnetické pole 5.5 Elektromagnetické pole Zopakujte si Fyzikálne pole je definované ako... oblasť v určitom priestore, pričom v každom bode
Viacnásobne použitelné oblasti spolahlivosti pre viacrozmernú kalibráciu
 Viacnásobne použitel né oblasti spol ahlivosti pre viacrozmernú kalibráciu Martina Chvosteková Ústav merania Slovenská akadémia vied 22. január, Rekreačné zariadenie Rybník, 2018 Obsah 1 Predpoklady, model
Viacnásobne použitel né oblasti spol ahlivosti pre viacrozmernú kalibráciu Martina Chvosteková Ústav merania Slovenská akadémia vied 22. január, Rekreačné zariadenie Rybník, 2018 Obsah 1 Predpoklady, model
Seriál XXXII.IV Mechanika, FYKOS
 Seriál: Mechanika V tejto časti seriálu dokončíme príklad, ktorý sme minule začali - výpočet matematického kyvadla. K tomu ale budeme potrebovať vedieť, čo je to Taylorov rozvoj. Ďalej si ukážeme, ako
Seriál: Mechanika V tejto časti seriálu dokončíme príklad, ktorý sme minule začali - výpočet matematického kyvadla. K tomu ale budeme potrebovať vedieť, čo je to Taylorov rozvoj. Ďalej si ukážeme, ako
Úvodná prednáška z RaL
 Rozvrhovanie a logistika Základné informácie o predmete Logistika a jej ciele Štruktúra činností výrobnej logistiky Základné skupiny úloh výrobnej logistiky Metódy používané na riešenie úloh výrobnej logistiky
Rozvrhovanie a logistika Základné informácie o predmete Logistika a jej ciele Štruktúra činností výrobnej logistiky Základné skupiny úloh výrobnej logistiky Metódy používané na riešenie úloh výrobnej logistiky
Microsoft Word - mnohouholnik.doc
 Výpočet obsahu mnohouholníka Mnohouholník je daný súradnicami svojich vrcholov: A1[x1, y1], A2[x2, y2],..., An[xn, yn]. Aby sme sa vyhli komplikáciám, obmedzíme sa na prípad konvexného mnohouholníka. Súradnice
Výpočet obsahu mnohouholníka Mnohouholník je daný súradnicami svojich vrcholov: A1[x1, y1], A2[x2, y2],..., An[xn, yn]. Aby sme sa vyhli komplikáciám, obmedzíme sa na prípad konvexného mnohouholníka. Súradnice
Otázky k štátnej skúške z predmetu didaktika matematiky Prípravy študenta na štátnice - tvorba 14-tich rôznych príprav na vyučovaciu jednotku k temati
 Otázky k štátnej skúške z predmetu didaktika matematiky Prípravy študenta na štátnice - tvorba 14-tich rôznych príprav na vyučovaciu jednotku k tematickým okruhom uvedeným nižšie - vyučovacia jednotka
Otázky k štátnej skúške z predmetu didaktika matematiky Prípravy študenta na štátnice - tvorba 14-tich rôznych príprav na vyučovaciu jednotku k tematickým okruhom uvedeným nižšie - vyučovacia jednotka
MO_pred1
 Modelovanie a optimalizácia Ľudmila Jánošíková Katedra dopravných sietí Fakulta riadenia a informatiky Žilinská univerzita, Žilina Ludmila.Janosikova@fri.uniza.sk 041/5134 220 Modelovanie a optimalizácia
Modelovanie a optimalizácia Ľudmila Jánošíková Katedra dopravných sietí Fakulta riadenia a informatiky Žilinská univerzita, Žilina Ludmila.Janosikova@fri.uniza.sk 041/5134 220 Modelovanie a optimalizácia
Numerické riešenie všeobecnej (klasickej) DMPK rovnice.
 Numerické riešenie všeobecnej (klasickej) DMPK rovnice. J. Brndiar, R. Derian, P. Markos 11.6.27 1 Úvod Vodivost a transfér matica DMPK vs. zovšeobecnená DMPK rovnica 2 Numerické riešenie Ciel e Predpríprava
Numerické riešenie všeobecnej (klasickej) DMPK rovnice. J. Brndiar, R. Derian, P. Markos 11.6.27 1 Úvod Vodivost a transfér matica DMPK vs. zovšeobecnená DMPK rovnica 2 Numerické riešenie Ciel e Predpríprava
Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným
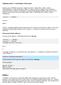 Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným dátovým typom je textový reťazec. Ako si môžeme predstaviť
Základy práce s textovými reťazcami Doteraz sme v MATLABe pracovali s datovými typmi: reálne číslo, vektor, matica. Veľmi dôležitým a často používaným dátovým typom je textový reťazec. Ako si môžeme predstaviť
Prezentace aplikace PowerPoint
 Ako vytvárať spätnú väzbu v interaktívnom matematickom učebnom prostredí Stanislav Lukáč, Jozef Sekerák Implementácia spätnej väzby Vysvetlenie riešenia problému, podnety pre konkrétne akcie vedúce k riešeniu
Ako vytvárať spätnú väzbu v interaktívnom matematickom učebnom prostredí Stanislav Lukáč, Jozef Sekerák Implementácia spätnej väzby Vysvetlenie riešenia problému, podnety pre konkrétne akcie vedúce k riešeniu
Katalóg cieľových požiadaviek k maturitnej skúške
 CIEĽOVÉ POŽIADAVKY NA VEDOMOSTI A ZRUČNOSTI MATURANTOV Z MATEMATIKY BRATISLAVA 2019 Schválilo Ministerstvo školstva, vedy, výskum a športu Slovenskej republiky dňa 12. júna 2019 pod číslom 2019/2049:2-A1020
CIEĽOVÉ POŽIADAVKY NA VEDOMOSTI A ZRUČNOSTI MATURANTOV Z MATEMATIKY BRATISLAVA 2019 Schválilo Ministerstvo školstva, vedy, výskum a športu Slovenskej republiky dňa 12. júna 2019 pod číslom 2019/2049:2-A1020
Operačná analýza 2
 Niektoré náhodné procesy majú v praxi veľký význam, pretože sa často vyskytujú, napr.: Poissonov proces proces vzniku a zániku Wienerov proces stacionárne procesy,... Poissonov proces je homogénny Markovov
Niektoré náhodné procesy majú v praxi veľký význam, pretože sa často vyskytujú, napr.: Poissonov proces proces vzniku a zániku Wienerov proces stacionárne procesy,... Poissonov proces je homogénny Markovov
1 Portál pre odborné publikovanie ISSN Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika
 1 Portál pre odborné publikovanie ISSN 1338-0087 Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika 28.04.2010 Článok spočíva v predstavení a opísaní algoritmu
1 Portál pre odborné publikovanie ISSN 1338-0087 Heuristický adaptívny PSD regulátor založený na miere kmitavosti Šlezárová Alexandra Elektrotechnika 28.04.2010 Článok spočíva v predstavení a opísaní algoritmu
Statika konštrukcií - prednášky
 PEDAGOGICKÁ DOKUMENTÁCIA PREDMETU Názov : Statika konštrukcií Identifikačné číslo : B-501205 Garantujúca katedra, ústav : Katedra stavebnej mechaniky, Ústav inžinierskeho staviteľstva Študijný odbor :
PEDAGOGICKÁ DOKUMENTÁCIA PREDMETU Názov : Statika konštrukcií Identifikačné číslo : B-501205 Garantujúca katedra, ústav : Katedra stavebnej mechaniky, Ústav inžinierskeho staviteľstva Študijný odbor :
Republika Srbsko MINISTERSTVO OSVETY, VEDY A TECHNOLOGICKÉHO ROZVOJA ÚSTAV PRE HODNOTENIE KVALITY VZDELÁVANIA A VÝCHOVY VOJVODINSKÝ PEDAGOGICKÝ ÚSTAV
 Republika Srbsko MINISTERSTVO OSVETY, VEDY A TECHNOLOGICKÉHO ROZVOJA ÚSTAV PRE HODNOTENIE KVALITY VZDELÁVANIA A VÝCHOVY VOJVODINSKÝ PEDAGOGICKÝ ÚSTAV ZÁVEREČNÁ SKÚŠKA NA KONCI ZÁKLADNÉHO VZDELÁVANIA A
Republika Srbsko MINISTERSTVO OSVETY, VEDY A TECHNOLOGICKÉHO ROZVOJA ÚSTAV PRE HODNOTENIE KVALITY VZDELÁVANIA A VÝCHOVY VOJVODINSKÝ PEDAGOGICKÝ ÚSTAV ZÁVEREČNÁ SKÚŠKA NA KONCI ZÁKLADNÉHO VZDELÁVANIA A
Microsoft Word - Argumentation_presentation.doc
 ARGUMENTÁCIA V. Kvasnička Ústav aplikovanej informatiky FIIT STU Seminár UI, dňa 21.11.2008 Priesvitka 1 Úvodné poznámky Argumentácia patrí medzi dôležité aspekty ľudskej inteligencie. Integrálnou súčasťou
ARGUMENTÁCIA V. Kvasnička Ústav aplikovanej informatiky FIIT STU Seminár UI, dňa 21.11.2008 Priesvitka 1 Úvodné poznámky Argumentácia patrí medzi dôležité aspekty ľudskej inteligencie. Integrálnou súčasťou
1)
 Prijímacia skúška z matematiky do prímy gymnázia s osemročným štúdiom Milá žiačka/milý žiak, sme veľmi radi, že ste sa rozhodli podať prihlášku na našu školu. Dúfame, že nasledujúce úlohy hravo vyriešite
Prijímacia skúška z matematiky do prímy gymnázia s osemročným štúdiom Milá žiačka/milý žiak, sme veľmi radi, že ste sa rozhodli podať prihlášku na našu školu. Dúfame, že nasledujúce úlohy hravo vyriešite
ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30
 ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30 ARMA modely - motivácia I. Odhadneme ACF a PACF pre dáta a nepodobajú sa
ARMA modely čast 3: zmiešané modely (ARMA) Beáta Stehlíková Časové rady, FMFI UK ARMA modely časť 3: zmiešané modely(arma) p.1/30 ARMA modely - motivácia I. Odhadneme ACF a PACF pre dáta a nepodobajú sa
Poznámky k cvičeniu č. 2
 Formálne jazyky a automaty (1) Zimný semester 2017/18 Zobrazenia, obrazy a inverzné obrazy Poznámky k cvičeniu č. 2 Peter Kostolányi 4. októbra 2017 Nech f : X Y je zobrazenie. Obraz prvku x X pri zobrazení
Formálne jazyky a automaty (1) Zimný semester 2017/18 Zobrazenia, obrazy a inverzné obrazy Poznámky k cvičeniu č. 2 Peter Kostolányi 4. októbra 2017 Nech f : X Y je zobrazenie. Obraz prvku x X pri zobrazení
gis7 prifuk
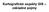 Kartografické aspekty GIS základné pojmy Kartografické aspekty GIS základné pojmy Referenčný elipsoid Geoid Povrch zeme Referenčný elipsoid Kartografické aspekty GIS základné pojmy Referenčný elipsoid
Kartografické aspekty GIS základné pojmy Kartografické aspekty GIS základné pojmy Referenčný elipsoid Geoid Povrch zeme Referenčný elipsoid Kartografické aspekty GIS základné pojmy Referenčný elipsoid
Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozos
![Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozos Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozos](/thumbs/101/150094868.jpg) Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval koval@fmph.uniba.sk 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozostávajúci z N nezávislých spinov. Každý zo spinov sa
Vybrané kapitoly zo štatistickej fyziky - domáce úlohy Michal Koval koval@fmph.uniba.sk 19. mája 2015 Domáca úloha č. 1 (pochádza z: [3]) Systém pozostávajúci z N nezávislých spinov. Každý zo spinov sa
Základy automatického riadenia - Prednáška 2
 Základy automatického riadenia Predná²ka 2 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita
Základy automatického riadenia Predná²ka 2 doc. Ing. Anna Jadlovská, PhD., doc. Ing. Ján Jadlovský, CSc. Katedra kybernetiky a umelej inteligencie Fakulta elektrotechniky a informatiky Technická univerzita
Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, prič
 Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, pričom to je veľmi dôležitá súčasť úlohy. Body sa udeľovali
Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, pričom to je veľmi dôležitá súčasť úlohy. Body sa udeľovali
Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 2017 Definície Žena - objekt ohodnotený celým číslom. Každé dve ženy sa dajú porovnat a
 Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 207 Definície Žena - objekt ohodnotený celým číslom. aždé dve ženy sa dajú porovnat a rozlíšit, t.j. žiadne dve nemajú rovanké hodnotenie.
Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 207 Definície Žena - objekt ohodnotený celým číslom. aždé dve ženy sa dajú porovnat a rozlíšit, t.j. žiadne dve nemajú rovanké hodnotenie.
ŠkVP_MAT
 Súkromné Gymnázium DSA, Komenského 40, 083 01 Sabinov MATEMATIKA Učebné osnovy 3. september 2018 Názov predmetu Časový rozsah výučby Názov ŠkVP Názov ŠVP Stupeň vzdelania Dĺžka štúdia Forma štúdia Vyučovací
Súkromné Gymnázium DSA, Komenského 40, 083 01 Sabinov MATEMATIKA Učebné osnovy 3. september 2018 Názov predmetu Časový rozsah výučby Názov ŠkVP Názov ŠVP Stupeň vzdelania Dĺžka štúdia Forma štúdia Vyučovací
Paralelné algoritmy, cast c. 2
 Paralelné algoritmy, čast č. 2 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 2 Paralelné algoritmy,
Paralelné algoritmy, čast č. 2 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 2 Paralelné algoritmy,
Obsah 1 Úvod Predhovor Sylaby a literatúra Základné označenia
 Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 4 1.3 Základné označenia................................. 4 2 Množiny a zobrazenia
Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 4 1.3 Základné označenia................................. 4 2 Množiny a zobrazenia
Obsah 1 Úvod Predhovor Sylaby a literatúra Základné označenia
 Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 4 1.3 Základné označenia................................. 4 2 Množiny a zobrazenia
Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 4 1.3 Základné označenia................................. 4 2 Množiny a zobrazenia
prijimacky 2014 MAT 4rocne ver A.doc
 Priezvisko a meno: " Sem nepíš! Kód: M-A-4r Kód: M-A-4r 1. súkromné gymnázium v Bratislave, Bajkalská 20, Bratislava Test z matematiky (verzia A 12. máj 2014) Pokyny pre žiakov 1. 2. Tento test obsahuje
Priezvisko a meno: " Sem nepíš! Kód: M-A-4r Kód: M-A-4r 1. súkromné gymnázium v Bratislave, Bajkalská 20, Bratislava Test z matematiky (verzia A 12. máj 2014) Pokyny pre žiakov 1. 2. Tento test obsahuje
Obsah
 Obsah str. 1. Základné pojmy pružnosti a pevnosti 1.1 Predmet a význam náuky o pružnosti a pevnosti 3 1.2 Z histórie oboru 3 1.3 Základné predpoklady o materiáli 4 1.4 Vonkajšie a vnútorné sily 5 1.5 Normálové
Obsah str. 1. Základné pojmy pružnosti a pevnosti 1.1 Predmet a význam náuky o pružnosti a pevnosti 3 1.2 Z histórie oboru 3 1.3 Základné predpoklady o materiáli 4 1.4 Vonkajšie a vnútorné sily 5 1.5 Normálové
PowerPoint Presentation
 Vymenujte základné body fyzikálneho programu ktoré určujú metodológiu fyziky pri štúdiu nejakého fyzikálneho systému Ako vyzerá pohybová rovnica pre predpovedanie budúcnosti častice v mechanike popíšte,
Vymenujte základné body fyzikálneho programu ktoré určujú metodológiu fyziky pri štúdiu nejakého fyzikálneho systému Ako vyzerá pohybová rovnica pre predpovedanie budúcnosti častice v mechanike popíšte,
