Slovenská komisia Matematickej olympiády FMFI UK, Mlynská dolina, Bratislava 51. ročník matematickej olympiády Riešenia úloh I. kola kategórie
|
|
|
- Otakar Kadlec
- pred 4 rokmi
- Prehliadani:
Prepis
1 Slovenská komisia Matematickej olympiády FMFI UK, Mlynská dolina, Bratislava 51. ročník matematickej olympiády Riešenia úloh I. kola kategórie P Tento pracovný materiál nie je určený priamo študentom účastníkom olympiády. Má pomôcť učiteľom na školách pri príprave konzultácií a pracovných seminárov pre riešiteľov súťaže, členom krajských výborov MO slúži ako podklad pre opravovanie úloh domáceho kola MO kategórie P. Študentom možno tieto komentáre poskytnúť až po termíne stanovenom pre odovzdanie riešení úloh domáceho kola MO kategórie P ako informáciu, ako bolo treba úlohy správne riešiť a pre ich odbornú prípravu na účasť v krajskom kole súťaže. P-I-1 Najskôr prevedieme úlohu do grafovej terminológie. Pojmom graf budeme nazývať usporiadanú dvojicu G = (V, E), kde E V V. Prvky množiny V sa nazývajú vrcholy grafu a prvky E (čo sú vlastne usporiadané dvojice vrcholov) hrany grafu. Vrcholy u, v V sú spojené hranou práve vtedy, keď (u, v) E. Bipartitný graf je taký graf, v ktorom môžeme vrcholy rozdeliť na dve disjunktné množiny R a S tak, aby každá hrana spájala vrchol z množiny R s vrcholom z množiny S. Štvorcovú maticu A núl a jednotiek rozmerov n n môžeme chápať aj ako reprezentáciu bipartitného grafu G s 2n vrcholmi, kde vrcholy r 1, r 2,... r n zodpovedajú riadkom a vrcholy s 1, s 2,..., s n zodpovedajú stĺpcom matice. Vrcholy r i a s j sú spojené hranou práve vtedy, keď prvok A[i, j] = 1. Hranu medzi r i a s j budeme značiť (r i, s j ). Hovoríme, že bipartitný graf má úplné párovanie, ak sa jeho vrcholy dajú usporiadať do dvojíc tak, že v každej dvojici je jeden vrchol z množiny S a jeden vrchol z množiny R a tieto dva vrcholy sú spojené hranou. Navyše, každý vrchol sa musí nachádzať práve v jednej takejto dvojici. Ukážeme, že ak bipartitný graf G má úplné párovanie, tak v našej matici A možno preusporiadať riadky a stĺpce takým spôsobom, aby na diagonále boli samé jednotky. Ak párovanie obsahuje dvojice (r i1, s j1 ), (r i2, s j2 ),..., (r in, s jn ), potom stačí riadky usporiadať v poradí i 1, i 2,..., i n a stĺpce v poradí j 1, j 2,..., j n. Označme takto preusporiadanú maticu A. Platí A [k, k] = A[i k, j k ]. Keďže medzi vrcholmi r ik a s jk v grafe G vedie hrana, platí, že A[i k, j k ] = 1, a preto matica A má na diagonále samé jednotky. Naopak, ak sa dá matica A preusporiadať tak, aby mala na diagonále samé jednotky, tak v grafe G existuje úplné párovanie. Nech v preusporiadanej matici A sú riadky v poradí i 1, i 2,..., i n a stĺpce v poradí j 1, j 2,..., j n. Vieme, že pre všetky k platí A [k, k] = 1, a preto aj A[i k, j k ] = 1. Preto v grafe G dvojice (r i1, s j1 ), (r i2, s j2 ),..., (r in, s jn ) tvoria úplné párovanie. Dokázali sme teda nasledujúce tvrdenie. Tvrdenie. Matica A sa dá transformovať na tvar s jednotkami na diagonále práve vtedy, keď existuje úplné párovanie v grafe G. Ak teda chceme zistiť, ako maticu A pretransformovať na tvar s jednotkami na diagonále, vypočítame najprv úplné párovanie v grafe G. Ak také párovanie existuje, preusporiadame riadky a stĺpce podľa postupu uvedeného vyššie. Ak také párovanie neexistuje, maticu nemožno transformovať. Jediným problémom zostáva ukázať, ako také úplné párovanie nájsť. 1
2 Pripomeňme, že v úplnom párovaní sú v každej dvojici vrcholy spojené hranou. Preto môžeme úplné párovanie chápať aj ako množinu hrán M takú, že každý vrchol grafu je koncovým vrcholom práve jednej hrany z M. Podobne môžeme zadefinovať párovanie ako množinu hrán M takú, že každý vrchol grafu je koncovým vrcholom najviac jednej hrany z M. To znamená, že v párovaní, ktoré nie je úplné, nie všetky vrcholy musia byť zaradené v niektorej dvojici. Ukážeme teraz algoritmus, ako nájsť v bipartitnom grafe maximálne párovanie, t.j. párovanie s najväčším počtom hrán. Maximálne párovanie budeme hľadať postupne. Začneme s prázdnym párovaním M = a v každom kroku zvýšime počet párovacích hrán o jedna. Ak sa nám v niektorom kroku nepodarí zvýšiť počet hrán v párovaní, vyhlásime aktuálne párovanie za maximálne a skončíme. Zvyšovať počet hrán v párovaní budeme pomocou takzvaných zlepšujúcich ciest. Uvažujme ľubovoľné pevne zvolené párovanie M. Alternujúca cesta pre párovanie M je postupnosť vrcholov r i1, s j1, r i2, s j2,..., r ik, s ik, ktorá začína nespárovaným riadkovým vrcholom, končí stĺpcovým vrcholom, každá dvojica po sebe nasledujúcich vrcholov je spojená hranou a striedajú sa párovacie a nepárovacie hrany (prvá hrana (r i1, s j1 ) je nepárovacia). Zlepšujúca cesta je alternujúca cesta, ktorá končí nespárovaným vrcholom. Všimnite si, že zlepšujúca cesta P = r i1, s j1, r i2, s j2,..., r ik, s ik pozostáva z k 1 párovacích a k nepárovacích hrán. Majme teda párovanie M a zlepšujúcu cestu P. Ak všetky párovacie hrany v P zmeníme na nepárovacie a naopak, dostaneme nové párovanie M, ktoré má o jednu hranu viac (uvedomte si, že M naozaj spĺňa podmienky párovania). M : s j1 s j2 s j3 s j4 M : s j1 s j2 s j3 s j4 r i1 r i2 r i3 r i4 r i1 r i2 r i3 r i4 (plné čiary sú párovacie, čiarkované čiary sú nepárovacie) Dokážme teraz, že našim postupom vždy dostaneme maximálne párovanie, t.j. že sa nám nestane, že neexistuje zlepšujúca cesta pre párovanie, ktoré nie je maximálne. Tvrdenie. Ak párovanie M nie je maximálne, existuje preňho zlepšujúca cesta v G. Dôkaz tvrdenia. Nech M je párovanie, ktoré nie je maximálne. Keďže M nie je maximálne, musí existovať párovanie M, ktoré obsahuje viac hrán ako M. Hrany patriace do M, avšak nie do M nazvime modré a hrany patriace do M avšak nie do M nazvime červené. Keďže M > M, červených hrán musí byť viac ako modrých. Uvažujme graf G tvorený všetkými modrými a červenými hranami. Každý vrchol v G susedí s najviac jednou modrou a jednou červenou hranou. Teda každý súvislý komponent grafu G musí byť buď kružnica alebo cesta, pričom na každej kružnici (ceste) sa striedajú červené a modré hrany. To znamená, že každá kružnica obsahuje rovnako veľa modrých a červených hrán; počty červených a modrých hrán na každej ceste sa líšia najviac o 1. Keďže červených hrán je viacej ako modrých, musí existovať komponent P, ktorý obsahuje viac červených hrán ako modrých. Takýto komponent musí byť cesta, ktorá začína aj končí červenou hranou. Teda cesta P obsahuje nepárny počet hrán. Z toho vyplýva, že jeden z jej koncov musí byť riadkový vrchol (nazvime ho r i ) a druhý stĺpcový vrchol (nazvime ho s j ). Je ľahké presvedčiť sa, že keďže r i resp. s j je nespárovaný riadkový resp. stĺpcový vrchol a každá druhá hrana patrí do párovania M, P je zlepšujúca cesta pre M. Implementácia. Graf G reprezentujeme samotnou maticou, t.j. dvojrozmerným poľom A. Pre každý vrchol r i (s j ) si v poli par r (par s) pamätáme, či je spárovaný s nejakým vrcholom a ak áno, číslo tohoto vrchola. Začneme so všetkými vrcholmi nespárovanými. Funkcia Zlepsi 2
3 hľadá zlepšujúcu cestu a ak ju nájde, použije ju na zlepšenie aktuálneho párovania. Hľadanie je implementované prehľadávaním do šírky zo všetkých vrcholov r i, ktoré ešte nie sú spárované. Ak nájde alternujúcu cestu do nespárovaného vrchola s j, prehľadávanie skončí. V tomto okamihu je potrebné prejsť po nájdenej ceste z s j späť do r i, zmeniť párovacie hrany na nepárovacie a naopak, čo znamená aktualizovanie záznamov v par r (par s) pre všetky vrcholy na nájdenej ceste. Funkcia Zlepsi je volaná v cykle, kým je možné zvyšovať počet hrán v párovaní. Ak vylepšenie párovania úspešne zbehne n krát, máme úplné párovanie, ktoré použijeme na preusporiadanie matice do požadovaného tvaru. V opačnom prípade podáme správu o tom, že matica sa usporiadať nedá. Časová zložitosť: každé volanie Zlepsi zbehne v čase O(n 2 ), spolu potrebujeme nanajvýš n volaní, čo dáva celkový čas O(n 3 ). Na uloženie matice A potrebujeme pamäť O(n 2 ). program P I 1; const MAXN = 100; var f, g : text; A : array[1..maxn, 1..MAXN] of integer; par r, par s : array[1..maxn] of integer; N : integer; function Zlepsi : boolean; {ak sa dá, zvýši počet párov o 1} var buf, back : array[0..maxn] of integer; zbuf, kbuf, vi, vj, i, j, tmp : integer; nasiel : boolean; Begin zbuf := 0; kbuf := 0; for i := 1 to N do if par r[i] <= 0 then buf[kbuf] := i; Inc(kbuf); for j := 1 to N do back[j] := 0; nasiel := false; while (zbuf < kbuf) and not nasiel do vi := buf[zbuf]; Inc(zbuf); for j := 1 to N do if nasiel then break; if (A[vi, j] = 0) or (j = par r[vi]) or (back[j] > 0) then continue; if par s[j] <= 0 then {našli sme zlepšujúcu cestu} nasiel := true; vj := j; while true do par s[vj] := vi; tmp := par r[vi]; par r[vi] := vj; vj := tmp; if vj <= 0 then break; 3
4 vi := back[vj]; end else {pokračujeme v hľadaní} back[j] := vi; buf[kbuf] := par s[j]; Inc(kbuf); Zlepsi := nasiel; End; procedure Uprac stlpce; var i, j, tmp, ii : integer; Begin for i := 1 to n do while par r[i] <> i do ii := par r[i]; for j := 1 to n do tmp := A[i, j]; A[i, j] := A[ii, j]; A[ii, j] := tmp; par r[i] := par r[ii]; par r[ii] := ii; End; var i, j : integer; ok : boolean; Begin Assign(f, matica.in ); Reset(f); Assign(g, matica.out ); ReWrite(g); ReadLn(f, N); for i := 1 to N do for j := 1 to N do Read(f, A[i, j]); {párovanie} for i := 1 to N do ok := Zlepsi; if not ok then break; if not ok then WriteLn(g, Maticu nemozno transformovat. ) else Uprac stlpce; for i := 1 to n do for j := 1 to n do Write(g, A[i, j]); if j < n then Write(g, ) else WriteLn(g); 4
5 Close(g); Close(f); End. P-I-2 Úlohu najprv preformulujeme do reči teórie grafov. Uzly budeme nazývať vrcholmi, rúry hranami a celú sústavu potrubí budeme volať graf. Postupnosť (nie nutne rôznych) vrcholov a hrán v 0, e 1, v 1, e 2,..., v k 1 e k, v k nazveme sled, ak každá hrana e i spája vrcholy v i 1 a v i. Ak navyše v 0 = v k, takýto sled nazveme uzavretý. V reči grafov, úlohou bolo v danom súvislom grafe G nájsť uzavretý sled, ktorý prejde každú hranu grafu práve dvakrát. Ukážeme algoritmus, ktorý pre ľubovoľný súvislý graf nájde požadovaný sled (tento algoritmus je teda vlastne dôkazom, že trasa pre robota vždy existuje). Naše riešenie je založené na prehľadávaní do hĺbky. O každom vrchole si budeme pamätať, či sme ho už v priebehu algoritmu niekedy navštívili. Pre každý navštívený vrchol v, nech rodic[v] označuje vrchol, z ktorého robot do v prvýkrát prišiel. Vrchol rodic[v] je rodičom vrchola v; podobne v je potomkom vrchola rodic[v]. Pre vrchol 1 nie je rodic[1] definovaný. Prehľadávanie do hĺbky začína z vrchola 1 a funguje takto: 1. Označ aktuálny vrchol v ako navštívený. 2. Postupne kontroluj všetky hrany idúce z v a vždy keď nájdeš takú hranu, ktorá vedie do ešte nenavštíveného vrchola u, prejdi robotom do vrchola u a pokračuj rekurzívne v prehľadávaní z u (v sa stane rodičom u). 3. Keď sú všetky hrany z v skontrolované a v 1, vráť sa do vrchola rodic[v] (a pokračuj v kontrolovaní jeho hrán). Ak v = 1, skonči. Uvažujme množinu hrán, po ktorých robot prvýkrát prišiel do nejakého vrchola; sú to práve hrany (rodic[v], v), pre tie v, pre ktoré je rodic[v] definovaný. Nazvime tieto hrany stromové (nazývajú sa tak, lebo tieto hrany tvoria súvislý graf neobsahujúci kružnicu, nazývaný tiež strom). Každú stromovú hranu (u, v), kde u je rodičom v, prejde robot pri prehľadávaní práve dvakrát najprv z vrchola u prvýkrát navštívi vrchol v a druhýkrát pri návrate z vrchola v do vrchola u. Pri prehľadávaní robot nikdy neprejde po nestromovej hrane (keď prechádza po hrane (u, v), buď navštevuje vrchol v prvýkrát, čím sa hrana (u, v) stane stromovou, alebo sa vracia z vrchola u do vrchola v a to vždy po stromovej hrane). Keďže náš graf G je súvislý, robot pri prehľadávaní navštívi všetky vrcholy. Keby totiž existoval nenavštívený vrchol, musel by existovať taký navštívený vrchol u a nenavštívený vrchol v, že u a v sú spojené hranou. To však nie je možné, lebo algoritmus prehľadávania sa z vrchola u do rodic[u] nevráti, kým nie sú všetci susedia u navštívení. Prehľadávanie do hĺbky navštívi každý vrchol a prejde každú stromovú hranu práve dvakrát; ostáva nám rozhodnúť kedy a ako bude robot prechádzať nestromové hrany. Počas prehľadávania je jednoduché detekovať nestromové hrany. Ak sa robot práve nachádza vo vrchole u a kontroluje hranu (u, v), táto hrana je nestromová, ak vrchol v už bol navštívený a u nie je rodičom v ani v nie je rodičom u. Ak robot nachádzajúci sa vo vrchole u narazí na nestromovú hranu (u, v), môže ju vyčistiť prejdením do v a späť za predpokladu, že ňou už predtým neprešiel. Preto si pre každú hranu budeme pamätať, či už bola vyčistená alebo nie. Implementácia. Prehľadávanie do hĺbky je implementované rekurzívnou procedúrou Prehladaj. Keďže rekurzia si pre aktuálny vrchol automaticky pamätá jeho rodiča, nie je nutné 5
6 explicitne udržiavať záznamy rodic[v]. Vo vzorovom programe graf reprezentujeme maticou n n, z čoho vyplýva časová aj pamäťová zložitosť programu O(n 2 ). Efektívnejšou reprezentáciou hrán pomocou spájaného zoznamu je možné dosiahnuť časovú aj pamäťovú zložitosť O(m + n), kde m je počet hrán grafu, avšak za cenu mierne zložitejšieho programu. Poznámka. Úlohu bolo možné riešiť aj pomocou algoritmov na hľadanie eulerovského ťahu (t.j. sledu, ktorý obsahuje každú hranu práve raz). Stačí náš graf pozmeniť tak, že každú hranu skopírujeme dvakrát a v tomto grafe nájsť eulerovský ťah (ten vždy existuje, lebo každý vrchol v novom grafe bude mať párny stupeň). Tento typ riešenia nebudeme podrobnejšie popisovať. program P I 2; const MAXN = 100; {max. počet vrcholov } HR HRANA = 1; {typy hrán - neprejdená, } HR STROMOVA = 2; { stromová a } HR PREJDENA = 3; { nestromová prejdená } var f, g : text; n, m : integer; hr : array[1..maxn, 1..MAXN] of integer; bol : array[1..maxn] of boolean; procedure Prehladaj(v : integer); var i : integer; Begin WriteLn(g, v); bol[v] := true; for i := 1 to n do if hr[v][i] <> 1 then continue; if bol[i] then {nestromová neprejdená hrana} WriteLn(g, i); hr[v, i] := HR PREJDENA; hr[i, v] := HR PREJDENA; End; end else hr[v, i] := HR STROMOVA; hr[i, v] := HR STROMOVA; Prehladaj(i); WriteLn(g, v); {stromová neprejdená hrana} {Prehľadaj} var i, j, aa, bb : integer; Begin Assign(f, rury.in ); Reset(f); Assign(g, rury.out ); ReWrite(g); ReadLn(f, n, m); for i := 1 to n do for j := 1 to n do hr[i, j] := 0; for i := 1 to m do ReadLn(f, aa, bb); 6
7 hr[aa, bb] := HR HRANA; hr[bb, aa] := HR HRANA; for i := 1 to n do bol[i] := false; Prehladaj(1); Close(g); Close(f); End. P-I-3 Dokážme najprv, že spravodlivá priamka vždy existuje. Vezmime ľubovoľnú orientovanú priamku idúcu cez bod [0, 0] a nech x je rozdiel počtu bielych bodov naľavo a čiernych bodov napravo. Ak je x nula, priamka je spravodlivá. Ak nie, budeme priamku otáčať okolo bodu [0, 0]. Vždy keď priamka prejde cez biely alebo čierny bod, hodnota x sa zníži alebo zvýši o jedna. Keď priamku otočíme presne o 180, naša sledovaná hodnota prešla z počiatočného x na x (lebo všetky body, ktoré boli pôvodne naľavo, sú teraz napravo a naopak). To znamená, že hodnota musela byť aspoň pri jednej polohe priamky nulová. V tejto polohe je priamka spravodlivá. Budeme vravieť, že bod A je naľavo od bodu B, ak je naľavo od orientovanej priamky idúcej z [0, 0] do A. Základom algoritmu je nasledujúce pozorovanie. Vezmime spravodlivú priamku p. Nech A je prvý bod, na ktorý by sme narazili, ak by sme priamku p otáčali v smere hodinových ručičiek. Bod A a všetky body, ktoré sú od neho napravo, sú v jednej polrovine určenej priamkou p. Body, ktoré sú od A naľavo, sú v druhej polrovine. Vidíme teda, že nezáleží na konkrétnej polohe priamky p, rozdelenie bodov je určené polohou hraničného bodu A. Stačí teda zobrať každý bod ako kandidáta na bod A, zrátať počet bielych a čiernych bodov naľavo a napravo a skontrolovať, či počty spĺňajú podmienky spravodlivej priamky. Ak nájdeme úspešného kandidáta, spravodlivú priamku zostrojíme tak, že priamku idúcu cez bod otočíme kúsok proti smeru hodinových ručičiek tak, aby sme neprešli cez žiaden iný bod. V praxi sa to dá spraviť tak, že nájdeme prvý bod X, cez ktorý by sme pri takom otáčaní prešli a priamku vedieme stredom medzi kandidátom A a bodom X. Takto dostaneme algoritmus s časovou zložitosťou O(n 2 ) (pre každého kandidáta zisťujeme polohu každého bodu vzhľadom na tohto kandidáta). Algoritmus však možno zefektívniť tým, že si body najprv utriedime v smere hodinových ručičiek okolo bodu [0, 0]. Kandidátov na hraničný bod A budeme skúšať v tomto utriedenom poradí. Keď sa presunieme z kandidáta i 1 na kandidáta i, nemusíme už pre každý bod zisťovať, či je od bodu i naľavo alebo napravo, lebo veľa bodov zostane v tej istej polrovine. Budeme si teda v každom kroku udržovať počet bielych a čiernych bodov v pravej polrovine a index j ukazujúci na posledný bod v pravej polrovine v smere hodinových ručičiek. Keď se presunieme na kandidáta i, stačí bod i 1 presunúť do ľavej polroviny (t.j. odpočítať z počtu bodov príslušnej farby, ktoré sú v pravej polrovine) a potom posúvať index j v smere hodinových ručičiek, kým nenájdeme prvý bod, ktorý je naľavo od bodu i. Všetky body, cez ktoré sme s indexom j prešli, sa presunú z ľavej polroviny do pravej a treba ich teda pripočítať k počtu bodov príslušnej farby. Keď pri posúvaní bodu j prídeme na koniec poľa, pokračujeme zase cyklicky od začiatku. Netreba zabudnúť ošetriť okrajové prípady, keď napríklad všetky body sú od bodu j naľavo alebo napravo. Utriediť body v smere hodinových ručičiek môžeme v čase O(n log n) niektorým so štandard- 7
8 ných triediacich algoritmov. Iba namiesto bežného porovnania si potrebujeme napísať funkciu, ktorá pre dva body určí, ktorý z nich má väčší uhol. V priloženom programe sme pre jednoduchosť použili triedenie pracujúce v čase O(n 2 ), to však možno ľahko nahradiť iným. Pre prvý bod musíme prejsť všetky body a zistiť, ktoré sú vľavo (v čase O(n)). Pre každý ďalší bod už len budeme posúvať indexy i a j a sledovať iba body, cez ktoré prechádzame. Cez každý bod prejdeme každým indexom najviac raz a teda celkový čas posúvania pre všetky kandidátske body spolu bude O(n). Celková časová zložitosť algoritmu je teda O(n log n) a pamäťová zložitosť je O(n). program p I 3; const napriamke = 0; napravo = 1; nalavo = 2; {smery} biela = 0; cierna = 1; {farby} type bod = record x, y : longint; farba : integer; var n : integer; {počet bielych/čiernych bodov} m : integer; {celkový počet bodov} a : array[ ] of bod; {pole bodov} {pocet bielych a čiernych bodov napravo do priamky} pocet : array[biela..cierna] of integer; start : bod; {štartovací bod triedenia} function poloha(a, b : bod) : integer; {Zisti, kde je bod b vzhľadom na priamku cez body (0,0),a} var vektsucin : longint; vektsucin := a.x b.y b.x a.y; if vektsucin > 0 then poloha := nalavo else if vektsucin < 0 then poloha := napravo else poloha := napriamke {poloha} function mensi(var a, b : bod) : boolean; {Vráti, či bod a je menší ako bod b v našom usporiadaní} var pol1, pol2, pol3 : integer; pol1 := poloha(start, a); pol2 := poloha(start, b); pol3 := poloha(a, b); mensi := (pol1 < pol2) or ((pol1 = pol2) and (pol3 = napravo)); {mensi} procedure tried; {Utriedi body pomocou porovnania mensi } var i, j, min : integer; pom : bod; for i := 1 to m 1 do min := i; {nájdi minimum v a[i..m]} for j := i + 1 to m do if mensi(a[j], a[min]) then min := j; 8
9 {ulož minimum do a[i]} pom := a[i]; a[i] := a[min]; a[min] := pom; {tried} procedure nacitaj; {Načíta dáta zo súboru} var t : text; i : integer; assign(t, priamka.in ); {otvor súbor} reset(t); read(t, n); {počet bielych/čiernych bodov} m := 2 n; {celkový počet bodov} for i := 1 to m do {čítaj body} read(t, a[i].x, a[i].y); if i <= n then a[i].farba := biela else a[i].farba := cierna; close(t); {zavri súbor} {nacitaj} function prva priamka : integer; {Nájdi priamku idúcu tesne pred bod a[1], vráť posledný bod napravo, inicializuj pole pocet} var i : integer; pocet[biela] := 0; {vynuluj počty} pocet[cierna] := 0; i := 1; {kým sme napravo, zvyšuj pole pocet} while (i <= m) and (poloha(a[1], a[i]) in [napravo, napriamke]) do pocet[a[i].farba] := pocet[a[i].farba] + 1; i := i + 1; prva priamka := i 1; {prva priamka} function dalsia priamka(i, j : integer) : integer; {Posunie priamku spred bodu a[i-1] pred bod a[i]} var koniec : boolean; stare j : integer; {a[i-1] sa posunie doľava - odčítaj ho} pocet[a[i 1].farba] := pocet[a[i 1].farba] 1; koniec := false; repeat stare j := j; j := j + 1; {pričítaj body, ktoré sa posunú doprava} 9
10 if j > m then j := 1; if (poloha(a[i], a[j]) in [napravo, napriamke]) then pocet[a[j].farba] := pocet[a[j].farba] + 1; end else koniec := true; until koniec or (j = i); dalsia priamka := stare j; {dalsia priamka} procedure vypis(i, j : integer); {Vypíše výsledok do súboru} var t : text; b1, b2 : bod; {b1 je a[i] premietnuté podľa (0,0)} b1.x := a[j].x; b1.y := a[j].y; {b2 je posledný bod pred a[i]} if i > 1 then b2 := a[i 1] else b2 := a[m]; {nájdi ten z b1, b2, ktorý je viac vpravo} if (poloha(a[i], b2) = nalavo) and (poloha(b1, b2) = napravo) then b1 := b2; assign(t, priamka.out ); {otvor súbor} rewrite(t); {výsledný bod je stred úsečky medzi a[i] a b1} writeln(t, (a[i].x + b1.x)/2.0 : 0 : 1,, (a[i].y + b1.y)/2.0 : 0 : 1); close(t); {zatvor súbor} {vypis} var i, j : integer; {hlavný program} nacitaj; {načítaj vstup} start := a[1]; {od tohoto bodu začneme triediť} tried; {utrieď proti smeru hodinových ručičiek} i := 1; j := prva priamka; {nájdi prvú priamku} {kým nenájdeš čo potrebuješ, skúšaj ďalšiu priamku} while pocet[biela] <> n pocet[cierna] do i := i + 1; j := dalsia priamka(i, j); vypis(i, j); {vypíš do výstupného súboru} end. P-I-4 Časť a. Najskôr popíšme formát vstupného súboru, aký sme si zvolili (váš program samozrejme môže používať iný formát). Vstupný súbor obsahuje na prvom riadku počet vodičov a počet komparátorov, na druhom riadku vstupy siete od vrchného vodiča po spodný a zvyšné riadky 10
11 obsahujú popis siete. Každý komparátor je daný dvoma číslami zapísanými na jednom riadku. Tieto čísla určujú vrchný a spodný vodič spojený komparátorom. Vodiče sú číslované zhora nadol začínajúc od jedna. Komparátory sú zadané v poradí zľava doprava. Jednotlivé vrstvy siete sú oddelené riadkom obsahujúcim dve nuly. Program uvedený v tomto vzorovom riešení pre jednoduchosť zobrazuje výpočet siete semigraficky. Najprv načíta vstup, pričom všetky komparátory a oddeľovače vrstiev uloží do jedného pola. Potom vykresľuje samotnú sieť zľava doprava. Zakaždým, keď vykreslí komparátor, odsimuluje jeho činnosť na aktuálnom stave vodičov. To znamená, že porovná príslušné dve hodnoty v poli, a ak sú v opačnom poradí, tak ich vymení. Po skončení každej vrstvy (t.j. vždy, keď narazí na oddeľovač v zozname komparátorov) program vypíše aktuálny stav hodnôt na vodičoch. Jediný problém, ktorý zostáva vyriešiť, je ako umiestniť jednotlivé komparátory v jednej vrstve do stĺpcov, tak aby sa žiadne dva komparátory v jednom stĺpci neprekrývali. Náš program si preto pamätá, ktoré z vodičov sú v aktuálnom stĺpci už obsadené komparátorom. Ak sa ďalší komparátor prekrýva s niektorým komparátorom v aktuálnom stĺpci, začneme nový stĺpec a komparátor umiestnime do nového stĺpca. Celková časová zložitosť nášho programu je úmerná veľkosti nakresleného obrázku, t.j. O(nk), kde n je počet vodičov a k je počet stĺpcov, v ktorých sú komparátory vykreslené. Na záver uveďme príklad vstupu a výstupu z nášho programu (ide o sieť uvedenú v študijnom texte). Vstup: 1. časť: časť: Výstup: 4--* * *--1--*--3--* *--2--*--2--* * * Časť b. Sieť zostrojíme rekurzívne. Označme S n sieť, ktorá úlohu rieši pre n vstupov. Sieť S 1 neobsahuje žiaden komparátor, lebo máme iba jeden vstup a ten je utriedený. Predpokladajme, že n > 1. Prvá vrstva siete obsahuje iba jeden komparátor medzi vodičmi n a n/2. Potom rozdelíme n vodičov na dve polovice hornú a dolnú a na každú polovicu použijeme sieť S n/2. Tieto dve podsiete budú pracovať paralelne. Konštrukcia siete S n je zobrazená na nasledujúcom obrázku vľavo, vpravo je príklad výslednej siete pre n = 8. n 2 n 2.. S n/2 S n/2 Uvedomme si najprv, prečo takto zostavená sieť rieši zadanú úlohu. Označme vstupné hodnoty siete x 1, x 2,..., x n. Môžu nastať dva prípady podľa toho, či je x n menšie alebo väčšie ako x n/2. Predpokladajme najprv, že x n x n/2. Vtedy komparátor v prvej vrstve nevymení vstupné hodnoty. Nakoľko x n x n/2, prvok x n patrí v usporiadanom poradí na niektorý zo spodnej polovice vodičov. Po prvom kroku výpočtu teda platí, že horná polovica je celá utriedená a obsahuje n/2 najmenších prvkov zo vstupu. Dolná polovica je utriedená s prípadnou výnimkou posledného 11
12 prvku a obsahuje n/2 najväčších prvkov. Preto vstupy oboch podsietí S n/2 spĺňajú podmienku zo zadania, že všetky hodnoty okrem poslednej majú byť na vstupe utriedené (to nevylučuje prípad, že aj posledná hodnota bude utriedená). Teda na výstupe budú obe polovice v utriedenom poradí. Keďže už po prvom kroku každá polovica obsahovala tie správne prvky, aj celá postupnosť je v utriedenom poradí. Druhý prípad nastane, ak x n < x n/2. Vtedy komparátor vymení hodnoty. Vieme, že x n patrí niekde do hornej polovice prvkov a dostane sa na najspodnejší vodič hornej polovice. Naopak, posledný prvok z hornej polovice, t.j. x n/2, patrí v skutočnosti do dolnej polovice (pri triedení je vytlačený prvkom x n ). Prvok x n/2 sa ale prvým komparátorom dostane na najspodnejší vodič, t.j. do dolnej polovice. Podobne ako predtým, aj teraz máme po prvom kroku v každej polovici tie prvky, ktoré tam v utriedenom poradí patria. Taktiež obe polovice sú utriedené s prípadnou výnimkou najspodnejšieho prvku. Teda po aplikovaní podsietí S n/2 dostaneme dve utriedené polovice, ktoré spolu tvoria utriedenú postupnosť. Hĺbka rekurzie je v našej konštrukcii log 2 n, lebo každá úroveň rekurzie zmenší počet vodičov na polovicu. V každej úrovni rekurzie pridáme jednu vrstvu, celkový počet vrstiev je teda tiež log 2 n. Prvá vrstva obsahuje 1 komparátor, v každej ďalšej vrstve sa počet komparátorov zdvojnásobí. Nech počet vstupov je n = 2 k. Potom počet použitých komparátorov je k 1 = 2 k 1 = n 1 (súčet geometrickej postupnosti). Naša sieť teda má O(log n) vrstiev a používa O(n) komparátorov. program P I 4a; {program semigraficky zobrazí priebeh výpočtu komparátorovej siete} uses crt; const MAXM = 100; {maximálny počet komparátorov} MAXN = 100; {maximálny počet vodičov} var n : integer; {počet vodičov} poloziek : integer; {počet položiek v poli komparatory} komparatory : array[1..2 MAXM, 1..2] of integer; {zoznam komparátorov a oddeľovačov úrovní} stav : array[1..maxn] of integer; {aktuálny stav vodičov po niekoľkých krokoch} plne : array[1..maxn] of boolean; {či ide cez vodič čiara v aktuálnom stľpci} procedure nacitaj; var inp : text; {vstupný súbor} i, komparatorov, bolo komparatorov : integer; assign(inp, siete.in ); {otvor vstupný súbor} reset(inp); read(inp, n, komparatorov); {čítaj počet vodičov a komparátorov} for i := 1 to n do {načítaj vstupy siete - (stav vodičov)} read(inp, stav[i]); {načítavaj komparátory a oddeľovače, až kým nedosiahneš daný počet komparátorov} bolo komparatorov := 1; poloziek := 0; while bolo komparatorov <= komparatorov do 12
13 poloziek := poloziek + 1; read(inp, komparatory[poloziek, 1], komparatory[poloziek, 2]); {ak položka bola komparátor, zvýs počet komparátorov} if komparatory[poloziek, 1] <> 0 then bolo komparatorov := bolo komparatorov + 1; {za posledným načítaným komparátorom pridaj oddeľovač} poloziek := poloziek + 1; komparatory[poloziek, 1] := 0; komparatory[poloziek, 2] := 0; close(inp); {zatvor vstupný súbor} { nacitaj } procedure prazdne stlpce(stlpec, kolko : integer); var i, j : integer; {vypis <kolko> prázdnych stľpcov} for i := 1 to n do gotoxy(stlpec, i 2 1); for j := 1 to kolko do write( - ); { prazdne stlpce } procedure vypis stav(stlpec, sirka : integer); var i : integer; for i := 1 to n do {vypíš aktuálny stav vodičov} gotoxy(stlpec, i 2 1); write(stav[i] : sirka); { vypis stav } {každé číslo má šírku <sirka>} function najdi sirku : integer; var i, max, sirka, cislo : integer; {najde šírku (počet miest) najširšieho čísla na vstupe} max := 1; for i := 1 to n do sirka := 1; cislo := stav[i]; {nájdi šírku čísla stav[i]} while cislo >= 10 do sirka := sirka + 1; {del 10, kým neklesneš pod 10} cislo := cislo div 10; if sirka > max then max := sirka; {porovnaj s maximom} najdi sirku := max; { najdi sirku } function je volno(odkial, pokial : integer) : boolean; var i : integer; 13
14 ok : boolean; {zisti, či môžeme zakresliť komparátor do stĺpca} ok := true; for i := odkial to pokial do if plne[i] then ok := false; je volno := ok; { je volno } {ak sa kríži s iným, nemôžeme} procedure spracuj komparator(odkial, pokial, stlpec : integer); var i, pom : integer; {vykresli jeden komparátor, zapíš do pola plne, meň stav} gotoxy(stlpec, 2 odkial 1); {vykresli horný koniec} write( * ); gotoxy(stlpec, 2 pokial 1); {vykresli dolný koniec} write( * ); for i := 2 odkial to 2 pokial 2 do {spojnica medzi} gotoxy(stlpec, i); write( ); for i := odkial to pokial do {zapíš komparátor do pola plne} plne[i] := true; {vykonaj porovnanie a výmenu danú komparátorom} if stav[odkial] > stav[pokial] then pom := stav[odkial]; stav[odkial] := stav[pokial]; stav[pokial] := pom; { vykresli komparator } procedure vykresli; var i, j, stlpec, sirka : integer; novy stlpec : boolean; {vykresli celý priebeh výpočtu} clrscr; {zmaž obrazovku} sirka := najdi sirku; {nájdi šírku čísla na vodiči} vypis stav(1, sirka); {vypíš vstupy do stĺpca 1} stlpec := sirka; {posledný použitý stĺpec je <sirka>} novy stlpec := true; {v tomto stĺpci nebol žiaden komparátor} for i := 1 to poloziek do if komparatory[i][1] = 0 then {oddeľovač úrovní} prazdne stlpce(stlpec + 1, 2); {vykresli vodiče} vypis stav(stlpec + 3, sirka); {vypíš aktuálny stav} stlpec := stlpec sirka; novy stlpec := true; {začneme nový stĺpec komparátorov} end else {komparátor} if novy stlpec 14
15 or not je volno(komparatory[i][1], komparatory[i][2]) then {ak treba začať nový stĺpec komparátorov} prazdne stlpce(stlpec + 1, 3); {vykresli vodiče} for j := 1 to n do plne[j] := false; {inicializuj pole} stlpec := stlpec + 3; novy stlpec := false; {vykresli a simuluj komp., zapíš ho pola plne} spracuj komparator(komparatory[i][1], komparatory[i][2], stlpec); {for i} { vykresli } nacitaj; vykresli; readln; clrscr; end. {hlavný program} {načítaj vstup} {vykresli priebeh výpočtu siete} {počkaj na stlačenie klávesy enter} {zmaž obrazovku} 15
16 SLOVENSKÁ KOMISIA MATEMATICKEJ OLYMPIÁDY 51. ROČNÍK MATEMATICKEJ OLYMPIÁDY Leták kategórie P Vydala IUVENTA pre vnútornú potrebu Ministerstva školstva SR Autori príkladov B. Brejová, M. Forišek, M. Pál a T. Vinař Programom L A TEX sadzbu pripravili T. Vinař a B. Brejová c Slovenská komisia Matematickej olympiády, 2001
Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, prič
 Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, pričom to je veľmi dôležitá súčasť úlohy. Body sa udeľovali
Vzorové riešenia úlohy 4.1 Bodovanie Úvod do TI 2010 Dôvod prečo veľa z Vás malo málo bodov bolo to, že ste sa nepokúsili svoje tvrdenia dokázať, pričom to je veľmi dôležitá súčasť úlohy. Body sa udeľovali
Klasická metóda CPM
 Operačná analýza 2-02a Klasická metóda CPM Úvod Je daná úloha časového plánovania U s množinou elementárnych činností E a reálnou funkciou c: E R ktorá každej činnosti A E priradí jej dobu trvania c(a).
Operačná analýza 2-02a Klasická metóda CPM Úvod Je daná úloha časového plánovania U s množinou elementárnych činností E a reálnou funkciou c: E R ktorá každej činnosti A E priradí jej dobu trvania c(a).
SK MATEMATICKA OLYMPIADA 2010/ ročník MO Riešenia úloh domáceho kola kategórie Z4 1. Doplň do prázdnych políčok čísla od 1 do 7 každé raz tak,
 SK MATEMATICKA OLYMPIADA 2010/2011 60. ročník MO Riešenia úloh domáceho kola kategórie Z4 1. Doplň do prázdnych políčok čísla od 1 do 7 každé raz tak, aby matematické operácie boli vypočítané správne.
SK MATEMATICKA OLYMPIADA 2010/2011 60. ročník MO Riešenia úloh domáceho kola kategórie Z4 1. Doplň do prázdnych políčok čísla od 1 do 7 každé raz tak, aby matematické operácie boli vypočítané správne.
Microsoft Word - skripta3b.doc
 6. Vlastnosti binárnych relácií V tejto časti sa budeme venovať šiestim vlastnostiam binárnych relácií. Najprv si uvedieme ich definíciu. Reláciu R definovanú v množine M nazývame: a ) reflexívnou, ak
6. Vlastnosti binárnych relácií V tejto časti sa budeme venovať šiestim vlastnostiam binárnych relácií. Najprv si uvedieme ich definíciu. Reláciu R definovanú v množine M nazývame: a ) reflexívnou, ak
Paralelné algoritmy, cast c. 3
 Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Paralelné algoritmy, cast c. 2
 Paralelné algoritmy, čast č. 2 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 2 Paralelné algoritmy,
Paralelné algoritmy, čast č. 2 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2009/2010 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 2 Paralelné algoritmy,
Metódy násobenie v stredoveku
 1 Lucia Pekarčíková História matematiky Metódy násobenia v stredoveku (Referát) Lucia Pekarčíková 1.roč. II.stupňa Mat Inf ÚVOD V dobe ranného stredoveku sa v Európe všeobecne nepoužíval abakus, nerobili
1 Lucia Pekarčíková História matematiky Metódy násobenia v stredoveku (Referát) Lucia Pekarčíková 1.roč. II.stupňa Mat Inf ÚVOD V dobe ranného stredoveku sa v Európe všeobecne nepoužíval abakus, nerobili
STRUČNÝ NÁVOD KU IP-COACHU
 STRUČNÝ NÁVOD KU COACHU 6 Otvorenie programu a voľba úlohy na meranie Otvorenie programu Program COACH na meranie otvoríme kliknutím na ikonu Autor na obrazovke, potom zvolíme Užívateľskú úroveň Pokročilý
STRUČNÝ NÁVOD KU COACHU 6 Otvorenie programu a voľba úlohy na meranie Otvorenie programu Program COACH na meranie otvoríme kliknutím na ikonu Autor na obrazovke, potom zvolíme Užívateľskú úroveň Pokročilý
STRUČNÝ NÁVOD KU IP-COACHU
 STRUČNÝ NÁVOD KU COACHU 5 Otvorenie programu a voľba úlohy na meranie Otvorenie programu Program IP- COACH na meranie otvoríme kliknutím na ikonu na obrazovke: Obr.1 Voľba úlohy na meranie Po kliknutí
STRUČNÝ NÁVOD KU COACHU 5 Otvorenie programu a voľba úlohy na meranie Otvorenie programu Program IP- COACH na meranie otvoríme kliknutím na ikonu na obrazovke: Obr.1 Voľba úlohy na meranie Po kliknutí
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom
 2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
2.5. Dotyčnica krivky, dotykový kužeľ. Nech f je krivka a nech P V (f) (t.j. m P (f) 1). Ak m P (f) = r a l je taká priamka, že I P (f, l) > r, potom l nazývame dotyčnicou krivky f v bode P. Pre daný bod
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1.2 Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru
 8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
8 Cvičenie 1.1 Dokážte, že pre ľubovoľné body X, Y, Z platí X + Y Z = Z + Y X. 1. Dokážte, že pre ľubovoľné body A, B, D, E, F, G afinného priestoru P platí F B = F A, BD = AE, DG = EG F = G. 1.3 Dokážte
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/ ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných r
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 009/010 59. ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných reálnych čísel, ktoré sú riešením sústavy rovníc a b c
SK MATEMATICKÁOLYMPIÁDA skmo.sk 009/010 59. ročník MO Riešenia úloh česko-poľsko-slovenského stretnutia 1. Určte všetky trojice (a, b, c) kladných reálnych čísel, ktoré sú riešením sústavy rovníc a b c
Microsoft Word - 06b976f06a0Matice - Uzivatelska Dokumentacia
 Matice Užívateľská dokumentácia k programu Autor: Miroslav Jakubík 2009 Obsah 1 Úvod... 2 1.1 Stručný popis programu... 2 1.2 Spustenie programu... 2 1.3 Otvorenie dokumentu... 3 1.4 Ovládanie programu...
Matice Užívateľská dokumentácia k programu Autor: Miroslav Jakubík 2009 Obsah 1 Úvod... 2 1.1 Stručný popis programu... 2 1.2 Spustenie programu... 2 1.3 Otvorenie dokumentu... 3 1.4 Ovládanie programu...
Relačné a logické bázy dát
 Unifikácia riešenie rovníc v algebre termov Ján Šturc Zima, 2010 Termy a substitúcie Definícia (term): 1. Nech t 0,..., t n -1 sú termy a f je n-árny funkčný symbol, potom aj f(t 0,..., t n -1 ) je term.
Unifikácia riešenie rovníc v algebre termov Ján Šturc Zima, 2010 Termy a substitúcie Definícia (term): 1. Nech t 0,..., t n -1 sú termy a f je n-árny funkčný symbol, potom aj f(t 0,..., t n -1 ) je term.
Microsoft Word - Zaver.pisomka_januar2010.doc
 Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Písomná skúška z predmetu lgebra a diskrétna matematika konaná dňa.. 00. príklad. Dokážte metódou vymenovaním prípadov vlastnosť: Tretie mocniny celých čísel sú reprezentované celými číslami ktoré končia
Algoritmizácia a programovanie - Príkazy
 Algoritmizácia a programovanie Príkazy prof. Ing. Ján Terpák, CSc. Technická univerzita v Košiciach Fakulta baníctva, ekológie, riadenia a geotechnológíı Ústav riadenia a informatizácie výrobných procesov
Algoritmizácia a programovanie Príkazy prof. Ing. Ján Terpák, CSc. Technická univerzita v Košiciach Fakulta baníctva, ekológie, riadenia a geotechnológíı Ústav riadenia a informatizácie výrobných procesov
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 1. 3. marca 2006 2. 10. marca 2006 c RNDr. Monika Molnárová, PhD. Obsah 1 Aritmetické vektory a matice 4 1.1 Aritmetické vektory........................
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 1. 3. marca 2006 2. 10. marca 2006 c RNDr. Monika Molnárová, PhD. Obsah 1 Aritmetické vektory a matice 4 1.1 Aritmetické vektory........................
Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy
 Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy) alebo analyticky (výpočet súradníc bodov elipsy).
Metrické konštrukcie elipsy Soňa Kudličková, Alžbeta Mackovová Elipsu, ako regulárnu kužeľosečku, môžeme študovať synteticky (konštrukcie bodov elipsy) alebo analyticky (výpočet súradníc bodov elipsy).
Operačná analýza 2
 Súradnicové sústavy a zobrazenia Súradnicové sústavy v rovine (E 2 ) 1. Karteziánska súradnicová sústava najpoužívanejšia súradnicová sústava; určená začiatkom O, kolmými osami x, y a rovnakými jednotkami
Súradnicové sústavy a zobrazenia Súradnicové sústavy v rovine (E 2 ) 1. Karteziánska súradnicová sústava najpoužívanejšia súradnicová sústava; určená začiatkom O, kolmými osami x, y a rovnakými jednotkami
1 Rekurencie este raz riesenia niektorych rekurencii z cvik. mame danu rekurenciu napr T (n) = at ( n b ) + k. idea postupu je postupne rozpisovat cle
 1 Rekurencie este raz riesenia niektorych rekurencii z cvik. mame danu rekurenciu napr at b + k. idea postupu je postupne rozpisovat cleny T b... teda T b = at + 1... dokym v tom neuvidime nejaky tvar
1 Rekurencie este raz riesenia niektorych rekurencii z cvik. mame danu rekurenciu napr at b + k. idea postupu je postupne rozpisovat cleny T b... teda T b = at + 1... dokym v tom neuvidime nejaky tvar
Pokrocilé programovanie XI - Diagonalizácia matíc
 Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
Pokročilé programovanie XI Diagonalizácia matíc Peter Markoš Katedra experimentálnej fyziky F2-523 Letný semester 2015/2016 Obsah Fyzikálne príklady: zviazané oscilátory, anizotrópne systémy, kvantová
M59dkZ9ri10
 MATEMATICKÁ OLYMPIÁDA Komentáre a riešenia úloh domáceho kola pre žiakov základných škôl a nižších ročníkov osemročných gymnázií Kategória Z9 59 ročník Školský rok 2009/2010 KATEGÓRIA Z9 Z9 I 1 Dostal
MATEMATICKÁ OLYMPIÁDA Komentáre a riešenia úloh domáceho kola pre žiakov základných škôl a nižších ročníkov osemročných gymnázií Kategória Z9 59 ročník Školský rok 2009/2010 KATEGÓRIA Z9 Z9 I 1 Dostal
Informačné technológie
 Informačné technológie Piatok 15.11. 2013 Matúš Péči Barbora Zahradníková Soňa Duchovičová Matúš Gramlička Začiatok/Koniec Z K Vstup/Výstup A, B Načítanie vstupných premenných A, B resp. výstup výstupných
Informačné technológie Piatok 15.11. 2013 Matúš Péči Barbora Zahradníková Soňa Duchovičová Matúš Gramlička Začiatok/Koniec Z K Vstup/Výstup A, B Načítanie vstupných premenných A, B resp. výstup výstupných
Microsoft Word - 6 Výrazy a vzorce.doc
 6 téma: Výrazy a vzorce I Úlohy na úvod 1 1 Zistite definičný obor výrazu V = 4 Riešte sústavu 15 = 6a + b, = 4a c, 1 = 4a + b 16c Rozložte na súčin výrazy a) b 4 a 18, b) c 5cd 10c d +, c) 6 1 s + z 4
6 téma: Výrazy a vzorce I Úlohy na úvod 1 1 Zistite definičný obor výrazu V = 4 Riešte sústavu 15 = 6a + b, = 4a c, 1 = 4a + b 16c Rozložte na súčin výrazy a) b 4 a 18, b) c 5cd 10c d +, c) 6 1 s + z 4
Ďalšie vlastnosti goniometrických funkcií
 Ďalšie vlastnosti goniometrických funkcií Na obrázku máme bod B na jednotkovej kružnici, a rovnobežne s y-ovou osou bodom B vznikol pravouhlý trojuholník. Jeho prepona je polomer kružnice má veľkosť 1,
Ďalšie vlastnosti goniometrických funkcií Na obrázku máme bod B na jednotkovej kružnici, a rovnobežne s y-ovou osou bodom B vznikol pravouhlý trojuholník. Jeho prepona je polomer kružnice má veľkosť 1,
prijimacky 2014 MAT 4rocne ver A.doc
 Priezvisko a meno: " Sem nepíš! Kód: M-A-4r Kód: M-A-4r 1. súkromné gymnázium v Bratislave, Bajkalská 20, Bratislava Test z matematiky (verzia A 12. máj 2014) Pokyny pre žiakov 1. 2. Tento test obsahuje
Priezvisko a meno: " Sem nepíš! Kód: M-A-4r Kód: M-A-4r 1. súkromné gymnázium v Bratislave, Bajkalská 20, Bratislava Test z matematiky (verzia A 12. máj 2014) Pokyny pre žiakov 1. 2. Tento test obsahuje
Paralelné algoritmy, cast c. 3
 Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2011/2012 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Paralelné algoritmy, čast č. 3 František Mráz Kabinet software a výuky informatiky, MFF UK, Praha Paralelné algoritmy, 2011/2012 František Mráz (KSVI MFF UK) Paralelné algoritmy, čast č. 3 Paralelné algoritmy,
Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovsk
 Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovská cesta 1, 034 01 Ružomberok, Slovakia e-mail: marian.trenkler@ku.sk
Zeszyty Naukowe PWSZ, Nowy Sącz 2013 Konštrukcie magických obdĺžnikov Marián Trenkler Faculty of Education, Catholic University in Ružomberok Hrabovská cesta 1, 034 01 Ružomberok, Slovakia e-mail: marian.trenkler@ku.sk
Centrum vedecko-technických informácií, Odbor pre hodnotenie vedy, Oddelenie pre hodnotenie publikačnej činnosti Vyhľadávanie a práca so záznamami - C
 Centrum vedecko-technických informácií, Odbor pre hodnotenie vedy, Oddelenie pre hodnotenie publikačnej činnosti Vyhľadávanie a práca so záznamami - CREPČ 2 Manuál pre autorov (aktualizované dňa 18.3.2019)
Centrum vedecko-technických informácií, Odbor pre hodnotenie vedy, Oddelenie pre hodnotenie publikačnej činnosti Vyhľadávanie a práca so záznamami - CREPČ 2 Manuál pre autorov (aktualizované dňa 18.3.2019)
Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Pra
 Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Praktické programovanie assemblerových funkcií Autor:
Úroveň strojového kódu procesor Intel Pentium Pamäťový operand Adresovanie pamäte Priama nepriama a indexovaná adresa Práca s jednorozmerným poľom Praktické programovanie assemblerových funkcií Autor:
Algoritmizácia a programovanie - Štruktúrované údajové typy
 Algoritmizácia a programovanie Štruktúrované údajové typy prof. Ing. Ján Terpák, CSc. Technická univerzita v Košiciach Fakulta baníctva, ekológie, riadenia a geotechnológíı Ústav riadenia a informatizácie
Algoritmizácia a programovanie Štruktúrované údajové typy prof. Ing. Ján Terpák, CSc. Technická univerzita v Košiciach Fakulta baníctva, ekológie, riadenia a geotechnológíı Ústav riadenia a informatizácie
Pracovný postup pre vypĺňanie údajov elektronického formulára IŠIS pre spravodajskú jednotku 1
 Pracovný postup pre vypĺňanie údajov elektronického formulára IŠIS pre spravodajskú jednotku 1 Prihláste sa do aplikácie pomocou prihlasovacích údajov pre spravodajskú jednotku. Link na aplikáciu: http://isis.statistics.sk/
Pracovný postup pre vypĺňanie údajov elektronického formulára IŠIS pre spravodajskú jednotku 1 Prihláste sa do aplikácie pomocou prihlasovacích údajov pre spravodajskú jednotku. Link na aplikáciu: http://isis.statistics.sk/
midterm2014_1
 Midterm 2014 Meno a priezvisko: obsahuje 5 príkladov, spolu 31>25 bodov skupina: 1) [8 bodov] Zistite, čo počíta nasledujúca funkcia foo pre n>=0. Hint: foo(1000) = 1. static long foo(long n) { return
Midterm 2014 Meno a priezvisko: obsahuje 5 príkladov, spolu 31>25 bodov skupina: 1) [8 bodov] Zistite, čo počíta nasledujúca funkcia foo pre n>=0. Hint: foo(1000) = 1. static long foo(long n) { return
(ıkolské kolo-PYT)
 Súťažné úlohy školského kola. Školský rok 2006/2007. Kategória P 3 1. Súčet dvoch čísel je 156. Prvý sčítanec je rozdiel čísel 86 a 34. Aký je druhý sčítanec? 2. Vypočítaj: 19 18 + 17 16 + 15 14 = 3. V
Súťažné úlohy školského kola. Školský rok 2006/2007. Kategória P 3 1. Súčet dvoch čísel je 156. Prvý sčítanec je rozdiel čísel 86 a 34. Aký je druhý sčítanec? 2. Vypočítaj: 19 18 + 17 16 + 15 14 = 3. V
Microsoft Word - mnohouholnik.doc
 Výpočet obsahu mnohouholníka Mnohouholník je daný súradnicami svojich vrcholov: A1[x1, y1], A2[x2, y2],..., An[xn, yn]. Aby sme sa vyhli komplikáciám, obmedzíme sa na prípad konvexného mnohouholníka. Súradnice
Výpočet obsahu mnohouholníka Mnohouholník je daný súradnicami svojich vrcholov: A1[x1, y1], A2[x2, y2],..., An[xn, yn]. Aby sme sa vyhli komplikáciám, obmedzíme sa na prípad konvexného mnohouholníka. Súradnice
Microsoft Word - zapis-predmetov-AiS
 Zápis predmetov do AiS na aktuálny akademický rok Pred zápisom predmetov Vám odporúčame pozorne si prečítať študijný plán pre Váš študijný program. Môžete si ho zobraziť v AiSe kliknutím na "Študijné programy"
Zápis predmetov do AiS na aktuálny akademický rok Pred zápisom predmetov Vám odporúčame pozorne si prečítať študijný plán pre Váš študijný program. Môžete si ho zobraziť v AiSe kliknutím na "Študijné programy"
Snímka 1
 Generovanie LOGICKÝCH KONJUNKCIÍ doc. Ing. Kristína Machová, PhD. kristina.machova@tuke.sk http://people.tuke.sk/kristina.machova/ OSNOVA: 1. Prehľadávanie priestoru pojmov 2. Reprezentácia a použitie
Generovanie LOGICKÝCH KONJUNKCIÍ doc. Ing. Kristína Machová, PhD. kristina.machova@tuke.sk http://people.tuke.sk/kristina.machova/ OSNOVA: 1. Prehľadávanie priestoru pojmov 2. Reprezentácia a použitie
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú in
 Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Metódy dokazovanie v matematike 1 Základné pojmy Matematika exaktná veda vybudovaná DEDUKTÍVNE ZÁKLADNÉ POJMY základy každej matematickej teórie sú intuitívne jasné a názorné napr. prirodzené čísla, zlomok,
Kolmogorovská zložitost
 Kolmogorovská zložitosť 5.12.2013 (2013/14) KZ 5.12.2013 1 / 16 Kt zložitosť age(x) = min p{2 l(p) t : U(p) = x v priebehu t krokov} Def. (Kt zložitosť) UTS monotonne skenuje začiatok p kým vypíše x, t(p,
Kolmogorovská zložitosť 5.12.2013 (2013/14) KZ 5.12.2013 1 / 16 Kt zložitosť age(x) = min p{2 l(p) t : U(p) = x v priebehu t krokov} Def. (Kt zložitosť) UTS monotonne skenuje začiatok p kým vypíše x, t(p,
Microsoft Word - Argumentation_presentation.doc
 ARGUMENTÁCIA V. Kvasnička Ústav aplikovanej informatiky FIIT STU Seminár UI, dňa 21.11.2008 Priesvitka 1 Úvodné poznámky Argumentácia patrí medzi dôležité aspekty ľudskej inteligencie. Integrálnou súčasťou
ARGUMENTÁCIA V. Kvasnička Ústav aplikovanej informatiky FIIT STU Seminár UI, dňa 21.11.2008 Priesvitka 1 Úvodné poznámky Argumentácia patrí medzi dôležité aspekty ľudskej inteligencie. Integrálnou súčasťou
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) Matematická analýza IV (ÚMV/MAN2d/10) RNDr. Lenka Halčinová, PhD.
 III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
III. Diferenciálny počet funkcie viac premenných (Prezentácia k prednáškam, čast B) (ÚMV/MAN2d/10) lenka.halcinova@upjs.sk 11. apríla 2019 3.3 Derivácia v smere, vzt ah diferenciálu, gradientu a smerovej
MATEMATICKÁ OLYMPIÁDA NA STREDNÝCH ŠKOLÁCH 54. ročník, školský rok 2004/2005 Zadania úloh 3. kola kategórie P 1. súťažný deň Na riešenie úloh máte 4.5
 MATEMATICKÁ OLYMPIÁDA NA STREDNÝCH ŠKOLÁCH 54. ročník, školský rok 2004/2005 Zadania úloh 3. kola kategórie P 1. súťažný deň Na riešenie úloh máte 4.5 hodiny čistého času. Riešenie každého príkladu musí
MATEMATICKÁ OLYMPIÁDA NA STREDNÝCH ŠKOLÁCH 54. ročník, školský rok 2004/2005 Zadania úloh 3. kola kategórie P 1. súťažný deň Na riešenie úloh máte 4.5 hodiny čistého času. Riešenie každého príkladu musí
Preco kocka stací? - o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, ked sú velké
 o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké o tom, ako sú rozdelené vlastné hodnoty laplasiánu v limite, keď sú veľké zaujímavé, ale len pre matematikov... NIE! o tom, ako
Microsoft Word - Priloha_1.docx
 Obsah 1 Úvod... 1 2 Hlavné menu verejnej časti ITMS2014+... 1 3 Zoznam ŽoNFP na verejnej časti ITMS2014+... 2 3.1 Vyhľadávanie ŽoNFP... 2 3.2 Horná lišta zoznamu ŽoNFP... 2 3.3 Stĺpce zoznamu ŽoNFP...
Obsah 1 Úvod... 1 2 Hlavné menu verejnej časti ITMS2014+... 1 3 Zoznam ŽoNFP na verejnej časti ITMS2014+... 2 3.1 Vyhľadávanie ŽoNFP... 2 3.2 Horná lišta zoznamu ŽoNFP... 2 3.3 Stĺpce zoznamu ŽoNFP...
NÁVRH UČEBNÝCH OSNOV PRE 1
 PROGRAMOVANIE UČEBNÉ OSNOVY do ŠkVP Charakteristika voliteľného učebného predmetu Programovanie Programovanie rozširuje a prehlbuje žiacke vedomosti z predchádzajúcich povinného predmetu Informatika. Kompetencie
PROGRAMOVANIE UČEBNÉ OSNOVY do ŠkVP Charakteristika voliteľného učebného predmetu Programovanie Programovanie rozširuje a prehlbuje žiacke vedomosti z predchádzajúcich povinného predmetu Informatika. Kompetencie
N desitka.indd
 DESIATKA Interakčná, taktická kartová hra od holandských autorov. Hra, v ktorej sa snažíte prekabátiť svojich súperov! Hra, v ktorej môže zvíťaziť aj ten, komu šťastie práve nepraje. Podmienkou sú pevné
DESIATKA Interakčná, taktická kartová hra od holandských autorov. Hra, v ktorej sa snažíte prekabátiť svojich súperov! Hra, v ktorej môže zvíťaziť aj ten, komu šťastie práve nepraje. Podmienkou sú pevné
Matematický model činnosti sekvenčného obvodu 7 MATEMATICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčnéh
 7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
7 MTEMTICKÝ MODEL ČINNOSTI SEKVENČNÉHO OBVODU Konečný automat predstavuje matematický model sekvenčného obvodu. Konečný automat je usporiadaná pätica = (X, S, Y, δ, λ,) (7.) kde X je konečná neprázdna
Microsoft Word - prirucka_katedry_nova
 Práca v systéme BUXUS Príručka pre katedrových redaktorov Michal Minarik michal.minarik@stuba.sk 2 Obsah Prihlásenie do systému BUXUS... 3 Prihlasovacie údaje... 3 Prihlasovacia obrazovka... 3 Úvodné menu...
Práca v systéme BUXUS Príručka pre katedrových redaktorov Michal Minarik michal.minarik@stuba.sk 2 Obsah Prihlásenie do systému BUXUS... 3 Prihlasovacie údaje... 3 Prihlasovacia obrazovka... 3 Úvodné menu...
(Microsoft Word - Tuzemsk\341 a zahrani\350n\341 jazda \232tandardn\341 jazda.docx)
 Vytvorenie tuzemskej a zahraničnej jazdy, štandardná jazda V postupe sú uvedené kroky, ktorými môžeme rýchlo a jednoducho vytvoriť ďalšie jazdy a cestovné príkazy pomocou štandardných jázd. Tuzemská jazda
Vytvorenie tuzemskej a zahraničnej jazdy, štandardná jazda V postupe sú uvedené kroky, ktorými môžeme rýchlo a jednoducho vytvoriť ďalšie jazdy a cestovné príkazy pomocou štandardných jázd. Tuzemská jazda
enum
 Objektovo orientované programovanie (enumeračné typy) 8. prednáška (3. časť) Vladislav Novák FEI STU v Bratislave 4.11.2014 (úprava 10.11. na str. 1, 3, 5) Enumeračné typy (Vymenované typy) Enumeračný
Objektovo orientované programovanie (enumeračné typy) 8. prednáška (3. časť) Vladislav Novák FEI STU v Bratislave 4.11.2014 (úprava 10.11. na str. 1, 3, 5) Enumeračné typy (Vymenované typy) Enumeračný
Siete vytvorené z korelácií casových radov
 Siete vytvorené z korelácií časových radov Beáta Stehlíková 2-EFM-155 Analýza sociálnych sietí Fakulta matematiky, fyziky a informatiky, UK v Bratislave, 2019 Siete vytvorené z korelácií Siete vytvorené
Siete vytvorené z korelácií časových radov Beáta Stehlíková 2-EFM-155 Analýza sociálnych sietí Fakulta matematiky, fyziky a informatiky, UK v Bratislave, 2019 Siete vytvorené z korelácií Siete vytvorené
Microsoft Word - Diskusia11.doc
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky MATEMATIKA - 011 sem vlepiť čiarový kód uchádzača Test obsahuje 30 úloh. Na jeho vypracovanie máte 90 minút. Každá úloha spolu
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky MATEMATIKA - 011 sem vlepiť čiarový kód uchádzača Test obsahuje 30 úloh. Na jeho vypracovanie máte 90 minút. Každá úloha spolu
Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 2017 Definície Žena - objekt ohodnotený celým číslom. Každé dve ženy sa dajú porovnat a
 Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 207 Definície Žena - objekt ohodnotený celým číslom. aždé dve ženy sa dajú porovnat a rozlíšit, t.j. žiadne dve nemajú rovanké hodnotenie.
Aplikace matematiky- záverečná práca Juraj Bodík 28. septembra 207 Definície Žena - objekt ohodnotený celým číslom. aždé dve ženy sa dajú porovnat a rozlíšit, t.j. žiadne dve nemajú rovanké hodnotenie.
História
 Fakulta riadenia a informatiky ŽU Množiny Pojmy zavedené v 8. prednáške N-rozmerné polia Dvojrozmerné polia matica definícia typ[][] premenna inicializácia new typ[pocetriadkov][pocetstlpcov] práca s prvkami
Fakulta riadenia a informatiky ŽU Množiny Pojmy zavedené v 8. prednáške N-rozmerné polia Dvojrozmerné polia matica definícia typ[][] premenna inicializácia new typ[pocetriadkov][pocetstlpcov] práca s prvkami
Informačný systém pre externú časť a písomnú formu internej časti maturitnej skúšky Informačný systém pre EČ a PFIČ maturitnej skúšky Užívateľská prír
 Informačný systém pre EČ a PFIČ maturitnej skúšky Užívateľská príručka pre opravný termín EČ a PFIČ Máj 2019 Obsah 1. ZÁKLADNÉ POKYNY... 3 2. ÚDAJE O ŠKOLE... 4 2.1 KONTROLA A ZMENA ÚDAJOV... 4 2.2 ZMENA
Informačný systém pre EČ a PFIČ maturitnej skúšky Užívateľská príručka pre opravný termín EČ a PFIČ Máj 2019 Obsah 1. ZÁKLADNÉ POKYNY... 3 2. ÚDAJE O ŠKOLE... 4 2.1 KONTROLA A ZMENA ÚDAJOV... 4 2.2 ZMENA
Priebeh funkcie
 Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
Technická univerzita Košice monika.molnarova@tuke.sk Obsah 1 Monotónnosť funkcie Lokálne extrémy funkcie Globálne (absolútne) extrémy funkcie Konvexnosť a konkávnosť funkcie Monotónnosť funkcie Monotónnosť
Snímka 1
 Mgr. Ing. Roman Horváth, PhD. Katedra matematiky a informatiky Pedagogická fakulta Trnavská univerzita v Trnave roman.horvath@truni.sk Algoritmus a vlastnosti algoritmov Algoritmus konečná postupnosť krokov
Mgr. Ing. Roman Horváth, PhD. Katedra matematiky a informatiky Pedagogická fakulta Trnavská univerzita v Trnave roman.horvath@truni.sk Algoritmus a vlastnosti algoritmov Algoritmus konečná postupnosť krokov
1)
 Prijímacia skúška z matematiky do prímy gymnázia s osemročným štúdiom Milá žiačka/milý žiak, sme veľmi radi, že ste sa rozhodli podať prihlášku na našu školu. Dúfame, že nasledujúce úlohy hravo vyriešite
Prijímacia skúška z matematiky do prímy gymnázia s osemročným štúdiom Milá žiačka/milý žiak, sme veľmi radi, že ste sa rozhodli podať prihlášku na našu školu. Dúfame, že nasledujúce úlohy hravo vyriešite
MERANIE U a I.doc
 MERANIE ELEKTRICKÉHO NAPÄTIA A ELEKTRICKÉHO PRÚDU Teoretický úvod: Základnými prístrojmi na meranie elektrických veličín sú ampérmeter na meranie prúdu a voltmeter na meranie napätia. Univerzálne meracie
MERANIE ELEKTRICKÉHO NAPÄTIA A ELEKTRICKÉHO PRÚDU Teoretický úvod: Základnými prístrojmi na meranie elektrických veličín sú ampérmeter na meranie prúdu a voltmeter na meranie napätia. Univerzálne meracie
PowerPoint Presentation
 Seminár Robotika.SK Ako naučiť robota vidieť ľudskú tvár pomocou knižnice Dlib Andrej Lúčny Katedra aplikovanej informatiky FMFI UK lucny@fmph.uniba.sk http://dai.fmph.uniba.sk/w/andrej_lucny www.robotika.sk/cviko7-faces.zip
Seminár Robotika.SK Ako naučiť robota vidieť ľudskú tvár pomocou knižnice Dlib Andrej Lúčny Katedra aplikovanej informatiky FMFI UK lucny@fmph.uniba.sk http://dai.fmph.uniba.sk/w/andrej_lucny www.robotika.sk/cviko7-faces.zip
Navigácia po úvodnej stránke elektronickej schránky Dátum zverejnenia: Verzia: 10 Dátum aktualizácie: Navigácia po úvodnej st
 Navigácia po úvodnej stránke elektronickej schránky UPOZORNENIE: Od 1. 1. 2019 sa mení názov odosielateľa správ z Úrad vlády Slovenskej republiky ÚPVS na Ústredný portál verejnej správy. Zoznam zmien:
Navigácia po úvodnej stránke elektronickej schránky UPOZORNENIE: Od 1. 1. 2019 sa mení názov odosielateľa správ z Úrad vlády Slovenskej republiky ÚPVS na Ústredný portál verejnej správy. Zoznam zmien:
Prihlásenie sa do systému AIS2 Pomôcka pre študentov Odoslanie záverečnej práce cez AiS2 Spustite si internetový prehliadač a do riadku s adresou napí
 Prihlásenie sa do systému AIS2 Pomôcka pre študentov Odoslanie záverečnej práce cez AiS2 Spustite si internetový prehliadač a do riadku s adresou napíšte https://ais2.umb.sk. Do systému AIS2 sa prihlasujete
Prihlásenie sa do systému AIS2 Pomôcka pre študentov Odoslanie záverečnej práce cez AiS2 Spustite si internetový prehliadač a do riadku s adresou napíšte https://ais2.umb.sk. Do systému AIS2 sa prihlasujete
Agenda záverečnej práce pedagóg Celá agenda týkajúca sa záverečnej práce je dostupná v obrazovke Záverečná práca (menu Agenda pedagóga -> Záverečné pr
 Agenda záverečnej práce pedagóg Celá agenda týkajúca sa záverečnej práce je dostupná v obrazovke Záverečná práca (menu Agenda pedagóga -> Záverečné práce). ZP1 odovzdanie záverečnej práce blok je prístupný
Agenda záverečnej práce pedagóg Celá agenda týkajúca sa záverečnej práce je dostupná v obrazovke Záverečná práca (menu Agenda pedagóga -> Záverečné práce). ZP1 odovzdanie záverečnej práce blok je prístupný
Pokrocilé spracovanie obrazu - Fourierová transformácia
 Pokročilé spracovanie obrazu - Fourierová transformácia Ing. Viktor Kocur viktor.kocur@fmph.uniba.sk DAI FMFI UK 29.11.2017 Obsah 1 Segmentácia O čo ide 2 Watershed Princíp Postup 3 k-means clustering
Pokročilé spracovanie obrazu - Fourierová transformácia Ing. Viktor Kocur viktor.kocur@fmph.uniba.sk DAI FMFI UK 29.11.2017 Obsah 1 Segmentácia O čo ide 2 Watershed Princíp Postup 3 k-means clustering
SK MATEMATICKÁOLYMPIÁDA skmo.sk 64. ročník Matematickej olympiády 2014/2015 Riešenia úloh domáceho kola kategórie Z8 1. Písmenkový logik je hra pre dv
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 64. ročník Matematickej olympiády 2014/2015 Riešenia úloh domáceho kola kategórie Z8 1. Písmenkový logik je hra pre dvoch hráčov, ktorá má nasledujúce pravidlá: 1. Prvý
SK MATEMATICKÁOLYMPIÁDA skmo.sk 64. ročník Matematickej olympiády 2014/2015 Riešenia úloh domáceho kola kategórie Z8 1. Písmenkový logik je hra pre dvoch hráčov, ktorá má nasledujúce pravidlá: 1. Prvý
Microsoft Word - Príloha P2 - zadania pracovných listov pre 6. ročník
 P1 zadania pracovných listov pre 6. ročník 6.ročník, PL-1A (vstupný) 1. Vytvorte všetky trojciferné čísla z číslic 1, 2, 7, 0. 2. Sú dané veľkosti uhlov: 23, 37, 49, 89,112, 90, 147, 152, 176. Rozdeľte
P1 zadania pracovných listov pre 6. ročník 6.ročník, PL-1A (vstupný) 1. Vytvorte všetky trojciferné čísla z číslic 1, 2, 7, 0. 2. Sú dané veľkosti uhlov: 23, 37, 49, 89,112, 90, 147, 152, 176. Rozdeľte
Microsoft Word - Transparencies03.doc
 3. prednáška Teória množín II relácie o operácie nad reláciami o rovnosť o usporiadanosť funkcie o zložená funkcia o inverzná funkcia. Verzia: 20. 3. 2006 Priesvitka: 1 Relácie Definícia. Nech X a Y sú
3. prednáška Teória množín II relácie o operácie nad reláciami o rovnosť o usporiadanosť funkcie o zložená funkcia o inverzná funkcia. Verzia: 20. 3. 2006 Priesvitka: 1 Relácie Definícia. Nech X a Y sú
gameDescription_bigApple
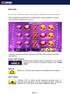
 Big Apple Big Apple Popis a pravidlá Big Apple je hra s troma kotúčmi. Výsledky hry tvoria 3 3 výsledky, pričom každý kotúč zobrazuje časť s troma symbolmi. Snímky obrazovky Nasledujúci obrázok zobrazuje
Big Apple Big Apple Popis a pravidlá Big Apple je hra s troma kotúčmi. Výsledky hry tvoria 3 3 výsledky, pričom každý kotúč zobrazuje časť s troma symbolmi. Snímky obrazovky Nasledujúci obrázok zobrazuje
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/ ročník Matematickej olympiády Riešenia úloh IMO 1. Určte všetky funkcie f: R R také, že rovnosť f ( x y
 SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/2010 59. ročník Matematickej olympiády Riešenia úloh IMO 1. Určte všetky funkcie f: R R také, že rovnosť f ( x y ) = f(x) f(y) platí pre všetky x, y R. (Symbol z označuje
SK MATEMATICKÁOLYMPIÁDA skmo.sk 2009/2010 59. ročník Matematickej olympiády Riešenia úloh IMO 1. Určte všetky funkcie f: R R také, že rovnosť f ( x y ) = f(x) f(y) platí pre všetky x, y R. (Symbol z označuje
Tabuľky_teoria
 Tabuľky v programe Microsoft Word Vytvorenie tabuľky Pred samotným vyhotovením tabuľky sa odporúča pripraviť si náčrt, na ktorom sa rozvrhne rozdelenie údajov do riadkov a stĺpcov. Tabuľku vytvoríme pomocou
Tabuľky v programe Microsoft Word Vytvorenie tabuľky Pred samotným vyhotovením tabuľky sa odporúča pripraviť si náčrt, na ktorom sa rozvrhne rozdelenie údajov do riadkov a stĺpcov. Tabuľku vytvoríme pomocou
Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. Katedra matematických metód, Fa
 Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. stefan.pesko@fri.uniza.sk Katedra matematických metód, Fakulta riadenia a informatiky, Žilinská univerzita v
Podpora metód operačného výskumu pri navrhovaní systému liniek doc. RNDr. Štefan PEŠKO, CSc. stefan.pesko@fri.uniza.sk Katedra matematických metód, Fakulta riadenia a informatiky, Žilinská univerzita v
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Katedra informatiky PLATNOSŤ BERGE-FULKERSONOVEJ HYPOTÉZY PRE ŠPECIÁLNE TR
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Katedra informatiky PLATNOSŤ BERGE-FULKERSONOVEJ HYPOTÉZY PRE ŠPECIÁLNE TRIEDY SNARKOV Peter Gazdík DIPLOMOVÁ PRÁCA Vedúci diplomovej
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Katedra informatiky PLATNOSŤ BERGE-FULKERSONOVEJ HYPOTÉZY PRE ŠPECIÁLNE TRIEDY SNARKOV Peter Gazdík DIPLOMOVÁ PRÁCA Vedúci diplomovej
Identity Lifecycle Management
 4. prednáška (7.3.2016) Stromy alebo rodostromy a tajomstvá TreeSet-u 1 Hierarchie okolo nás Stromové zobrazenie adresárovej štruktúry Hierarchický diagram 2 Strom potomkov Janko Janko má deti Jožka, Máriu
4. prednáška (7.3.2016) Stromy alebo rodostromy a tajomstvá TreeSet-u 1 Hierarchie okolo nás Stromové zobrazenie adresárovej štruktúry Hierarchický diagram 2 Strom potomkov Janko Janko má deti Jožka, Máriu
Detail správy a súvisiace prvky Dátum zverejnenia: Verzia: 5 Dátum aktualizácie: Detail správy a súvisiace prvky UPOZORNENIE
 UPOZORNENIE: Od 1. 1. 2019 sa mení názov odosielateľa správ z Úrad vlády Slovenskej republiky ÚPVS na Ústredný portál verejnej správy. Zoznam zmien: Dátum vydania Verzia Popis zmien 31. 12. 2018 2 Str.
UPOZORNENIE: Od 1. 1. 2019 sa mení názov odosielateľa správ z Úrad vlády Slovenskej republiky ÚPVS na Ústredný portál verejnej správy. Zoznam zmien: Dátum vydania Verzia Popis zmien 31. 12. 2018 2 Str.
Analýza sociálnych sietí Geografická lokalizácia krajín EU
 Analýza sociálnych sietí Geografická lokalizácia krajín EU Ekonomická fakulta TU v Košiciach 20. februára 2009 Vzt ahy medzi krajinami - teória grafov Doterajšie riešenia 1 problém farbenia grafov (Francis
Analýza sociálnych sietí Geografická lokalizácia krajín EU Ekonomická fakulta TU v Košiciach 20. februára 2009 Vzt ahy medzi krajinami - teória grafov Doterajšie riešenia 1 problém farbenia grafov (Francis
SK MATEMATICKÁOLYMPIÁDA skmo.sk 66. ročník Matematickej olympiády 2016/2017 Riešenia úloh domáceho kola kategórie Z9 1. Vo všetkých deviatich políčkac
 SK MTEMTIKÁOLYMPIÁD skmo.sk 66. ročník Matematickej olympiády 2016/2017 Riešenia úloh domáceho kola kategórie Z9 1. Vo všetkých deviatich políčkach útvaru majú byť vyplnené prirodzené čísla tak, aby platilo:
SK MTEMTIKÁOLYMPIÁD skmo.sk 66. ročník Matematickej olympiády 2016/2017 Riešenia úloh domáceho kola kategórie Z9 1. Vo všetkých deviatich políčkach útvaru majú byť vyplnené prirodzené čísla tak, aby platilo:
Programátorské etudy - Pascal
 MODIFIKÁCIA OBRÁZKOV ÚLOHA NA HODINU Dorobte projekt Modifikácia obrázkov, ktorý je zameraný na prácu s grafickou plochou ako dvojrozmerným poľom. Modifikáciu 13 máte predpripravenú. Doprogramujte ďalšie
MODIFIKÁCIA OBRÁZKOV ÚLOHA NA HODINU Dorobte projekt Modifikácia obrázkov, ktorý je zameraný na prácu s grafickou plochou ako dvojrozmerným poľom. Modifikáciu 13 máte predpripravenú. Doprogramujte ďalšie
1. KOMPLEXNÉ ČÍSLA 1. Nájdite výsledok operácie v tvare x+yi, kde x, y R. a i (5 2i)(4 i) b. i(1 + i)(1 i)(1 + 2i)(1 2i) (1 7i) c. (2+3i) a+bi d
 KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
KOMPLEXNÉ ČÍSLA Nájdite výsledok operácie v tvare xyi, kde x, y R 7i (5 i)( i) i( i)( i)( i)( i) ( 7i) (i) abi a bi, a, b R i(i) 5i Nájdite x, y R také, e (x y) i(x y) = i (ix y)(x iy) = i y ix x iy i
Slovenská technická univerzita v Bratislave Fakulta informatiky a informačných technológií Ilkovičova 2, , Bratislava 4 Internet vecí v našich ž
 Slovenská technická univerzita v Bratislave Fakulta informatiky a informačných technológií Ilkovičova 2, 842 16, Bratislava 4 Internet vecí v našich životoch [IoT] Používateľská príručka - Android Tím:
Slovenská technická univerzita v Bratislave Fakulta informatiky a informačných technológií Ilkovičova 2, 842 16, Bratislava 4 Internet vecí v našich životoch [IoT] Používateľská príručka - Android Tím:
midterm2019
 Midterm 2019 Meno a priezvisko: obsahuje 5 príkladov, spolu 6+5+5+5+6 = 27 bodov 1) [6 bodov] Prvočíselný Prvočísel je nekonečne veľa, elegantný Euklidov dôkaz sporom hovorí: Ak by ich bolo konečne veľa,
Midterm 2019 Meno a priezvisko: obsahuje 5 príkladov, spolu 6+5+5+5+6 = 27 bodov 1) [6 bodov] Prvočíselný Prvočísel je nekonečne veľa, elegantný Euklidov dôkaz sporom hovorí: Ak by ich bolo konečne veľa,
Informačná a modelová podpora pre kvantifikáciu prvkov daňovej sústavy SR
 Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Nelineárne optimalizačné modely a metódy Téma prednášky č. 5 Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie Ekonomická univerzita Dolnozemská 1 852 35 Bratislava Označme ako množinu
Resolution
 Nastavenie rozlíšenia obrazovky Kvôli podstate technológie displeja z tekutých kryštálov (LCD) je rozlíšenie obrazu vždy pevne stanovené. Najlepší výkon zobrazenia dosiahnete nastavením rozlíšenia obrazovky
Nastavenie rozlíšenia obrazovky Kvôli podstate technológie displeja z tekutých kryštálov (LCD) je rozlíšenie obrazu vždy pevne stanovené. Najlepší výkon zobrazenia dosiahnete nastavením rozlíšenia obrazovky
Operačná analýza 2
 Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
Krivky (čiary) Krivku môžeme definovať: trajektória (dráha) pohybujúceho sa bodu, jednoparametrická sústava bodov charakterizovaná určitou vlastnosťou,... Krivky môžeme deliť z viacerých hľadísk, napr.:
PowerPoint-Präsentation
 Global Payment Plus - phototan Návod na prechod z USB tokenu na phototan Vážení užívatelia, tento návod Vás prevedie niekoľkými jednoduchými krokmi nutnými pre úspešný prechod z USB tokenu na phototan.
Global Payment Plus - phototan Návod na prechod z USB tokenu na phototan Vážení užívatelia, tento návod Vás prevedie niekoľkými jednoduchými krokmi nutnými pre úspešný prechod z USB tokenu na phototan.
Inteligentné rozhodovacie systémy Heuristické prehľadávanie SP Október, 2018 Katedra kybernetiky
 Inteligentné rozhodovacie systémy Heuristické prehľadávanie SP Marian.Mach@tuke.sk http://people.tuke.sk/marian.mach Október, 2018 Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach 1 Best-first
Inteligentné rozhodovacie systémy Heuristické prehľadávanie SP Marian.Mach@tuke.sk http://people.tuke.sk/marian.mach Október, 2018 Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach 1 Best-first
Prenosový kanál a jeho kapacita
 Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Prenosový kanál a jeho kapacita Stanislav Palúch Fakulta riadenia a informatiky, Žilinská univerzita 5. mája 2011 Stanislav Palúch, Fakulta riadenia a informatiky, Žilinská univerzita Prenosový kanál a
Fotonávod na vymeranie a objednanie horizontálnej žalúzie na retiazku 1. Vymeranie šírky a výšky horizontálnej žalúzie na retiazku - vymeranie sa vyko
 Fotonávod na vymeranie a objednanie horizontálnej žalúzie na retiazku 1. Vymeranie šírky a výšky horizontálnej žalúzie na retiazku - vymeranie sa vykonáva podľa uchytenia. Nižšie nájdete varianty: Do zasklievacej
Fotonávod na vymeranie a objednanie horizontálnej žalúzie na retiazku 1. Vymeranie šírky a výšky horizontálnej žalúzie na retiazku - vymeranie sa vykonáva podľa uchytenia. Nižšie nájdete varianty: Do zasklievacej
Gem o rama Je 5-valcový, multi-líniový výherný video prístroj s desiatimi fixnými hernými líniami. Hra je prístupná aj prostredníctvom mobilnej verzie
 Gem o rama Je 5-valcový, multi-líniový výherný video prístroj s desiatimi fixnými hernými líniami. Hra je prístupná aj prostredníctvom mobilnej verzie, pričom pravidlá hry, vklady a výhry sú totožné s
Gem o rama Je 5-valcový, multi-líniový výherný video prístroj s desiatimi fixnými hernými líniami. Hra je prístupná aj prostredníctvom mobilnej verzie, pričom pravidlá hry, vklady a výhry sú totožné s
Ako vybrať hliníkové disky (elektróny)
 1. Technický popis hliníkových diskov Každý disk je označený kódom, podľa ktorého sa dá identifikovať a porovnať s technickými údajmi vo Vašom technickom preukaze: 8J x 16", 4/100, ET30 8 - Šírka disku
1. Technický popis hliníkových diskov Každý disk je označený kódom, podľa ktorého sa dá identifikovať a porovnať s technickými údajmi vo Vašom technickom preukaze: 8J x 16", 4/100, ET30 8 - Šírka disku
Sprievodný list SofComs.r.o., Priemyselná 1, Liptovský Mikuláš Program basic.sk Verzia ( ) Dátum Autor Ing. J. Malíček
 Sprievodný list SofComs.r.o., Priemyselná 1, 031 01 Liptovský Mikuláš Program basic.sk Verzia 3.01.11 (3.02.01) Dátum 20.12.2017 Autor Ing. J. Malíček, Z. Patka Hot - line 044/562 41 97-8 Vážený používateľ
Sprievodný list SofComs.r.o., Priemyselná 1, 031 01 Liptovský Mikuláš Program basic.sk Verzia 3.01.11 (3.02.01) Dátum 20.12.2017 Autor Ing. J. Malíček, Z. Patka Hot - line 044/562 41 97-8 Vážený používateľ
03_ControlFlow.dvi
 1 Riadenie toku programu Príkazy v Matlabe na kontrolu toku programu fungujú veľmi podobne ako v iných programovacích jazykoch. Zoznam: IF (IF-END, IF-ELSE-END, IF-ELSEIF-ELSE-END), SWITCH-CASE, FOR cykly,
1 Riadenie toku programu Príkazy v Matlabe na kontrolu toku programu fungujú veľmi podobne ako v iných programovacích jazykoch. Zoznam: IF (IF-END, IF-ELSE-END, IF-ELSEIF-ELSE-END), SWITCH-CASE, FOR cykly,
Microsoft Word - Algoritmy a informatika-priesvitky02.doc
 3. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi základné formálne prostriedky
3. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi základné formálne prostriedky
Xesar Softvér Stručný návod
 Xesar Softvér Stručný návod Pridanie osoby Nový zamestnanec nastupuje do firmy Povinné polia treba bezpodmienečne vyplniť (meno a priezvisko) Prideľte osobe podľa potreby oprávnenie pre Manuálne trvalé
Xesar Softvér Stručný návod Pridanie osoby Nový zamestnanec nastupuje do firmy Povinné polia treba bezpodmienečne vyplniť (meno a priezvisko) Prideľte osobe podľa potreby oprávnenie pre Manuálne trvalé
FAQ
 Import skladových kariet Potrebujete si preniesť do programu OMEGA zoznam skladových kariet, prípadne nový cenník z Excelu? Vyžite funkciu importu skladových kariet: V menu Sklad Skladové karty potvrdíme
Import skladových kariet Potrebujete si preniesť do programu OMEGA zoznam skladových kariet, prípadne nový cenník z Excelu? Vyžite funkciu importu skladových kariet: V menu Sklad Skladové karty potvrdíme
Detektor kovu, napätia a dreva 3 v 1 DM-902 Každé kopírovanie, reprodukovanie a rozširovanie tohto návodu vyžaduje písomný súhlas firmy Transfer Multi
 Detektor kovu, napätia a dreva 3 v 1 DM-902 Každé kopírovanie, reprodukovanie a rozširovanie tohto návodu vyžaduje písomný súhlas firmy Transfer Multisort Elektronik. Návod na obsluhu Tento prístroj využíva
Detektor kovu, napätia a dreva 3 v 1 DM-902 Každé kopírovanie, reprodukovanie a rozširovanie tohto návodu vyžaduje písomný súhlas firmy Transfer Multisort Elektronik. Návod na obsluhu Tento prístroj využíva
GEODETICKÝ A KARTOGRAFICKÝ ÚSTAV BRATISLAVA Chlumeckého 4, Bratislava II Obsah 1. Export údajov ZBGIS do CAD formá
 GEODETICKÝ A KARTOGRAFICKÝ ÚSTAV BRATISLAVA Chlumeckého 4, 827 45 Bratislava II www.gku.sk, www.geoportal.sk Obsah 1. Export údajov ZBGIS do CAD formátu (DGN, DXF) pomocou Konverznej služby... 2 Konverzia
GEODETICKÝ A KARTOGRAFICKÝ ÚSTAV BRATISLAVA Chlumeckého 4, 827 45 Bratislava II www.gku.sk, www.geoportal.sk Obsah 1. Export údajov ZBGIS do CAD formátu (DGN, DXF) pomocou Konverznej služby... 2 Konverzia
Manuál pre nastavenie tlače z VRP Bluetooth, USB tlačiarne Bluetooth, USB tlačiarne Manuál pre nastavenie tlače -1-
 Bluetooth, USB tlačiarne Manuál pre nastavenie tlače -1- Návod pre užívateľa Platnosť licencie: VRP licencia je viazaná na DKP firmy (daňový kód pokladnice pridelený finančnou správou). Jednu licenciu
Bluetooth, USB tlačiarne Manuál pre nastavenie tlače -1- Návod pre užívateľa Platnosť licencie: VRP licencia je viazaná na DKP firmy (daňový kód pokladnice pridelený finančnou správou). Jednu licenciu
2_detsky pesibus v Novakoch_Putiska Ivan
 Ivan Putiška Nováky PEŠIBUS Je to PEŠIBUS ekologický, bezpečný, rýchly, nenáročný a lacný spôsob dopravy. V PEŠIBUSE každé ráno pešo odprevadí do školy skupinu detí jeden dospelý vodič PEŠIBUSU /rodič
Ivan Putiška Nováky PEŠIBUS Je to PEŠIBUS ekologický, bezpečný, rýchly, nenáročný a lacný spôsob dopravy. V PEŠIBUSE každé ráno pešo odprevadí do školy skupinu detí jeden dospelý vodič PEŠIBUSU /rodič
(Manu\341l)
 Manuál práce so systémom kampane DPNB 1. Základné rozdelenie záložiek v konte súťažiaceho: 1. Súhrn nájdete v ňom zosumarizované informácie o vašich jazdách, celkovom poradí na Slovensku aj v meste, ušetrenom
Manuál práce so systémom kampane DPNB 1. Základné rozdelenie záložiek v konte súťažiaceho: 1. Súhrn nájdete v ňom zosumarizované informácie o vašich jazdách, celkovom poradí na Slovensku aj v meste, ušetrenom
